Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лекция 7. Геометрическое решение задач линейного программирования. Основные теоремы линейного программирования. Симплекс метод для решения задач линейного программирования.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Если система ограничений задачи линейного программирования представлена в виде системы линейных неравенств с двумя переменными, то такая задача может быть решена геометрически. Таким образом, данный метод решения ЗЛП имеет очень узкие рамки применения. Однако метод представляет большой интерес с точки зрения выработки наглядных представлений о сущности задач линейного программирования. Геометрический (или графический) метод предполагает последовательное выполнение ряда шагов. Ниже представлен порядок решения задачи линейного программирования на основе ее геометрической интерпретации. 1. Сформулировать ЗЛП. 2. Построить на плоскости {х1, х2} прямые, уравнения которых получаются в результате замены в ограничениях знаков неравенств на знаки точных равенств. 3. Найти полуплоскости, определяемые каждым из ограничений задачи. 4. Найти область допустимых решений. 5. Построить прямую c1x1 + c2x2 = h, где h - любое положительное число, желательно такое, чтобы проведенная прямая проходила через многоугольник решений. 6. Перемещать найденную прямую параллельно самой себе в направлении увеличения (при поиске максимума) или уменьшения (при поиске минимума) целевой функции. В результате, либо отыщется точка, в которой целевая функция принимает максимальное (минимальное) значение, либо будет установлена неограниченность функции на множестве решений. 7. Определить координаты точки максимума (минимума) функции и вычислить значение функции в этой точке. Далее рассмотрим пример решения ЗЛП графическим методом. Для этого воспользуемся представленной выше задачей о хоккейных клюшках и шахматных наборах.
1. Выше уже приводилась формулировка задачи, здесь нам остается лишь повторить ее:
2. Теперь построим прямые, соответствующие каждому из функциональных ограничений задачи. Эти прямые обозначены на рисунке (1), (2) и (3).
3. Штрихи на прямых указывают полуплоскости, определяемые ограничениями задачи. 4. Область допустимых решений включает в себя точки, для которых выполняются все ограничения задачи. В нашем случае область представляет собой пятиугольник (на рисунке обозначен ABCDO и окрашен синим цветом).
5. Прямая, соответствующая целевой функции, на рисунке представлена пунктирной линией. 6. Прямую передвигаем параллельно самой себе вверх (направление указано стрелкой), поскольку именно при движении в этом направлении значение целевой функции увеличивается. Последней точкой многоугольника решений, с которой соприкоснется передвигаемая прямая, прежде чем покинет его, является точка C. Это и есть точка, соответствующая оптимальному решению задачи. 7. Осталось вычислить координаты точки С. Она является точкой пересечения прямых (1) и (2). Решив совместно уравнения этих прямых, найдем: Таким образом, для максимизации прибыли компании следует ежедневно выпускать 24 клюшки и 4 набора. Реализация такого плана обеспечит ежедневную прибыль в размере $64.
Для обоснования методов решения задач линейного программирования сформулируем ряд важнейших теорем, опуская их аналитические доказательства. Уяснить смысл каждой из теорем поможет понятие о геометрической интерпретации решения ЗЛП, данное в предыдущем подразделе. Однако сначала напомним о некоторых понятиях, важных с точки зрения дальнейшего разговора. Любые m переменных системы m линейных уравнений с n переменными (m < n) называются основными, если определитель матрицы коэффициентов при них отличен от нуля. Тогда остальные m-n переменных называются неосновными (или свободными). Базисным решением системы m линейных уравнений c n переменными (m < n) называется всякое ее решение, в котором все неосновные переменные имеют нулевые значения. Теорема 1. Множество всех допустимых решений системы ограничений задачи линейного программирования является выпуклым. В частном случае, когда в систему ограничений входят только две переменные x1 и x2, это множество можно изобразить на плоскости. Так как речь идет о допустимых решениях (x1, x2 ≥ 0), то соответствующее множество будет располагаться в первой четверти декартовой системы координат. Это множество может быть замкнутым (многоугольник), незамкнутым (неограниченная многогранная область), состоять из единственной точки и, наконец, система ограничений-неравенств может быть противоречивой.
Теорема 2. Если задача линейного программирования имеет оптимальное решение, то оно совпадает с одной (двумя) из угловых точек множества допустимых решений. Из теоремы 2 можно сделать вывод о том, что единственность оптимального решения может нарушаться, причем, если решение не единственное, то таких оптимальных решений будет бесчисленное множество (все точки отрезка, соединяющего соответствующие угловые точки). Теорема 3. Каждому допустимому базисному решению задачи линейного программирования соответствует угловая точка области допустимых решений, и наоборот. Следствием из теорем 2 и 3 является утверждение о том, что оптимальное решение (оптимальные решения) задачи линейного программирования, заданной (или приведенной) ограничениями-уравнениями, совпадает с допустимым базисным решением (допустимыми базисными решениями) системы ограничений. Таким образом, оптимальное решение ЗЛП следует искать среди конечного числа допустимых базисных решений. Симплекс-метод был разработан и впервые применен для решения задач в 1947 г. американским математиком Дж. Данцигом. Симплексный метод в отличие от геометрического универсален. С его помощью можно решить любую задачу линейного программирования. В основу симплексного метода положена идея последовательного улучшения получаемого решения. Геометрический смысл симплексного метода состоит в последовательном переходе от одной вершины многогранника ограничений к соседней, в которой целевая функция принимает лучшее (или, по крайней мере, не худшее) значение до тех пор, пока не будет найдено оптимальное решение - вершина, где достигается оптимальное значение функции цели (если задача имеет конечный оптимум). Таким образом, имея систему ограничений, приведенную к канонической форме (все функциональные ограничения имеют вид равенств), находят любое базисное решение этой системы, заботясь только о том, чтобы найти его как можно проще. Если первое же найденное базисное решение оказалось допустимым, то проверяют его на оптимальность. Если оно не оптимально, то осуществляется переход к другому, обязательно допустимому базисному решению. Симплексный метод гарантирует, что при этом новом решении целевая функция, если и не достигнет оптимума, то приблизится к нему (или, по крайней мере, не удалится от него). С новым допустимым базисным решением поступают так же, пока не отыщется решение, которое является оптимальным. Процесс применения симплексного метода предполагает реализацию трех его основных элементов: 1) способ определения какого-либо первоначального допустимого базисного решения задачи; 2) правило перехода к лучшему (точнее, не худшему) решению; 3) критерий проверки оптимальности найденного решения. Симплексный метод включает в себя ряд этапов и может быть сформулирован в виде четкого алгоритма (четкого предписания о выполнении последовательных операций). Это позволяет успешно программировать и реализовывать его на ЭВМ. Задачи с небольшим числом переменных и ограничений могут быть решены симплексным методом вручную. Далее рассмотрим симплексный алгоритм, не углубляясь в его обоснование. Реализация симплекс-алгоритма включает восемь шагов. Опишем их, параллельно рассматривая пример выполнения каждого шага в применении к задаче о хоккейных клюках и шахматных наборах.
Шаг 1. Формулировка ЗЛП (формирование целевой функции и системы ограничений). Для определенности будем считать, что решается задача на отыскание максимума. Ниже приведем общую постановку такой задачи.
Еще раз повторим формулировку задачи из нашего примера.
Шаг 2. Приведение задачи к канонической форме (перевод функциональных ограничений в систему уравнений). Для реализации шага в ограничения задачи вводятся дополнительные переменные. Ниже приведен порядок выполнения этой операции.
Обозначим добавочные переменные несколько иначе, а именно: y1 = xn+1, y2 = xn+2,..., ym = xn+m, где n - число переменных в исходной задаче, m - число уравнений. Все дополнительные переменные также должны быть неотрицательными. В отношении добавочных переменных нужно сделать еще одно важное замечание. Все они должны иметь тот же знак, что и свободные члены системы ограничений. В противном случае используется так называемый M-метод (метод искусственного базиса). Выполним второй шаг для нашего примера.
Шаг 3. Построение исходной симплекс-таблицы (получение первоначального допустимого базисного решения). При ручной реализации симплексного метода удобно использовать так называемые симплексные таблицы. Исходная симплекс-таблица соответствует первоначальному допустимому базисному решению. В качестве такового проще всего взять базисное решение, в котором основными являются дополнительные переменные xn+1, xn+2,..., xn+m. Ниже приведены исходная симплексная таблица в общем виде и в применении к рассматриваемой нами задаче. Таблица 1. Общий вид исходной симплекс-таблицы
Итак, в левом столбце записываются основные (базисные) переменные, в первой строке таблицы перечисляются все переменные задачи. Крайний правый столбец содержит свободные члены системы ограничений b1, b2,..., bm. В последней строке таблицы (она называется оценочной) записываются коэффициенты целевой функции, а также значение целевой функции (с обратным знаком) при текущем базисном решении (
Таблица 2. Исходная симплекс-таблица для задачи о хоккейных клюшках и шахматных наборах
Таким образом, в данном базисном решении неосновные переменные x1 и x2 равны нулю. Базисные переменные отличны от нуля: x3 = 120, x4 = 72, x5 = 10. Данное базисное решение является допустимым. Естественно, что значение целевой функции в этом случае равно нулю, так как в формировании целевой функции участвуют переменные, которые для данного базисного решения являются неосновными. Шаг 4. Проверка условия: все cj ≤ 0. Если НЕТ - осуществляется переход к шагу 5, если ДА - задача решена. Таким образом, на данном шаге проверяется наличие положительных элементов в последней строке симплексной таблицы. Если такие элементы имеются, необходимо продолжать решение. В нашей задаче последняя строка содержит два положительных элемента, следовательно, необходимо перейти к шагу 5. Шаг 5. Выбор разрешающего столбца (переменной, вводимой в базис). Разрешающий столбец выбирается в соответствии со следующим условием:
где r - номер разрешающего столбца. Таким образом, при определении разрешающего столбца просматривается последняя строка симплексной таблицы и в ней отыскивается наибольший положительный элемент. В нашей задаче в качестве разрешающего выберем второй столбец (соответствующий переменной x2), поскольку в последней строке для этого столбца содержится 4. Шаг 6. Проверка условия: все air ≤ 0. Если ДА - целевая функция неограничена и решения нет, если НЕТ - переход к шагу 7. Таким образом, необходимо проверить элементы разрешающего столбца. Если среди них нет положительных, то задача неразрешима. В нашем примере все элементы разрешающего столбца положительны (6, 6 и 1), следовательно, необходимо перейти к шагу 7. Шаг 7. Выбор разрешающей строки (переменной, выводимой из базиса) по условию:
где s - номер разрешающей строки. Таким образом, для тех строк, где элементы разрешающего столбца положительны, необходимо найти частное от деления элемента bi (последний столбец таблицы) на элемент, находящийся в разрешающем столбце. В качестве разрешающей выбирается строка, для которой результат такого деления будет наименьшим. Проиллюстрируем выполнение шага 7, обратившись к нашему примеру. Для первой строки: D1 = 120 / 6 = 20. Для второй строки: D2 = 72 / 6 = 12. Для третьей строки: D3 = 10 / 1 = 10. Наименьший результат деления - в третьей строке, значит именно эту строку мы выбираем в качестве разрешающей, т.е. исключать из базисного решения будем переменную x5. Элемент, стоящий на пересечении разрешающей строки и разрешающего столбца, называется разрешающим элементом. В нашем случае таковым является единица, стоящая на пересечении третьей строки и второго столбца.
Исходная симплекс-таблица нашего примера с выделенными цветом разрешающей строкой и разрешающим столбцом представлена ниже (таблица 3). Таблица 3. Исходная симплекс-таблица с выделенными разрешающей строкой и столбцом, а также с иллюстрацией к применению правила прямоугольника
Шаг 8. Пересчет элементов симплекс-таблицы (переход к новому базисному решению). Порядок пересчета различных элементов таблицы несколько отличается. Для элементов разрешающей строки используются следующие формулы:
где s - номер разрешающей строки, r - номер разрешающего столбца,
asj, bs - старые значения пересчитываемых элементов, asr - старое значение разрешающего элемента. Таким образом, при пересчете элементов разрешающей строки каждый ее элемент делится на разрешающий элемент. Еще проще пересчитать элементы разрешающего столбца. Все они (кроме разрешающего элемента) становятся равными нулю:
Элементы, не принадлежащие разрешающим столбцу и строке, пересчитываются по так называемому правилу прямоугольника: мысленно выделяется прямоугольник, в котором элемент, подлежащий пересчету и разрешающий элемент образуют одну из диагоналей. Формулы будут иметь следующий вид:
где aij, bi, cj, L - старые значения пересчитываемых элементов. Применение правила прямоугольника проиллюстрируем, используя таблицу 3. Пересчитаем элемент a11 (в исходной симплекс-таблице его значение равно 4). В таблице 2.6 можно видеть прямоугольник (прочерчен пунктиром), соединяющий четыре элемента, участвующих в пересчете:
Аналогичным образом пересчитываются остальные элементы. По окончании пересчета осуществляется возврат к шагу 4. Полностью результат пересчета для нашего примера можно видеть в таблице 3. Таблица 3. Симплекс-таблица для задачи о хоккейных клюшках и шахматных наборах (второе базисное решение)
Таким образом, в новом базисном решении базисными переменными являются: x2 = 10, x3 = 60, x5 = 12 (соответствующие значения можно видеть в последнем столбце таблицы). Неосновные переменные x1 и x5 равны нулю. Значение целевой функции в этом случае равно 40 (значение можно видеть в правой нижней ячейке таблицы). Доведем решение нашего примера до конца. Вернемся к шагу 4 симплекс-алгоритма. Рассмотрим последнюю строку таблицы 3. В ней есть положительные элементы, значит полученное решение не является оптимальным. Шаг 5. Выберем разрешающий столбец. Им окажется столбец x1, поскольку здесь содержится единственный положительный элемент нижней строки. Стало быть, переменную x1 будем переводить в основные. Далее. Шаг 6. Проверка показывает, что в разрешающем столбце есть положительные элементы, следовательно, можно продолжать решение. Шаг 7. Определим разрешающую строку. При этом будем рассматривать лишь первую и вторую строки, поскольку для третьей строки в разрешающем столбце находится нуль. Найдем частное от деления элемента bi на элемент, находящийся в разрешающем столбце: Для первой строки: D1 = 60 / 4 = 15. Для второй строки: D2 = 12 / 2 = 6. Наименьший результат деления - во второй строке, значит именно эту строку мы выбираем в качестве разрешающей, т.е. переводить в неосновные (исключать из базиса) будем переменную x4. Ниже приведена симплекс-таблица с выделенными разрешающей строкой и столбцом (таблица 4). Таблица 4. Симплекс-таблица (второе базисное решение) с выделенными разрешающей строкой и столбцом
Далее перейдем к шагу 8 и осуществим пересчет элементов симплексной таблицы в соответствии с правилами, приводимыми выше. Результат пересчета представлен в таблице 5. Таблица 5. - Симплекс-таблица для задачи о хоккейных клюшках и шахматных наборах (третье базисное решение)
Таким образом, в очередном (третьем) базисном решении основными переменными являются: x1 = 6, x2 = 10, x3 = 36. Неосновные переменные x4 и x5 равны нулю. Значение целевой функции для этого решения равно 52. Вернемся к шагу 4 симплекс-алгоритма. Рассмотрим последнюю строку таблицы 5. В ней все еще есть положительные элементы, значит полученное решение не является оптимальным, и необходимо продолжить выполнение симплекс-алгоритма. Шаг 5. Выберем разрешающий столбец. Им окажется столбец x5, поскольку здесь содержится единственный положительный элемент нижней строки. Переменную x5 будем переводить в основные. Шаг 6. Проверка показывает, что в разрешающем столбце есть положительные элементы, следовательно, можно продолжать решение. Шаг 7. Определим разрешающую строку. При этом будем рассматривать лишь первую и третью строки, поскольку для второй строки в разрешающем столбце находится отрицательное число. Найдем частное от деления элемента bi на элемент, находящийся в разрешающем столбце: Для первой строки: D1 = 36 / 6 = 6. Для третьей строки: D2 = 10 / 1 = 10. Наименьший результат деления - в первой строке, значит именно эту строку мы выбираем в качестве разрешающей, т.е. переводить в неосновные (исключать из базиса) будем переменную x3. Ниже приведена симплекс-таблица с выделенными разрешающей строкой и столбцом (таблица 6). Таблица 6. Симплекс-таблица (третье базисное решение) с выделенными разрешающей строкой и столбцом
Далее перейдем к шагу 8 и осуществим пересчет элементов симплексной таблицы в соответствии с правилами, приводимыми выше. Результат пересчета представлен в таблице 7. Таблица 7. - Симплекс-таблица для задачи о хоккейных клюшках и шахматных наборах (четвертое базисное решение)
Таким образом, в очередном (четвертом) базисном решении основными переменными являются: x1 = 24, x2 = 4, x5 = 6. Неосновные переменные x3 и x4 равны нулю. Значение целевой функции для этого решения равно 64. Вернемся к шагу 4. Рассмотрим последнюю строку таблицы 7. Положительных элементов в ней не осталось, следовательно полученное решение является оптимальным. Решение задачи найдено. Оно, что естественно, совпадает с решением, полученным для этой же задачи при помощи графического метода:
Далее приведена общая схема симплексного алгоритма, наглядно показывающая порядок его реализации.
Лекция 8. Основные понятия и определения теории игр
Наибольшее распространение в технических приложениях имеют парные стратегические бескоалиционные конечные некооперативные игры. Модель проблемной ситуации в этом случае имеет вид: < U, V, W1, W2, R1, R2 >, где U - множество стратегий оперирующей стороны (конструктора); V - множество стратегий оппонирующей стороны (технолог и природа); W1 и W2 - показатели качества игроков; R1 и R2 - системы предпочтения игроков. Системы предпочтения игроков, в свою очередь, основываются на двух ведущих принципах рационального поведения: принципе наибольшего гарантированного результата и принципе равновесия. Первый основан на том, что рациональным выбором одного из игроков должен считаться такой, при котором он рассчитывает на самую неблагоприятную для него реакцию со стороны другого игрока. Второй принцип гласит, что рациональным выбором любого игрока считается такая стратегия u$ (или v$), для которой ситуация (u$, v$) обоюдовыгодна: любое отклонение от данной ситуации игры не является выгодным ни для одного из игроков. Классификацию игр можно проводить: по количеству игроков, количеству стратегий, характеру взаимодействия игроков, характеру выигрыша, количеству ходов, состоянию информации и т.д. В зависимости от количества игроков различают игры двух и n игроков. Первые из них наиболее изучены. Игры трёх и более игроков менее исследованы из-за возникающих принципиальных трудностей и технических возможностей получения решения. Чем больше игроков - тем больше проблем. По количеству стратегий игры делятся на конечные и бесконечные. Если в игре все игроки имеют конечное число возможных стратегий, то она называется конечной. Если же хотя бы один из игроков имеет бесконечное количество возможных стратегий игра называется бесконечной. По характеру взаимодействия игры делятся на: 1) бескоалиционные: игроки не имеют права вступать в соглашения, образовывать коалиции; 2) коалиционные (кооперативные) – могут вступать в коалиции. В кооперативных играх коалиции наперёд определены. По характеру выигрышей игры делятся на: игры с нулевой суммой (общий капитал всех игроков не меняется, а перераспределяется между игроками; сумма выигрышей всех игроков равна нулю) и игры с ненулевой суммой. По виду функций выигрыша игры делятся на: матричные, биматричные, непрерывные, выпуклые, сепарабельные, типа дуэлей и др. Матричная игра – это конечная игра двух игроков с нулевой суммой, в которой задаётся выигрыш игрока 1 в виде матрицы (строка матрицы соответствует номеру применяемой стратегии игрока 2, столбец – номеру применяемой стратегии игрока 2; на пересечении строки и столбца матрицы находится выигрыш игрока 1, соответствующий применяемым стратегиям). Для матричных игр доказано, что любая из них имеет решение и оно может быть легко найдено путём сведения игры к задаче линейного программирования. Биматричная игра – это конечная игра двух игроков с ненулевой суммой, в которой выигрыши каждого игрока задаются матрицами отдельно для соответствующего игрока (в каждой матрице строка соответствует стратегии игрока 1, столбец – стратегии игрока 2, на пересечении строки и столбца в первой матрице находится выигрыш игрока 1, во второй матрице – выигрыш игрока 2.) Для биматричных игр также разработана теория оптимального поведения игроков, однако решать такие игры сложнее, чем обычные матричные. Непрерывной считается игра, в которой функция выигрышей каждого игрока является непрерывной в зависимости от стратегий. Доказано, что игры этого класса имеют решения, однако не разработано практически приемлемых методов их нахождения. Если функция выигрышей является выпуклой, то такая игра называется выпуклой. Для них разработаны приемлемые методы решения, состоящие в отыскании чистой оптимальной стратегии (определённого числа) для одного игрока и вероятностей применения чистых оптимальных стратегий другого игрока. Такая задача решается сравнительно легко. Решается парная матричная игра (проектируемое изделие - меры и средства противодействия) с нулевой суммой (выигрыш одной стороны равен проигрышу другой) на основе рассмотрения платежной матрицы, которая представляет собой совокупность значений U и V (пара стратегий (u,v) U x V называется ситуацией игры) а также выигрышей Wij при парном сочетании всевозможных стратегий сторон.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 1333; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.123.68 (0.015 с.) |

 = 2x1 + 4x2 → max;
= 2x1 + 4x2 → max;
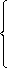

 ,
,  . Подставляя найденные величины в целевую функцию, найдем ее значение в оптимальной точке
. Подставляя найденные величины в целевую функцию, найдем ее значение в оптимальной точке  .
.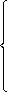

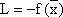 ). В рабочую область таблицы (начиная со второго столбца и второй строки) занесены коэффициенты aij при переменных системы ограничений.
). В рабочую область таблицы (начиная со второго столбца и второй строки) занесены коэффициенты aij при переменных системы ограничений.
 для air > 0,
для air > 0,



 ,
,  - новые значения пересчитываемых элементов,
- новые значения пересчитываемых элементов,
 .
.
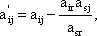


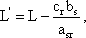
 ,
,  ,
,  ,
,  - новые значения пересчитываемых элементов,
- новые значения пересчитываемых элементов, , т.е.
, т.е.