
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 7. Подбор параметра, поиск оптимального решения. Поиск экстремума функцииСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Теоретические сведения На оглавление
При использовании финансовых функций в отдельных ячейках рабочего листа подготавливаются значения основных аргументов функции, выполняется выбор требуемой функции по Мастеру функций, через диалоговые окна которого заносятся аргументы.
Существует специфика задания значений аргументов финансовых функций: 1. Все аргументы, означающие расходы денежных средств (напр., ежегодные платежи), представляются отрицательными числами, а аргументы, означающие поступления (напр., дивиденты), - положительными числами. 2. Все даты, как аргументы, имеют числовой формат (например, 1 января 1995г. представляется числом 34700). При ссылках на ячейки с датами в последние даты записываются в обычном виде (например, 1.01.95). 3. Если не используется последний аргумент (или несколько подряд идущих), то соответствующие разделительные знаки (“;”) можно опустить.
Финансовые функции включают: ¨ функцию Цена, которая рассчитывает курс (цену) покупки ценной бумаги с периодическими выплатами купонных процентов по формуле =ЦЕНА(дата_соглашения;дата_вступления_в_силу;ставка;доход;погашение;частота; базис) ¨ функцию БC, которая производит расчет будущей или наращенной стоимости периодических постоянных платежей и будущую стоимость текущего значения вклада или займа при постоянной процентной ставке. § Если производится расчет будущей стоимости единой суммы вклада, то используют формулу § если платежи производятся систематически в начале периода, так называемые “обязательные платежи” (тип=1), используется формула =БC(норма;число_периодов;выплата;;1) § для фиксированных периодических платежей, производимых в конце периода, так называемые “обычные платежи” (тип=0), используется формула =БC(норма;число_периодов;выплата;;0) или =БC(норма;число_периодов;выплата) т.е. аргумент тип равный нулю можно опустить. Аргумент выплата означает фиксированную периодическую выплату. Аргумент нз – начальное значение вклада - берется с отрицательным знаком, что означает вложение денег. В случае выдачи денег знак аргумента нз положительный. Для задания аргументов число_периодов и норма применяется таблица 8.1, где используются параметры: n=число лет — для расчета общего числа периодов выплат (аргумент число_периодов), k=годовая процентная ставка — для расчета процента за период начисления (аргумент норма).
Таблица 8.1 Расчет аргументов функции БC
Подробную информацию о функциях и их параметрах смотрите в справочной системе Excel. Пример 8.1. С помощью функции Цена определить курс покупки ценных бумаг (облигаций), если: a) облигации приобретены (дата_соглашения) 6.09.93; b) облигации будут погашены (дата_вступления_в_силу) 12.09.97; c) размер купонной ставки (ставка) – 9% с выплатой раз в полугодие (частота = 2); d) ожидаемая годовая ставка помещения (доход) 12,57%; e) номинал облигации (погашение) 100; f) базис расчета 1 (фактический способ исчисления временного периода – год = 366 дней). Исходные данные и результаты
Пример 8.2. Рассчитать, какая сумма окажется на счете, если 27 тыс.руб. положены на 20 лет под 13,5% годовых. Проценты начисляются каждые полгода. Исходные данные и аргументы
Расчетная формула и результат
Ответ: На счете будет 368,20 тыс.руб.
Пример 8.3. Предположим, есть два варианта инвестирования средств в течение 4 лет: в начале каждого года под 26% годовых или в конце каждого года под 38% годовых. Ежегодно вносится 300 тыс.руб. Определить, сколько денег окажется на счете в конце 4-го года для каждого варианта. Исходные данные и аргументы
Расчетные формулы и результаты
Ответ: На счете окажется 2210,53 тыс. р. для 1-го варианта и 2073,74 тыс. р. для 2-го варианта. Некоторые задачи финансового анализа требуют вычислений величин, для которых в Excel не предусмотрены отдельные функции. В этом случае успешно применяется аппарат Excel Подбор Параметра. С его помощью можно выполнять исследование области допустимых значений аргументов или подбирать значения аргументов под заданное значение функции. При подборе параметра значение влияющей ячейки (параметра) изменяется до тех пор, пока формула, зависящая от этой ячейки, не возвратит заданное значение. Установив курсор в ячейку (C11), содержащую формулу с финансовой функцией (Цена), выполнить команду Данные ® Работа с данными®Анализ что-если®Подбор параметра. В появляющееся диалоговое окно (рис. 8.1) задается требуемое значение функции (желаемая или заданная ЦЕНА), а в поле “Изменяя значение ячейки” указывается адрес подбираемого аргумента (один из параметров исходных данных, например, по адресу $C$5 - СТАВКА).
Рис. 8.1. Диалоговое окно Подбор параметра В Excel можно проводить исследование влияния некоторых исходных данных, принимающих различные значения, на результирующую функцию, т.е. проводить вариантныефинансовые расчеты. Это делается с помощью Диспетчера сценариев. Сценарий – именованная совокупность значений изменяемых ячеек, в которые вводятся различные значения аргументов. При работе со сценариями следует присвоить имена ячейкам с исходными данными, которые будут “варьироваться”. Например, для аргументов финансовой функции ЦЕНА ячейкам с исходными данными присвойте имена: $B$5 – Ставка, $B$6 – Доход, $B$8 – Частота, а ячейке-результату $B$10 – Цена. Установите курсор на любую ячейку рабочего листа. Команда Данные ® Работа с данными®Анализ что-если®® Диспедчер сценариев вызывает диалоговое окно Диспетчера сценариев для создания, редактирования, объединения, удаления и просмотра созданных сценариев расчета. Новый сценарий создается кнопкой Добавить, появляется окно Добавление сценария (рис. 8.2), в котором название сценария задается в соответствующем поле, например 1. Поле Изменяемые ячейки заполняется с использованием клавиши CTRL, выделяя на рабочем листе ячейки, значения которых будут изменяться.
Рис. 8.2. Создание нового сценария Так готовятся аргументы, и после нажатия кнопки ОК, выполняются вариантные расчеты для различных вводимых значений (рис. 8.3). Кнопка Добавить переводит на предыдущее окно для создания нового сценария, а кнопка ОК – на окно, в котором можно увидеть список всех сценариев и перейти на создание отчета.
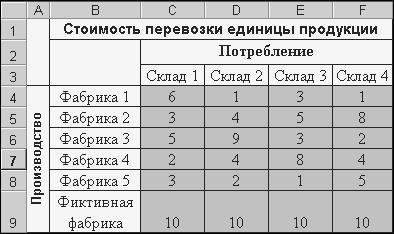
Рис. 8.3. Задание значений изменяемым ячейкам сценария Эти действия повторяются для каждого нового сценария. Все итоги сценариев можно собрать в табличный отчет в виде структуры, содержащий для каждого сценария состав изменяемых ячеек и значение выбранных результатных ячеек. В экономике и финансах всегда стоят задачи оптимального планирования штата сотрудников, фонда зарплаты, плана производства и рекламной деятельности. При этом всегда стоит проблема: как максимально удовлетворить потребности, соизмеряясь с возможностями. Excel решает задачи оптимизационного моделирования, требующего большого объема вычислений, используя мощный инструмент – Поиск решения (Данные – Анализ – Поиск решения). Если надстройка Поиск решения не отображается, то используя кнопку Офис откройте Параметры Excel и в Надстройках из списка Неактивные надстройки Excel выберите Поиск решения и нажмите кнопку Перейти. Принятие оптимальных решений базируется на “трех китах”: v Математическая модель (вводятся и описываются переменные и функции): Ø целевая функция или критерий оптимизации показывает, в каком смысле решение должно быть оптимальным (максимизация, минимизация или назначение заданного значения); Ø ограничения устанавливают зависимость между переменными (могут быть односторонними и двусторонними); Ø граничные условия показывают, в каких пределах могут быть значения искомых переменных в оптимальном решении; v Решение задачи на компьютере (через механизм Поиск решения); v Подготовка исходных данных (их достоверность). Пример 8.4 Имеются n пунктов производства (фабрик) и m пунктов распределения продукции (складов). Стоимость перевозки единицы продукции с i -ой фабрики на j -й склад cij приведена в таблице, где под строкой понимается фабрика, а под столбцом – склад. Кроме того, в этой таблице, в i -й строке указан объем производства на i -ой фабрике, а j -м столбце указан объем производства на j -ой фабрике (см. Таблицу 1). Необходимо составить план перевозок по доставке требуемой продукции на склады, с минимальными суммарными транспортными расходами. В данном случае задача не сбалансирована, т.е. объем производства (20+30+30+20+17=117) не равен объему потребляемой продукции (50+30+20+20=120). Для сбалансирования задачи введем дополнительно фиктивную фабрику и примем стоимость перевозки равной стоимости штрафа за недопоставку продукции (к примеру – 10), а объем перевозок – объемам недопоставок продукции на склады (в данном случае - 3). Таблица 1.
Составим математическую модель: Пусть xij –объём перевозок с i -й фабрики на j -й склад. Суммарная стоимость всех перевозок Неизвестные должны удовлетворять следующим ограничениям: 1. Объемы перевозок не могут быть отрицательными. 2. Так как модель сбалансирована, то вся продукция должна быть вывезена с фабрики, а потребности всех складов должны быть удовлетворены.
Модель: Минимизировать:
при ограничениях: где ai - объем производства на i - й фабрике, bj спрос на j -м складе.
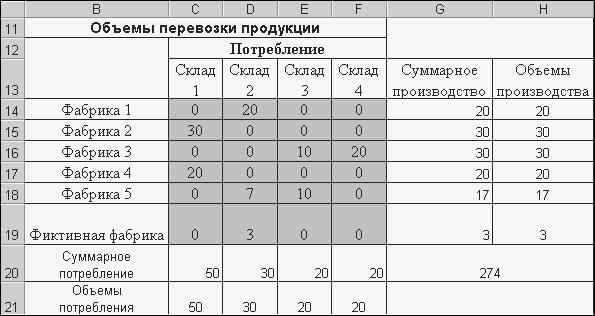
Решение. Решим данную задачу с помощью Поиска решения. Построим еще одну таблицу, которая будет заполнена объемами перевозок. Таблица 2. Таблица с исходными ячейками для ПОИСКА РЕШЕНИЯ.
Ниже вы увидите как выглядит решение этой задачи в Excel:
Рисунок 1. Данные по стоимости перевозки.
Под неизвестные отведём ячейки C14:F19, в ячейки A1:D6 введём стоимость перевозок, G14:G19 –объемы производства на фабриках, C20:F20 – потребность в продукции на складах. В ячейку G20 введём целевую функцию - =СУММПРОИЗВ(C4:F9;C14:F19).
Рисунок 2. Исходные ячейки и формулы, подготовленные для ПОИСКА РЕШЕНИЯ.
Вызовем команду поиск решения и заполним открывшееся диалоговое окно (см. рис.3). Рисунок 3. Окно ПОИСКА РЕШЕНИЯ. В параметрах поиска решения нужно установить флажок «линейная модель». Результат поиска решения (см.рис.4):
Рисунок 4. Результат ПОИСКА РЕШЕНИЯ. Анализируя полученный результат, можно видеть, что, скажем, на Склад 1 поступит 30 единиц продукции с Фабрики 2 и 20 единиц с Фабрики 4. Поскольку потребности складов превосходят мощности фабрик на 3 единицы, именно это количество продукции должно поступить на Склад 2 с фиктивной фабрики. При таком графике продукция со всех фабрик будет полностью вывезена, а потребности всех складов будут полностью удовлетворены (кроме, разумеется, Склада 2). Стоимость всех перевозок будет минимальной – 274. Практические задания На оглавление Лабораторная работа № 7 (4 часа) Цель работы: научиться использовать механизм подбора параметра и сценарный подход для проведения финансово-экономических расчетов в Excel, использовать среду Excel для поиска оптимальных решений в экономических и управленческих задачах. Задания: Загрузить шаблон Загрузить шаблон Excel_Lab_7.xltx. 1 С помощью функции Цена определить курс покупки ценных бумаг (облигаций), если: a) облигации приобретены (дата_соглашения) 01.07.96; b) облигации будут погашены (дата_вступления_в_силу) 31.12.97; c) размер купонной ставки (ставка) – 12% с выплатой раз в год (частота = 1); d) ожидаемая годовая ставка помещения (доход) 17,12%; e) номинал облигации (погашение) 100; f) базис расчета =1 2 Через Подбор параметра определить необходимый уровень ставки купона для примера из задания 1, но при условии, что облигация продается ниже номинала (погашение = 100) на 10 пунктов, т.е. по 90, при сохранении значений прочих параметров. 3. Для задачи из задания 1 построить три сценария для изменяемых параметров функции ЦЕНА и проанализировать результаты
Номера сценариев и исходные данные
4 Вклад размером 2000 тыс.руб. положен под 10% годовых. Рассчитайте, какая сумма будет на сберегательном счете через 5 лет, если проценты начисляются ежемесячно.
5 Рассчитать размер ежемесячных платежей, если был выдан кредит 50 млн.руб.на 15 лет под 14% годовых с ежемесячным начислением процентов? Поиск решения 6 Имеются n пунктов производства и m пунктов распределения продукции. Стоимости перевозок с i-го пункта в j- й центр распределения Cij приведены в таблицах (строка – пункт производства, столбец – пункт распределения). В таблице заданы объемы производств для каждого пункта производства и объемы потребления для каждого пункта распределения. Необходимо составить план перевозок продукции в пункты распределения, минимизируя суммарные транспортные расходы
7. Завод выпускает две модели радиоприемников. Для их изготовления используются отдельные технологические линии, суточный объем производства первой линии – 60 изделий, второй – 75 изделий. На радиоприемник первой модели расходуется 10 однотипных элементов электронных схем, на радиоприемник второй модели – 8 таких же элементов. Максимальный суточный запас используемых элементов равен 800 единицам. Прибыль от реализации одного приемника первой и второй моделей равен 30 и 20 долларов соответственно. Определить оптимальный суточный объем производства первой и второй моделей 8. Найти все решения системы нелинейных уравнений.
Примечание. Решение выполнить с помощью надстройки Поиск решения. Целевая фукция, например, 9. Найти max и min значения функции на отрезке х Î[4, 13]
Примечание. Предварительно необходимо построить график данной функции на отрезке х Î[4, 13]. По графику определить приближенные значения х, в которых функция имеет max и min. Решение выполнить с помощью надстройки Поиск решения. Целевая фукция Контрольные вопросы к теме 1. Каково назначение финансовых функций? Каковы их особенности? 2. Какой механизм среды Excel следует использовать, если результат для одной формулы известен, а вводимое значение нет? 3. Какая функция определяет будущий размер вклада? 4. Какие функции для работы с казначейскими обязательствами и облигациями (купонами) имеются в Excel? 5. Поясните следующие аргументы финансовых функций: цена, номинал, частота. 6. Назовите функции для расчета амортизации. 7. Опишите решение задания 6 и задания 7.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 710; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.169 (0.01 с.) |




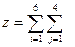 cij• xij, где cij - стоимость перевозки единицы продукции с i -й фабрики ны j -й склад.
cij• xij, где cij - стоимость перевозки единицы продукции с i -й фабрики ны j -й склад. ,
, 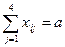 ,
,  ,
,  ,
, 



 , а в качестве ограничения вторая функция
, а в качестве ограничения вторая функция  . Изменяемые значения: x и y.
. Изменяемые значения: x и y.
 , ограничения 4 £ x £13, Изменяемые значения: x
, ограничения 4 £ x £13, Изменяемые значения: x


