
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Термодинамика гальванического элементаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Ион-дипольное взаимодействие в растворах электролитов. Сольватация и гидратация Определение реальных энергий гидратации ионов Идея метода нахождения DGs(реал) отдельного вида ионов была выдвинута А.Н.Фрумкиным и реализована Дж.Рэндлсом.
2. Ионизируем эти атомы в точке 1 вблизи поверхности металла, затратив на это работу DGион . Электроны возвращаются в металл, что дает выигрыш в энергии z 3. Ионы металла Mz+ из точки 1 переведем в точку 2. Поскольку между этими точками существует разность потенциалов VM,L, то при этом будет затрачена работа NA ze oVM,L = zF VM,L . 4. Ионы металла внесем в раствор. Соответствующий этому процессу энергетический эффект равен реальной энергии сольватации ионов DGs(реал). 5. Для завершения цикла перенесем ионы Mz+ из раствора в металл. В условиях электрохимического равновесия работа этого процесса равна нулю. При обратимом и изотермическом проведении цикла суммирование дает в согласии с законом Гесса DGсубл + DGион – z и, следовательно, DGs(реал) = – DGсубл – DGион + z Все величины в правой части этого уравнения доступны экспериментальному определению, и это открывает путь для расчета реальной энергии сольватации отдельного вида ионов. В таблице 4 приведены значения DGs(реал) для некоторых ионов, рассчитанные по наиболее надежным данным Дж. Рэндлса. Таблица 4 Опытные данные о величинах реальной энергии гидратации некоторых ионов
В литературе используется также приведенная шкала, в которой за ноль принимаются термодинамические величины для иона водорода. Расчеты любых энергий в такой шкале основаны на последовательном рассмотрении сольватации кислот и солей. Например, из свободной энергии (или энтальпии) для HCl определяют парциальные величины для хлорид-иона. Затем используют их в комбинации с данными для NaCl и определяют парциальные величины для катиона натрия и т.д. Выбор в качестве точки отсчета именно иона водорода определяется тем обстоятельством, что для него возможно относительно точное экспериментальное определение DGs(реал) методом масс-спектрометрии. Энтропия сольватации ионов Реальная и химическая энергии сольватации соли совпадают, и, суммируя величины DGs(реал) для катионов и анионов, можно получить энергию сольватации соли, а затем сопоставить ее с соответствующей теплотой сольватации. Разность DHs(соли) – DGs(соли) = TDSs(соли) позволяет рассчитать энтропии сольватации соли DSs(соли). Различия между теплотами и энергиями гидратации незначительны, что указывает на малую энтропию гидратации. Энтропии гидратации солей отрицательны. Отсюда следует, что при введении ионов структура воды становится более упорядоченной из-за ориентирующего действия ионов на ближайшие к иону диполи воды. Такой вывод подтверждается слабо выраженным и почти линейным уменьшением диэлектрической проницаемости раствора e при увеличении концентрации электролита вплоть до 0,5 – 1,0 М растворов. Дальнейшее повышение концентрации приводит к некоторому замедлению спада e и отклонению экспериментальной кривой от прямой линии в сторону больших величин e. Предполагается, что такой ход кривых e – с обусловлен наложением эффектов упорядочения структуры воды и ее разрушения под действием введенных ионов. Если рассматривать воду как систему, состоящую из квазикристаллических образований, то при введении первых порций электролита наиболее заметно проявляется их упорядочивающее действие – образование внутреннего сольватного слоя молекул воды, частичная ориентация молекул воды во внешнем сольватном слое, уменьшение свободного объема жидкости. Все эти эффекты охватывают главным образом преобладающую аморфную форму воды, связь между молекулами в которой слабее, чем в квазикристаллических образованиях, и приводит к уменьшению энтропии. При возрастании концентрации электролита, когда значительная часть аморфной воды становится связанной, в формирование гидратных оболочек вовлекаются квазикристаллические образования, их упорядоченность снижается, а энтропия возрастает. Энтропии сольватации отдельных ионов экспериментально определить невозможно. Чтобы разделить суммарные величины DSs(соли) на составляющие их энтропии DSs+ и DSs–, пользуются модельными допущениями. Наряду с чисто электростатическим, между ионами раствора и диполями растворителя возникают и другие типы ион-дипольного взаимодействия, имеющие более сложную природу. Совокупность таких взаимодействий (наиболее типичными из которых являются водородные связи), а также существенных для некоторых систем диполь-дипольных взаимодействий часто описывают в терминах донорно-акцепторных свойств растворителей. Состояние ионов в растворах В результате процесса сольватации в растворе должны присутствовать не свободные ионы, а ионы с сольватной оболочкой. Данные по энтропии сольватации, по уменьшению диэлектрической проницаемости и объема растворителя в присутствии ионов, по снижению времени релаксации, по подвижности ионов в электрическом поле указывают на то, что часть молекул растворителя довольно прочно связана с ионами. Это предположение находит прямое подтверждение в различных структурных исследованиях растворов. Бокрис и Конвей различают первичную и вторичную сольватные оболочки. Количество молекул растворителя, входящих во внутреннюю сольватную оболочку, называется числом сольватации n s (числом гидратации n г). Различные методы определения чисел сольватации приводят к значениям, существенно отличающимся друг от друга. В методе Улиха предполагается, что образование внутреннего гидратного слоя подобно замерзанию воды. Такое представление разделяют и многие другие авторы: Эли и Эванс сравнивают сольватный слой с микроскопическим айсбергом, сформировавшимся вокруг частицы растворенного вещества. Так как уменьшение энтропии при замерзании воды составляет 25,08 Дж/(К×моль), число гидратации можно оценить из соотношения: n г = – DSог / 25,08 = – 0,04 DSог . Другой метод основан на изменении диэлектрической проницаемости раствора с концентрацией электролита. Число гидратации можно также получить, измеряя сжимаемость воды и раствора. Несмотря на значительное расхождение между результатами различных методов, все они приводят к заключению об увеличении числа гидратации с уменьшением радиуса ионов и с ростом их заряда. Например, в ряду щелочных металлов эффективный радиус катиона уменьшается от лития к цезию. Предельное значение числа сольватации определяется координационным числом КЧ сольватируемого иона, то есть числом кратчайших эквивалентных связей, образуемых с молекулами растворителя без стерических затруднений. Подавляющее число катионов образует октаэдрические комплексы (КЧ = 6); для катионов малого размера КЧ = 4 (тетраэдрическое окружение); ионы сложного строения (лантаниды и актиниды) характеризуются КЧ до 12. Детальную информацию о КЧ предоставляют дифрактометрические методы. Числа сольватации не всегда совпадают с КЧ. Кроме того, наблюдается эффективное снижение чисел сольватации с ростом концентрации. Особыми закономерностями сольватации в протонных средах (в частности, в воде) характеризуются ионы гидроксония и гидроксила благодаря их способности образовывать водородные связи с растворителем, по прочности не уступающие связям между молекулами воды.
Лекция 2 Дальнейшее развитие теории Первая попытка усовершенствовать теорию Дебая и Гюккеля и расширить область ее применения была сделана самими авторами. Во втором приближении они отказались от представления об ионах как о материальных точках (допущение 3) и попытались учесть конечные размеры ионов, наделив каждый электролит некоторым средним диаметром а (при этом изменяется и допущение 4). Приписав ионам определенные размеры, Дебай и Гюккель учли тем самым силы некулоновского происхождения, препятствующие сближению ионов на расстояние, меньшее некоторой величины. Во втором приближении средний коэффициент активности описывается уравнением lg g± = - где h сохраняет прежнее значение; а условно названо средним эффективным диаметром ионов, имеет размерность длины, фактически - эмпирическая постоянная (а по своему физическому смыслу соответствует расстоянию, до которого могут сближаться электрические центры двух ионов, однако сольватация ионов делает эту величину неопределенной, и поэтому значения а подбирают, добиваясь наилучшего соответствия формулы (2) экспериментальным данным); В = c / Сохранив основные положения второго приближения теории, Гюккель учел уменьшение диэлектрической проницаемости с ростом концентрации растворов. Ее уменьшение вызывается ориентацией диполей растворителя вокруг иона, в результате чего снижается их реакция на эффект внешнего поля. Уравнение Гюккеля выглядит следующим образом: lg g± = - где С - эмпирическая константа, лишенная определенного физического смысла. При удачном подборе значений a и С формула Гюккеля хорошо согласуется с опытом и широко используется при расчетах (можно описать экспериментальные данные по g± до с порядка 1-2). При последовательном уменьшении ионной силы уравнение (3) последовательно переходит в формулу второго приближения теории Дебая и Гюккеля (уравнение (2)), а затем в предельный закон Дебая – Гюккеля (уравнение (1)). В процессе развития теории Дебая – Гюккеля и последовательного отказа от принятых допущений улучшается сходимость с опытом и расширяется область ее применимости, однако это достигается ценой превращения теоретических уравнений в полуэмпирические.
Рассмотрим рис. 4. Физической основой падения активности по сравнению с концентрацией является взаимное притяжение частиц. Взаимное отталкивание частиц в растворе должно, наоборот, вызывать увеличение активности. В разбавленных растворах электролитов электростатическое притяжение ионов оказывается преобладающим: g± < 1 и падает с ростом концентрации. Учет собственного размера ионов эквивалентен учету сил отталкивания, не позволяющих ионам сблизиться на расстояние, меньшее а. Второе приближение теории, учитывающее этот фактор, приводит к менее резкому уменьшению коэффициента активности (кривая 2) и позволяет описать опытные данные в более широком интервале концентраций. Однако в концентрированных растворах большая часть молекул воды связана ионами, так что добавление новых порций электролита должно сопровождаться разрушением сольватных оболочек и преодолением сил ион-дипольного взаимодействия. Это эквивалентно преобладанию эффекта взаимного отталкивания ионов над их взаимным притяжением; при этом g± > 1. Таким образом, переход к концентрированным растворам сопровождается резким возрастанием коэффициента активности. Чтобы описать это возрастание, в уравнение третьего приближения теории Дебая и Гюккеля и было формально введено эмпирическое слагаемое C I. Следует отметить, что зависимость коэффициента активности в разбавленных растворах электролитов от температуры оказывается весьма незначительной, поскольку повышение температуры сопровождается уменьшением диэлектрической постоянной растворителя, то есть с ростом Т произведение eТ даже несколько уменьшается. В результате при переходе от 0о к 100оС коэффициент h изменяется от 0,492 до 0,609; в 0,01 М растворе 1-1 валентного электролита это соответствует уменьшению среднего коэффициента активности всего на 2,7% (от 0,893 до 0,869). Следует учитывать, что теория дает средний рациональный коэффициент активности (g±), а экспериментальные данные для растворов обычно приводятся в шкале моляльностей (g±¢) или молярных концентраций (f ±). Средние коэффициенты активности в различных шкалах концентраций связаны следующими соотношениями: f ± = g±¢ где rL и ML – плотность и молекулярная масса чистого растворителя соответственно, M – молекулярная масса растворенного вещества, r – плотность раствора. В разбавленных растворах (с £ 0,01) g±» g±¢, но при больших концентрациях различие в значениях этих величин становится существенным. Во всех концентрационных шкалах средние коэффициенты активности при бесконечном разбавлении стремятся к 1, поскольку при этом ион-ионное взаимодействие стремится к нулю и раствор приобретает идеальные свойства. При описании растворов электролитов за стандартное состояние выбирается гипотетический раствор, в котором активности всех ионов равны единице и одновременно отсутствует ион-ионное взаимодействие (естественно, такое стандартное состояние не может быть реализовано). Существует несколько методов определения активности и коэффициентов активности электролитов. Так, например, активность соли может быть найдена по давлению пара растворителя над раствором, криоскопическим и эбуллиоскопическим методами, по осмотическому давлению. Эти методы для растворов электролитов и неэлектролитов полностью аналогичны. Кроме того, для определения активностей в растворах электролитов может быть использован метод измерения разности потенциалов на концах равновесной электрохимической цепи (метод будет рассмотрен ниже). Во всех методах измеряемые активности в тех или иных координатах экстраполируют на нулевую концентрацию, где g±¢ = 1 или f ± = 1. Активности и коэффициенты активности, полученные различными методами, совпадают в пределах точности эксперимента. Это указывает на то, что термодинамический метод описания взаимодействия в растворах электролитов является правильным и самосогласованным (вспомним, что степени диссоциации, определенные различными методами, оказывались разными). Однако термодинамический метод не раскрывает механизма взаимодействия ионов. Наиболее наглядно это проявляется в том, что при помощи термодинамического метода свойства раствора электролита можно описать как в предположении его полной диссоциации (a = 1), так и при допущении, что электролит диссоциирован лишь частично.
Раздел II. Неравновесные явления в растворах электролитов Лекция 3 Электропроводность растворов электролитов: основные понятия; связь электропроводности со свойствами электролитов и природой растворителя; влияние концентрации и температуры на электропроводность В зависимости от природы токопроводящих частиц все вещества можно условно разделить на пять групп: 1. Непроводящие тела, или изоляторы. В них даже при весьма больших электрических полях не наблюдается прохождения тока. К числу изоляторов относят обычно вещества, для которых удельное сопротивление r больше 106 Ом×м. 2. Проводники первого рода, или электронопроводящие тела. К ним относятся металлы, их некоторые оксиды и углеродистые материалы. Прохождение тока обеспечивается электронами; r лежит в пределах 10–8 – 10–5 Ом×м. Температурный коэффициент проводимости отрицателен, то есть с ростом температуры электропроводность уменьшается. 3. Полупроводники – вещества (некоторые полуметаллы, интерметаллиды, соли, органические соединения), в которых ток переносится электронами и дырками. По электропроводности они располагаются между изоляторами и металлами и их r изменяется в широких пределах (10–7 – 103 Ом×м). Температурный коэффициент электропроводности положителен. 4. Проводники второго рода, или ионные проводники. Ток переносится ионами. К ним относятся многие твердые соли (101 £ r £ 106 Ом×м), ионные расплавы (10–3 < r < 10–1 Ом×м), растворы электролитов (10–2 £ r £ 104 Ом×м). Температурный коэффициент электропроводности положителен. 5. Смешанные проводники – тела, сочетающие электронную и ионную проводимости, например, растворы щелочных и щелочноземельных металлов в жидком аммиаке, некоторые твердые соли. Их электропроводность, а также знак температурного коэффициента проводимости зависят от состава проводника и от температуры (от относительного вклада электронной и ионной составляющих), изменяясь от значений, характерных для чисто ионных проводников, до значений, присущих металлам. Предмет дальнейшего рассмотрения – преимущественно ионные проводники – растворы электролитов. Подвижность ионов Свяжем электропроводность электролита со скоростью движения его ионов в электрическом поле. По закону Ома R = U/I. Следовательно, K = I/U; I = i × S (i - плотность тока, или ток, приходящийся на 1 см2 поверхности электрода; S - площадь электрода); U = E × l (Е - напряженность поля, или падение напряжения на 1 см расстояния; l - расстояние между электродами). Тогда k При Е = 1 В/см i = k. I = Таким образом, k - это количество электричества, которое проходит в единицу времени через единицу поперечного сечения проводника при напряженности электрического поля 1 В/см. Следовательно, для вычисления электропроводности надо подсчитать число ионов, проходящих через поперечное сечение электролитического сосуда в единицу времени. Так как электричество переносится ионами различных знаков, движущимися в противоположных направлениях, то общая сила тока складывается из количеств электричества, перенесенных катионами (I+) и анионами (I–): I = I+ + I–. Введем обозначения: u¢ - скорость движения катионов (см/с); v¢ - скорость движения анионов (см/с); с ¢ - эквивалентная концентрация (г-экв/см3); S - поперечное сечение цилиндрического сосуда (см2); l - расстояние между электродами (см); U - разность потенциалов между электродами (В). Подсчитаем количество катионов, проходящих через поперечное сечение электролита в 1 секунду. За это время через сечение пройдут все катионы, находившиеся на расстоянии не более чем u¢ см от выбранного сечения, то есть все катионы в объеме u¢S: n + = u¢S c +. Так как каждый г-экв ионов несет согласно закону Фарадея F =96485 Кл электричества, то сила тока (в А) I+ = n + F = u¢S c + F. Аналогично для анионов I– = n – F = v¢S c – F. Для суммарной силы тока (предполагая, что электролит бинарный и полностью диссоциированный, так что с + = с – = с ¢): I = I+ + I– = (u¢ + v¢)S c ¢F. Скорости движения ионов u¢ и v¢ зависят от природы ионов, напряженности электрического поля U/ l, концентрации, температуры, вязкости среды и т.п. Пусть все факторы постоянны, кроме напряженности электрического поля; можно считать, что скорость ионов пропорциональна приложенной силе, то есть напряженности поля: u¢ = u где u, v - скорости ионов в стандартных условиях, то есть при напряженности поля, равной 1 В/см; они называются абсолютными подвижностями ионов и измеряются в см2/(с×В). I = (u + v) c ¢SFU/ l. По закону Ома I = U/R = U×K = U×k Отсюда k = (u + v) c ¢F, l = u×F и v×F - это скорости движения ионов, выраженные в электростатических единицах; они называются ионными электропроводностями (или просто подвижностями ионов): u×F = l+, v×F = l–. Для сильных электролитов l = l+ + l–. Для слабых электролитов с + = с ×a, с – = с ×a, l = (l+ + l–)×a. При бесконечном разведении (j ® ¥, a ® 1, с + = с – = с): l¥ = lо+ + lо– - как для сильных, так и для слабых электролитов. Величины lо+ и lо– являются предельными электропроводностями (предельными подвижностями) ионов. Они равны эквивалентным электропроводностям катиона и аниона при бесконечном разведении и измеряются в тех же единицах, что и l и l¥, то есть в см2/(Ом×г-экв). Вышеприведенное уравнение является выражением закона Кольрауша: эквивалентная электропроводность при бесконечном разведении равна сумме предельных подвижностей ионов. Таким образом, для всех электролитов можно записать lс = aс ×l¥, aс = lс / l¥. l+ и l– зависят от концентрации (разведения), особенно для сильных электролитов; lо+ и lо– - табличные величины. Все эти величины относятся к 1 г-экв ионов. Подвижность является важнейшей характеристикой ионов, отражающей их специфическое участие в электропроводности электролита. В водных растворах все ионы, за исключением ионов Н3О+ и ОН–, обладают подвижностями одного порядка; их lо составляют не более 80 см2/(Ом×г-экв) при 25оС; их абсолютные подвижности (u и v) равны нескольким см в час. Подвижности же ионов Н3О+ и ОН– составляют соответственно ~350 и ~200 см2/(Ом×г-экв). В результате эквивалентная электропроводность растворов солей выражается величинами порядка 100 – 130 см2/(г-экв×Ом). Ввиду исключительной подвижности иона гидроксония величины l¥ для кислот в 3-4 раза больше, чем для солей; щелочи занимают промежуточное положение. Рассмотрим влияние природы иона (его радиуса и заряда) на величину подвижности иона. Движение иона можно уподобить движению макроскопического шарика в вязкой среде и применить в этом случае формулу Стокса u¢ = где е - заряд электрона; z - число элементарных зарядов иона; r - эффективный радиус иона; h - коэффициент вязкости; U/ l - напряженность поля. Движущую силу - напряженность поля U/ l при вычислении абсолютных подвижностей принимаем равной единице. Следовательно, скорость движения ионов обратно пропорциональна их радиусу. Рассмотрим ряд Li+, Na+, K+ , Rb+ , Cs+ . Так как в указанном ряду истинные радиусы ионов увеличиваются, то подвижности должны уменьшаться в той же последовательности. Однако в действительности это не так. Подвижности увеличиваются при переходе от Li+ к K+ почти в два раза. Из этого можно сделать заключение, что в растворе и ионной решётке ионы обладают разными радиусами. При этом чем меньше истинный (кристаллохимический) радиус иона, тем больше его эффективный радиус в электролите. Это явление можно объяснить тем, что в растворе ионы не свободны, а гидратированы. Тогда эффективный радиус движущегося в электрическом поле иона будет определяться в основном степенью его гидратации, то есть количеством связанных с ионом молекул воды. Связь иона с молекулами растворителя ионно-дипольная, а так как напряжённость поля на поверхности иона лития гораздо больше, чем на поверхности иона калия, то степень гидратации иона лития больше степени гидратации иона калия. Таким образом, при переходе от катиона Li+ к катиону Rb + подвижность не падает, а возрастает, так как радиус гидратированного иона Li+ больше, чем радиус гидратированного иона Na+ и т.д. Однако если собственный размер иона возрастает настолько, что прочная гидратная оболочка вокруг него уже не удерживается, то при дальнейшем увеличении кристаллографического радиуса следует ожидать уменьшения подвижности. Эта закономерность наблюдается и для катионов (при переходе от Cs + к [(CH3)4N]+ ), и для анионов (при переходе от Br– к J– и далее к CH3COO– ). В ряду катионов и анионов размеры ионов Rb + , Cs + и Br– , J– являются как бы критическими: при меньших собственных размерах ионов они образуют прочную гидратную оболочку и их окончательный размер становится больше, а l i o – меньше; с другой стороны, при бόльших собственных размерах ионов они гидратированы, и l i o падает из-за увеличения собственного радиуса иона. Итак, ионы Rb + , Cs + , Br– , J– обладают наибольшей подвижностью из всех ионов, за исключением Н3О+ и ОН– . Согласно формуле Стокса многозарядные ионы должны обладать большей подвижностью, чем однозарядные. Однако скорости движения многозарядных ионов ненамного превышают скорости движения однозарядных, что объясняется большей степенью их гидратации. Термодинамика гальванического элемента Важнейшей количественной характеристикой гальванического элемента является электродвижущая сила (ЭДС, Е), которая равна разности потенциалов правильно разомкнутого элемента (такого, у которого к конечным электродам элемента присоединены проводники первого рода из одного и того же материала). Пусть в электрохимической системе обратимо и изотермически протекает реакция nA A + nB B +... ± nF Û nL L + nM M +... ± Электрическая энергия, вырабатываемая элементом, равна полезной работе А¢ суммарного процесса. Полезная работа А¢ обратимого процесса максимальна и при р,Т = const равна убыли изобарного потенциала системы -DG р ,T = n FE р ,T, где E р ,T - обратимая ЭДС системы. E р ,T = -DG р ,T / n F, EV,T = -DFV,T / n F.
Таким образом, измерив ЭДС элемента и ее температурный коэффициент, можно найти величины DG и DS для суммарного процесса, протекающего в гальваническом элементе. Этот процесс является самопроизвольным, следовательно, DG < 0. По уравнению Гиббса – Гельмгольца можно вычислить изменение энтальпии процесса: DG = DH + T DH = DG - T n FE р = - DH + n FT n FEV = - DU + n FT Из уравнений следует, что соотношение между электрической энергией, обратимо генерируемой или поглощаемой в электрохимической системе, и тепловым эффектом протекающей в ней реакции зависит от знака и величины температурного коэффициента ЭДС dE/dT: 1. Если dE/dT > 0, то n FE > При условии dE/dT > 0 химическая реакция в элементе может быть как экзотермической, так и эндотермической. Если DН < 0, то электрическая работа совершается за счет убыли энтальпии и за счет энтропийного члена 2. Если dE/dT < 0, то n FE < 3. Если dE/dT = 0, то DG = DH и n FE = Для расчета ЭДС уравнения можно переписать в виде EV = При использовании уравнений необходимо помнить, что они справедливы только для обратимых электрохимических систем, поэтому при изучении зависимости ЭДС от температуры необходимо избегать применения электрохимических систем с жидкостными границами, так как возникающие на них диффузионные потенциалы не являются равновесными. Свяжем ЭДС элемента с константой равновесия реакции, протекающей в элементе, воспользовавшись уравнением изотермы химической реакции: -DG = RT ln K a - RT E = - Первый член правой части уравнения при заданных р,Т - величина постоянная, его можно обозначить через Ео . Ео - стандартная ЭДС элемента (электрохимической системы), то есть ЭДС при всех ai = 1. Е = Ео + Таким образом, ЭДС электрохимической системы является функцией активностей участников электрохимической реакции. Вышеприведенные уравнения дают возможность вычислить величины DG и К а по экспериментальным значениям Е и, наоборот, рассчитывать Е, зная термодинамические характеристики химической реакции. Раздел I. Равновесные явления в растворах электролитов Лекция 1
|
||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 654; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.63.148 (0.02 с.) |

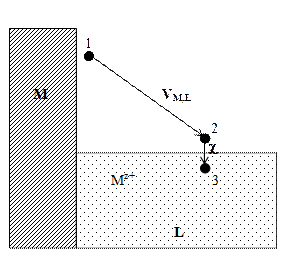 Рис. 3. Схема для расчета реальной энергии сольватации иона
Рис. 3. Схема для расчета реальной энергии сольватации иона
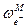 , где
, где 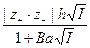 , (2)
, (2) , В незначительно изменяется с Т. Для водных растворов при 25оС произведение В а близко к 1. Формула (2) хорошо описывает поведение многих электролитов вплоть до с = 0,1 (для водных растворов NaCl при 25оС с точностью до 1-2%), однако и во втором приближении нельзя полностью описать весь диапазон зависимости g± от с. Экспериментальные значения g± при высоких концентрациях электролита начинают возрастать, и в некоторых растворах это возрастание очень значительно (в водном растворе HClO4 при m = 16 g± = 500).
, В незначительно изменяется с Т. Для водных растворов при 25оС произведение В а близко к 1. Формула (2) хорошо описывает поведение многих электролитов вплоть до с = 0,1 (для водных растворов NaCl при 25оС с точностью до 1-2%), однако и во втором приближении нельзя полностью описать весь диапазон зависимости g± от с. Экспериментальные значения g± при высоких концентрациях электролита начинают возрастать, и в некоторых растворах это возрастание очень значительно (в водном растворе HClO4 при m = 16 g± = 500).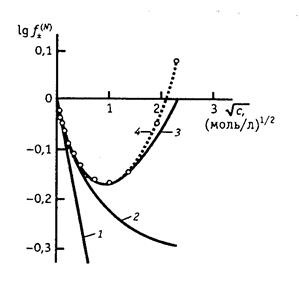
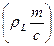 , g± = g±¢ (1 + 0,001nML m), g± = f ± [r – 0,001 с (M – ML)]×(1/rL),
, g± = g±¢ (1 + 0,001nML m), g± = f ± [r – 0,001 с (M – ML)]×(1/rL),
 =
= 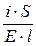 ; i = k× E.
; i = k× E.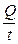 ; i =
; i =  .
.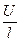 , v¢ = v
, v¢ = v  .
. ; с ¢ = с /1000; l = k/ с ¢ = (u + v)F.
; с ¢ = с /1000; l = k/ с ¢ = (u + v)F.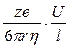 ,
,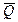 .
.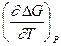 = -DS = - n F
= -DS = - n F 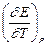 ,
, 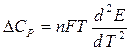 .
.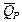 + n FT
+ n FT  =
= 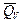 + n FT
+ n FT 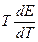 > 0. Если DН = 0, то электрическая работа совершается только за счет роста энтропии в системе. Обычный путь использования химической энергии реакции в форме выделяющегося тепла здесь невозможен, так как тепловой эффект равен нулю. Наконец, если реакция эндотермична (DН > 0), но
> 0. Если DН = 0, то электрическая работа совершается только за счет роста энтропии в системе. Обычный путь использования химической энергии реакции в форме выделяющегося тепла здесь невозможен, так как тепловой эффект равен нулю. Наконец, если реакция эндотермична (DН > 0), но  , то от гальванического элемента можно получить работу. В этих условиях за счет энтропийного фактора (то есть за счет роста энтропии системы) не только совершается электрическая работа, но и увеличивается энтальпия системы.
, то от гальванического элемента можно получить работу. В этих условиях за счет энтропийного фактора (то есть за счет роста энтропии системы) не только совершается электрическая работа, но и увеличивается энтальпия системы.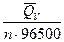 + T
+ T 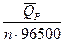 + T
+ T 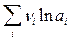 ,
,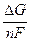 =
= 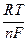 ln K a -
ln K a - 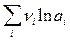 .
.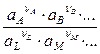 = Eo + 2,303
= Eo + 2,303 


