
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчет элементов деревянных конструкций по предельным состояниям I группыСодержание книги
Поиск на нашем сайте
Общие положения 7.1.1 Раздел применяется для расчета элементов из цельной и клееной древесины, а также клеефанерных элементов. Расчет конструкций допускается выполнять с использованием численных методов при соблюдении следующих требований: — моделирование свойств древесины производят, как транстропного материала; — для сжатых и сжато-изгибаемых элементов с гибкостью l ³ 35 расчет, как правило, выполняют по деформированной схеме; — проверку напряжений необходимо производить для наиболее опасных сечений элементов. 7.1.2 Допускается проектирование деревянных конструкций на основании испытаний, проведенных в соответствии с требованиями СТБ 1591. Центрально растянутые элементы 7.2.1 Центрально растянутые вдоль волокон элементы следует рассчитывать по формуле
где A inf — площадь поперечного сечения элемента нетто;
7.2.2 При определении A inf, ослабления, расположенные на участке длиной до 0,2 м, следует принимать совмещенными в одном сечении. 7.2.3 Растянутые элементы постоянного сечения с несимметричным ослаблением следует рассчитывать на внецентренное растяжение по формуле (7.20). 7.2.4 В сечениях элементов с равномерным растяжением поперек волокон должны соблюдаться следующие условия: s t ,90, d = Nd / Ad £ ft ,90, d — для цельной древесины; (7.2) s t ,90, d = Nd / Ad £ k 1 ∙ ft ,90, d — для клееной древесины, (7.3) где k 1 = 0,8 — коэффициент, учитывающий снижение прочности клеевого шва при растяжении поперек волокон; Nd — расчетная продольная сила; Ad — расчетная площадь поперечного сечения. Центрально сжатые элементы Элементы из цельной и клееной древесины 7.3.1 Центрально сжатые элементы постоянного поперечного сечения следует рассчитывать по формулам: на прочность
на устойчивость
где fc ,0, d — расчетное сопротивление древесины сжатию вдоль волокон; Ad — расчетная площадь поперечного сечения, принимаемая равной: — площади сечения брутто A sup, если ослабления не выходят на кромки и площадь ослабления не превышает 25 % площади брутто; — площади сечения нетто A inf с коэффициентом 4/3, если ослабления не выходят на кромки и площадь ослабления превышает 25 % площади брутто; — площади сечения нетто A inf, если ослабления выходят на кромки; kc — коэффициент продольного изгиба, определяемый по формуле (7.6) или (7.7). 7.3.2 При расчете центрально сжатых элементов на устойчивость следует учитывать упругую Коэффициент продольного изгиба следует определять по формуле (7.6) или (7.7), в зависимости от гибкости элемента:
где с = 0,8 для древесины и с = 1 для фанеры; С = 3000 для древесины и С = 2500 для фанеры. 7.3.3 Гибкость элементов цельного, постоянного по длине сечения определяется по формуле
где i — радиус инерции сечения элемента в направлении соответствующей оси. 7.3.4 Расчетную длину элемента
где l — свободная длина элемента. 7.3.5 Расчет на устойчивость центрально сжатых элементов переменного по высоте и постоянного по ширине сечения следует выполнять по формуле
где
Таблица 7.1 — Значения коэффициента kg , n для расчета сжатых и сжато-изогнутых элементов
|
||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 325; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.156.17 (0.009 с.) |

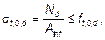
 (7.1)
(7.1) — расчетная продольная сила;
— расчетная продольная сила; — расчетное сопротивление древесины растяжению вдоль волокон.
— расчетное сопротивление древесины растяжению вдоль волокон. (7.4)
(7.4)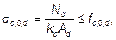 (7.5)
(7.5) = 70.
= 70.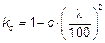 при
при 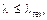 (7.6)
(7.6)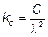 при
при 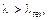 (7.7)
(7.7)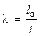 , (7.8)
, (7.8) — расчетная длина элемента;
— расчетная длина элемента; (7.9)
(7.9)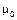 — коэффициент, определяемый в соответствии с требованиями 7.7;
— коэффициент, определяемый в соответствии с требованиями 7.7;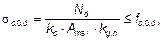 (7.10)
(7.10)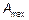 — площадь поперечного сечения брутто с максимальными размерами;
— площадь поперечного сечения брутто с максимальными размерами;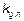 — коэффициент, учитывающий переменность высоты сечения, определяемый по таблице 7.1;
— коэффициент, учитывающий переменность высоты сечения, определяемый по таблице 7.1; — коэффициент продольного изгиба, определяемый согласно 7.3.2 для гибкости, соответствующей сечению с максимальными размерами.
— коэффициент продольного изгиба, определяемый согласно 7.3.2 для гибкости, соответствующей сечению с максимальными размерами.






