Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Модельные методы расчета энергии гидратации ионовСодержание книги
Поиск на нашем сайте
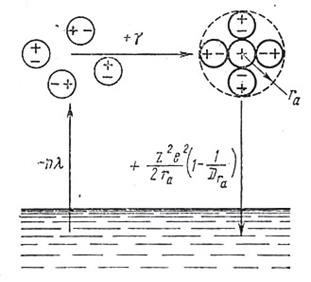
Энергия сольватации представляет собой выигрыш в энергии, который получается при перенесении моля ионов из вакуума в данный растворитель. При этом предполагается, что такой выигрыш в энергии не включает в себя электростатическое взаимодействие ионов. Чтобы избежать этого осложнения, раствор нужно поддерживать электронейтральным (вводить в него соответствующее количество ионов противоположного знака), а взаимное притяжение катионов и анионов элиминировать достаточным разбавлением раствора (теоретически бесконечным). 1. Расчет энергии и теплоты гидратации иона по методу непрерывной среды (модель Борна). Наиболее простая модель для оценки энергии сольватации была предложена М.Борном. Согласно этой модели, ион рассматривается как заряженный шарик радиуса ri, а растворитель – как сплошная однородная среда (континуум) с диэлектрической постоянной e. При неизменной плотности заряда на пластинах плоского конденсатора напряженность поля между ними оказывается большей в вакууме ЕV, чем в диэлектрике ЕD. Отношение ЕV / ЕD = e называется диэлектрической проницаемостью вещества e при условии, что проницаемость для вакуума e о принята равной единице (e о = 8,85419×10–12 Ф/м = 8,85419 пФ/м). Процесс переноса заряженного шарика из вакуума в среду разбивается на три этапа: 1. Разряд шарика в вакууме; 2. Перенос незаряженного шарика из вакуума в растворитель; 3. Заряжение шарика в среде. При этом предполагается, что работа на втором этапе А2 = 0, а для расчета работы на этапах 1 и 3 используются основные законы электростатики. Так, согласно закону Кулона, сила, действующая на каждый из двух зарядов q1 и q2, находящихся в среде с диэлектрической постоянной e на расстоянии r, равна F = Поэтому напряженность поля Е, то есть сила, которая действует на заряд +1, находящийся в среде на расстоянии r от заряда q, составляет Е = Поскольку напряженность поля связана с электрическим потенциалом j общей формулой Е = – dj / d r, то для потенциала на поверхности сферы радиуса ri получим j = – где нижний предел интегрирования соответствует выбору нулевого потенциала на бесконечно большом расстоянии от рассматриваемой сферы. Из данного уравнения вытекает следующая формула для работы заряжения сферы: А = В соответствии с этой формулой для работ А1 и А3 получаем выражения А1 = где zi e o – заряд иона. Учитывая, что свободная энергия сольватации – DGs = NA – DGs = NA Таким образом, по теории Борна энергия сольватации иона определяется его зарядом и размерами, а также диэлектрической проницаемостью растворителя. Вышеприведенное уравнение можно применять к любым растворам, если известны их диэлектрические проницаемости. Так как электролиты диссоциируют за счет энергии сольватации, то, если признать представления Борна справедливыми, диссоциирующая способность растворителя и его диэлектрическая проницаемость должны находиться между собой в прямой зависимости. Подобное соотношение было обнаружено П.И.Вальденом (1903) еще до появления теории сольватации Борна. Для ряда тетразамещенных аммония Вальденом было установлено следующее эмпирическое правило: e где Va – разведение, необходимое для достижения определенной степени диссоциации, одинаковой для всех сравниваемых растворов. Следует иметь в виду, что правило Вальдена имеет ограниченную применимость. Если воспользоваться уравнением Гиббса – Гельмгольца DH = DG – T то можно получить также выражение для теплоты сольватации: – DНs = NA Вышеприведенное уравнение называют уравнением Борна – Бьеррума. Качественно формула Борна правильно передает взаимную связь между энергиями (теплотами) сольватации и свойствами ионов. Так, в соответствии с опытом, теплоты гидратации растут с уменьшением радиуса иона и увеличением его заряда (см. выше), такой же вывод следует и из основной формулы модели Борна. Количественная проверка теории сольватации Борна (например, сравнение рассчитанных величин с величинами DНs(соли), полученными из цикла Борна – Габера) показывает, что рассчитанные величины значительно превышают соответствующие экспериментальные значения. Это указывает на весьма приближенный характер допущений, положенных в основу модели Борна. Для расчетов по формуле Борна необходимо знать диэлектрическую проницаемость растворителя и радиус иона. Радиусы ионов Борн принимал равными кристаллохимическим радиусам. Использование кристаллохимических радиусов вместо эффективных радиусов ионов в растворах приводит к ошибке при расчетах. Другая ошибка связана с отождествлением диэлектрической проницаемости раствора и чистого растворителя. Были предприняты неоднократные попытки уточнить теорию сольватации Борна. Некоторые из них проводились в рамках все того же континуального подхода. Так, Уэбб несколько усовершенствовал формулу Борна, введя в нее поправки на уменьшение диэлектрической проницаемости раствора вблизи иона и на работу сжатия растворителя при введении электролита (явление электрострикции). Учет обоих эффектов приводит к тому, что величины энергий и теплот гидратации, вычисленные по формуле Борна – Уэбба, уменьшаются и приближаются к опытным. В теории Уэбба растворитель по-прежнему рассматривается как непрерывная среда и не учитывается ни строение его молекул, ни структура жидкости. При рассмотрении процесса гидратации (сольватации) необходимо учитывать влияние каждого участника этого процесса, то есть и иона, и растворителя. Иными словами, достаточно полную картину процесса сольватации можно получить лишь тогда, когда будет выяснено, что делается с ионами при попадании их в растворитель и что происходит с растворителем в результате внесения в него ионов. Современный уровень разработки теории жидкого состояния не может дать полного и однозначного ответа на эти вопросы, хотя отдельные результаты в этом направлении уже получены. Протекание процесса сольватации определяется природой ионов (размер, заряд …), строением молекул жидкости и структурой ее в целом. Некоторые из этих факторов приняты во внимание в теории сольватации Борна – Уэбба, правда, только в виде первого приближения. Бокрис и Конвей (1954) считают, что процесс сольватации проявляется по-разному в непосредственной близости от иона и в слоях растворителя, удаленных от него, то есть в ходе сольватации возникают как бы две сольватные оболочки – внутренняя и внешняя. Внутренняя сольватная оболочка состоит из молекул растворителя, прочно связанных с ионом и перемещающихся вместе с ним при его движении. Внешняя сольватная оболочка включает в себя все молекулы растворителя, состояние которых отличается от их состояния в исходном растворителе. В соответствии с этим различают первичную и вторичную энергии сольватации. Основной вклад в общую энергию сольватации дает энергия, отвечающая образованию внутренней сольватной оболочки. Предложенные до настоящего времени модельные методы расчета используют либо различные представления о строении молекул воды, либо исходят из различных представлений о воде как о жидкой фазе. 2. Метод Ван-Аркеля и де-Бура был одним из первых модельных методов расчета энергии гидратации (1928). Они предложили расчленить энергию гидратации на две компоненты, одна из которых соответствует энергии образования первого гидратного слоя, а другая – дальнейшему процессу гидратации. Энергию гидратации они рассчитывали при помощи следующего цикла (см. рис. 1): 1. Испаряется n молекул воды, необходимых для образования первого гидратного слоя (n принимается равным 4, 6 или 8). На этот процесс расходуется энергия n l (где l – теплота испарения одной молекулы воды). 2. Испарившиеся n молекул воды реагируют в газовой фазе с ионом, образуя гидратированный ион с радиусом r a; при этом выделяется энергия g. Она слагается из энергии взаимодействия диполей с ионом, энергии притяжения и отталкивания диполей, энергии наведения индуцированных диполей и борновской энергии отталкивания. 3. Образовавшийся комплекс радиуса r a (r a = r + 2 r w , где r – кристаллохимический радиус иона, а r w – радиус молекулы воды) вносится в раствор. Выделяющаяся энергия рассчитывается по формуле Борна – Уэбба – DGs = NA Энергия гидратации равна сумме всех частных энергетических эффектов: – DGs = NA [ – n l + g + Эта формула дает лучшую сходимость с опытом, чем формула Борна. Метод Ван-Аркеля и де-Бура отличается от борновского тем, что в нём процесс гидратации разделяется на два этапа. Энергия образования первого гидратного слоя вычисляется на основе взаимодействия между газообразным ионом и полярными молекулами воды, то есть взаимодействия, происходящего вне сферы жидкой фазы. Такой способ расчёта позволяет учесть свойства отдельных молекул воды (их дипольные моменты, поляризуемость и т.п.). Поэтому при рассмотрении процесса образования первого гидратного слоя, где эти свойства особенно важны, появляется возможность отказаться от представления о воде лишь как о среде с определённой диэлектрической проницаемостью. На второй стадии цикла в воду вносится ион, уже частично гидратированный, с радиусом значительно большим, чем радиус исходного иона. Возмущения, вызванные введением такого гидратированного иона в воду, будут меньшими, и представление о воде как о непрерывной среде с определённой диэлектрической проницаемостью, а следовательно, и применение формулы Борна – Уэбба оказываются более оправданными, чем в методе Борна. Молекулу воды Ван-Аркель и де-Бур представляют себе в виде сферы с радиусом 0,125 нм и электрическим моментом диполя, равным 6,17×10–30 Кл×м (1,85 D).
Метод Ван-Аркеля и де-Бура был развит и уточнён последующими исследователями, особенно К.П.Мищенко с сотрудниками. В своих работах Мищенко учёл асимметрию диполя воды. Такое видоизменение модели молекулы воды позволило учесть различие в гидрофильности анионов и катионов одинаковых размеров и валентностей. При одинаковых размерах катионов и анионов последние гидратируются сильнее. Это явление объясняется асимметрией диполя воды, благодаря которой положительный конец диполя ближе подходит к центру аниона, чем отрицательный конец к центру катиона. Кроме того, Мищенко принял во внимание некоторые дополнительные эффекты, не учтённые предыдущими исследователями, например тепловое движение молекул в гидратной оболочке и дисперсионные силы. Всё это позволило повысить точность и строгость расчётов. 3. Метод Бернала и Фаулера и его модификации. Другое направление теоретических работ по энергиям гидратации начинается с исследований Бернала и Фаулера (1933), посвящённых природе воды и льда. Как известно, вода обладает рядом аномалий. Её плотность увеличивается при плавлении и продолжает расти в интервале температур от 0 до +4°С. При +4°С плотность максимальна и примерно на 10% превышает плотность льда при температуре плавления. Теплоёмкость воды минимальна при +34,5°С.
Эти особенности воды Бернал и Фаулер объяснили угловым строением её молекул и характером распределения в них зарядов (см. рис. 2). Благодаря такому строению молекулы воды оказывают взаимное ориентирующее действие, что приводит к появлению квазикристаллической структуры, изоморфной кремнезёму, то есть имеющей в основе решётку тетраэдра. Кристаллическая структура льда подобна структуре одной из модификаций кремнезёма – тридимита. Предполагается, что при плавлении льда внутри температурного интервала от 0 до +4°С совершается переход от структуры тридимита к другой, более плотной тетраэдрической модификации кремнезема – кварцу. Максимальная плотность воды при +4°С объясняется наложением эффекта уплотнения (связанного с переходом от структуры тридимита к структуре кварца) на эффект температурного расширения. Дальнейшее повышение температуры уменьшает упорядоченность в распределении частиц жидкости и вызывает переход воды в аморфное состояние. При температурах, близких к критической температуре воды, невозможно обнаружить проявления каких-либо элементов квазикристалличности. В настоящее время считается, что структура воды определяется в первую очередь водородными связями между её молекулами. Каждая молекула воды способна образовывать четыре водородные связи – две донорные и две акцепторные, что может приводить к появлению элементов сетки, неустойчивых кластеров или других частично упорядоченных структур. Идеи, высказанные Берналом и Фаулером в их тридимитно-кварцевой теории воды, используются при интерпретации энергетики гидратации ионов. Наиболее последовательно подобный расчёт энергии гидратации отдельных ионов проведён Эли и Эвансом (1938).
|
||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 1365; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.200.93 (0.009 с.) |

 .
. .
. = –
= –  =
=  ,
, =
=  =
=  .
. и А3 = –
и А3 = – 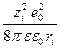 ,
, , выводим основную формулу модели Борна:
, выводим основную формулу модели Борна: .
. = const,
= const, ,
, .
.
 .
.