
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теория электролитов Дебая и ГюккеляСодержание книги
Поиск на нашем сайте Ион-дипольное взаимодействие позволяет физически объяснить образование и устойчивость растворов электролитов. Однако для количественного описания свойств этих растворов необходимо учитывать также ион-ионное взаимодействие. Чтобы описать ион-ионное взаимодействие, необходимо знать распределение ионов в растворе и природу сил, действующих между ионами. Поскольку и ионы, и диполи растворителя находятся в хаотическом движении, а ионы могут образовывать ассоциаты, комплексы и недиссоциированные молекулы, то в общем виде задача о распределении ионов оказывается чрезвычайно сложной. Можно предположить, что электролит полностью диссоциирован (a = 1), растворитель представляет собой непрерывную среду с диэлектрической постоянной e, а ионы взаимодействуют в нем только по закону Кулона. В этих условиях вопрос о распределении и взаимодействии ионов в растворах электролитов был решен Дебаем и Гюккелем (1923). Среди множества ионов, участвующих в хаотическом тепловом движении, в теории Дебая и Гюккеля выбирается один – так называемый центральный ион, который рассматривается как неподвижный. Иначе говоря, начало выбираемой системы координат привязывается к центру этого иона. Вблизи центрального иона некоторым образом распределяются другие ионы. Характер этого распределения обусловлен, во-первых, полем центрального иона, которое убывает с расстоянием r от центрального иона, и, во-вторых, тепловым движением ионов. Поэтому чем ближе к центральному иону, тем больше вероятность того, что там окажется ион противоположного знака. Центральный ион как бы окружен ионной атмосферой. Выбор центрального иона является условным, то есть каждый ион можно рассматривать в качестве центрального и в то же время входящего в состав ионной атмосферы других ионов. Основные положения современной теории растворов электролитов были сформулированы в 1923 г. Дебаем и Гюккелем. Для статистической теории электролитов исходным является следующее положение: ионы распределены в объеме раствора не хаотически, а в соответствии с законом кулоновского взаимодействия. Вокруг каждого отдельного иона существует ионная атмосфера (ионное облако) - сфера, состоящая из ионов противоположного знака. Ионы, входящие в состав сферы, непрерывно обмениваются местами с другими ионами. Все ионы раствора равноценны, каждый из них окружен ионной атмосферой, и в то же время каждый центральный ион входит в состав ионной атмосферы какого-либо другого иона. Существование ионных атмосфер и есть тот характерный признак, который, по Дебаю и Гюккелю, отличает реальные растворы электролитов от идеальных. Энергия, связанная с ионной атмосферой, имеет электрическое происхождение, поэтому она должна быть функцией плотности электрического заряда и потенциала, создаваемого ионной атмосферой. Тепловое движение ионов в ионной атмосфере приводит к тому, что дискретные заряды этих ионов как бы размазываются. В результате ионную атмосферу, состоящую из отдельных ионов, в среднем за некоторый промежуток времени можно моделировать облаком размазанного заряда, плотность которого r уменьшается по мере удаления от центрального иона. Для связи между средней плотностью заряда r и отвечающим ему средним значением потенциала y можно использовать уравнение Пуассона Ñ2y = – где Ñ2 – оператор Лапласа: Ñ2 = Поскольку ионная атмосфера обладает шаровой симметрией, то уравнение Пуассона, записанное в сферической системе координат, принимает вид
и связывает объемную плотность заряда r с потенциалом y на расстоянии r от центрального иона. В уравнение Пуассона входят две неизвестные величины: r и y. Для их определения необходимо иметь второе уравнение, связывающее обе эти переменные. Дебай и Гюккель получили нужное уравнение следующим образом. Для раствора в целом и для любого заданного его объема, достаточно большого по сравнению с размерами иона, справедливо условие электронейтральности å ni ezi = 0, где ni – число ионов i- го сорта в единице объема (если выбран объем раствора, равный единице). Однако заряд некоторого элемента объема dV, находящегося вблизи какого-либо иона, будет отличаться от нуля вследствие существования ионной атмосферы. Если центральный ион, расположенный в начале координат, заряжен положительно, то элемент объема dV будет обладать избыточным отрицательным зарядом. Предполагая, что к распределению ионов в растворе применим принцип Больцмана и что силы, действующие между ионами, по своей природе электростатические, число отрицательных ионов и число положительных ионов в элементарном объеме dV можно выразить как d n – = n – Заряд элемента объема будет равен rdV = ez – n – exp а плотность заряда r = ez – n – exp (учитывая, что в растворе находятся различные ионы, и приписывая zi знак, отвечающий заряду иона). Подстановка r из этого выражения в уравнение Пуассона дает уравнение, которое в общем виде нельзя проинтегрировать. Чтобы упростить его, Дебай и Гюккель предположили, что ezi y << k T, то есть что электростатическое взаимодействие мало по сравнению с термической энергией. Разложив показательную функцию в ряд exp они ограничились только двумя его первыми членами, получив для r следующее уравнение: r = e å zi ni – (так как первый член правой части уравнения по условию электронейтральности равен нулю). Если ввести обозначение c = то после подстановки выражения для r в уравнение Пуассона получаем следующее дифференциальное уравнение:
Общее решение этого уравнения второго порядка имеет вид: y = А1 Константы интегрирования А1 и А2 находят из пограничных условий. Как следует из основных законов электростатики, при r ® ¥ y ® 0; это условие выполняется в том случае, если А2 = 0, так как иначе с удалением от центрального иона y будет стремиться к бесконечности. Для определения А1 в первом приближении теории Дебая – Гюккеля предполагается, что ионы можно отождествить с материальными точками, обладающими определенным зарядом. В этом случае при r ® 0 y должен стремиться к потенциалу самого иона y i, то есть y r ® 0 = y i = что является вторым пограничным условием. Если е –c r разложить в ряд, то получим: y = А1 При r ® 0 всеми членами ряда можно пренебречь по сравнению с 1. Тогда y r ® 0 ® y i = А1/ r, A1 = Величина y в последнем уравнении представляет собой среднее значение потенциала в точке r, создаваемое ионной атмосферой и центральным ионом. Для вычисления ион-ионного взаимодействия представляет интерес не общий потенциал y, а та его часть y а, которая создается ионной атмосферой в месте расположения центрального иона. y а называется потенциалом ионной атмосферы. Его находят по правилу суперпозиции (то есть наложения) потенциалов: y а = y – y i = Для вычисления энергии взаимодействия необходимо определить потенциал ионной атмосферы в точке нахождения центрального иона, то есть найти предел y а при r ® 0. Это можно сделать, используя тот же прием (разлагая показательную функцию в ряд и пренебрегая высшими членами разложения): lim y а = y¢ = – Величину y¢ можно рассматривать как потенциал, создаваемый в точке нахождения центрального иона другим ионом с противоположным знаком, находящимся от центрального иона на расстоянии 1/c. Величина 1/c называется характеристической длиной. Так как потенциал создается не единичным ионом, а всей ионной атмосферой, то 1/c можно отождествить с радиусом ионной атмосферы. Величину c можно рассчитать по вышеприведенному уравнению. В первом приближении теории Дебая и Гюккеля предполагается, что энергия межионного взаимодействия имеет электростатическое происхождение. Энергия взаимодействия между ионами может быть определена поэтому как энергия заряжения центрального иона в электрическом поле ионной атмосферы. Энергия заряжения частицы от 0 до заряда q в поле y равна
(вместо q подставили заряд центрального иона, а вместо y – величину y¢). Найдем выражение для коэффициента активности электролита. Коэффициенты активности первоначально были введены как эмпирические величины; необходимость их введения в уравнения для идеальных систем обусловлена различием между реальными и идеальными растворами. Коэффициенты активности не зависят от метода их определения и при заданных условиях и составе будут иметь одно и то же значение для любых типов равновесия. Таблицы, в которых приведены эмпирические коэффициенты активности, представляют большую ценность. В то же время в пределах теории Льюиса коэффициенты активности оказываются лишь формальными поправочными множителями, не связанными непосредственно с природой растворов и не поддающимися теоретическим расчетам. Реальные растворы отличаются от идеальных энергией взаимодействия между образующими их частицами. Сопоставление выражений для химических потенциалов частиц в реальных растворах m i = m i o + RT ln N i + RT ln g i и в идеальных растворах
показывает, что RT ln g i = m i – Таким образом, коэффициент активности отражает изменение энергетического состояния ионов, обусловленное межионным (межчастичным) взаимодействием. Иначе: коэффициент активности характеризует работу переноса иона из идеального раствора в реальный. Расчет взаимодействия, а следовательно, и коэффициента активности возможен, если известны структура раствора и природа сил взаимодействия между образующими его частицами. Ни то, ни другое не известно с достаточной степенью точности, поэтому для решения проблемы приходится прибегать к некоторым предположениям и создавать модели растворов электролитов. По модели Дебая и Гюккеля, энергия взаимодействия иона с ионной атмосферой, равная энергии заряжения, определяется выражением Dm i = – NA Для коэффициента активности иона получаем ln g i = – NA Подстановка значения c приводит к ln g i = – NA где I – ионная сила раствора, определяемая соотношением I = ( [ ni ] = ион / м 3; [ ni / NA ] = моль / м 3; [ ni /(1000× NA) = ci ] = моль / л). После перехода к десятичному логарифму и подстановки численных значений постоянных величин lg g i = – 1,8246×106 (eT)– 3/2 zi 2 Для данного растворителя и определенной температуры можно написать lg g i = – zi 2 h Для среднего ионного коэффициента активности, который в отличие от коэффициента активности отдельного вида ионов определяется экспериментально, справедливо уравнение lg g± = – ï z+× z –ï h Для водных растворов при 25оС, допуская равенство диэлектрических проницаемостей раствора и растворителя (78,54), h = 0,51. Для 1-1 зарядных электролитов lg g± = – h
|
||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 525; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.23.102.79 (0.007 с.) |

 ,
, +
+ 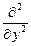 +
+  .
. +
+  = –
= –  dV, d n + = n +
dV, d n + = n +  dV.
dV.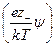 dV – ez + n + exp
dV – ez + n + exp  dV,
dV,
 +
+ 
 å zi2 ni y = –
å zi2 ni y = –  ,
, + А2
+ А2  .
. ,
, (1 – c r +
(1 – c r +  , y =
, y =  =
= 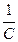
 =
= 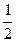
 =
=  c
c = m i o + RT ln N i
= m i o + RT ln N i c.
c.
 .
.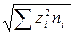 =
=  =
=  =
=  ;
;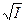 .
.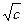 = – 0,51
= – 0,51 


