
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сопоставление теории Дебая – Гюккеля с опытомСодержание книги
Поиск на нашем сайте
Таким образом, теория Дебая и Гюккеля позволяет получить такое же уравнение для коэффициента активности, какое было эмпирически найдено для разбавленных растворов электролитов. Из уравнения (1) следует, что коэффициенты активности в растворах с одинаковой ионной силой должны быть одинаковыми. Это согласуется с законом ионной силы Льюиса – Рендалла, который был открыт раньше, чем была создана теория Дебая и Гюккеля. Теория передает зависимость коэффициентов активности в разбавленных растворах от валентного типа электролита и от температуры. Теория, следовательно, находится в качественном согласии с опытом. Используя выражение для коэффициента активности, можно рассчитать все парциальные термодинамические характеристики раствора (мольную энтропию, мольный объем, теплоемкость, сжимаемость, термическое расширение и т.д.). Теория Дебая и Гюккеля позволила предсказать эффект выделения теплоты при разбавлении растворов электролитов, вызванный тем, что при разбавлении уменьшается взаимодействие между ионами. Учитывая, что вышеприведенные уравнения не содержат эмпирических параметров, успехи теории Дебая – Гюккеля следует признать весьма значительными. При разработке этой теории были сделаны следующие допущения: 1. Число ионов в электролите можно определить из аналитической концентрации электролита, так как он считается полностью диссоциированным (a = 1). Теорию Дебая и Гюккеля поэтому иногда называют теорией полной диссоциации. Однако ее можно применить и в тех случаях, когда a ¹ 1. 2. Распределение ионов вокруг любого центрального иона подчиняется классической статистике Максвелла – Больцмана. 3. Собственными размерами ионов можно пренебречь по сравнению с расстояниями между ними и с общим объемом раствора. Таким образом, ионы отождествляются с материальными точками, и все их свойства сводятся лишь к величине заряда. Это допущение справедливо только для разбавленных растворов. 4. Взаимодействие между ионами исчерпывается кулоновскими силами. Наложение сил теплового движения приводит к такому распределению ионов в растворе, для которого характерна статистическая шаровая ионная атмосфера. Это допущение справедливо лишь для разбавленных растворов. При повышении концентрации среднее расстояние между ионами уменьшается, и наряду с электростатическими силами появляются другие силы, действующие на более близком расстоянии, в первую очередь силы Ван-дер-Ваальса. Возникает необходимость учета взаимодействия не только между данным ионом и его окружением, но и между любыми двумя соседними ионами. 5. При расчетах принимается, что диэлектрические проницаемости раствора и чистого растворителя равны; это справедливо только в случае разбавленных растворов. Таким образом, ряд допущений Дебая и Гюккеля приводит к тому, что их теория может быть применима только к разбавленным растворам электролитов с ионами низкой валентности. Уравнение (1) соответствует этому предельному случаю и выражает так называемый предельный закон Дебая и Гюккеля или первое приближение теории Дебая и Гюккеля. Предельный закон Дебая – Гюккеля дает верные значения коэффициентов активности 1-1 зарядного электролита, особенно в очень разбавленных растворах (с £ 0,01 моль/л). Сходимость теории с опытом ухудшается по мере увеличения концентрации электролита, увеличения зарядов ионов и уменьшения диэлектрической проницаемости растворителя, то есть с ростом сил взаимодействия между ионами. Дальнейшее развитие теории Первая попытка усовершенствовать теорию Дебая и Гюккеля и расширить область ее применения была сделана самими авторами. Во втором приближении они отказались от представления об ионах как о материальных точках (допущение 3) и попытались учесть конечные размеры ионов, наделив каждый электролит некоторым средним диаметром а (при этом изменяется и допущение 4). Приписав ионам определенные размеры, Дебай и Гюккель учли тем самым силы некулоновского происхождения, препятствующие сближению ионов на расстояние, меньшее некоторой величины. Во втором приближении средний коэффициент активности описывается уравнением lg g± = - где h сохраняет прежнее значение; а условно названо средним эффективным диаметром ионов, имеет размерность длины, фактически - эмпирическая постоянная (а по своему физическому смыслу соответствует расстоянию, до которого могут сближаться электрические центры двух ионов, однако сольватация ионов делает эту величину неопределенной, и поэтому значения а подбирают, добиваясь наилучшего соответствия формулы (2) экспериментальным данным); В = c / Сохранив основные положения второго приближения теории, Гюккель учел уменьшение диэлектрической проницаемости с ростом концентрации растворов. Ее уменьшение вызывается ориентацией диполей растворителя вокруг иона, в результате чего снижается их реакция на эффект внешнего поля. Уравнение Гюккеля выглядит следующим образом: lg g± = - где С - эмпирическая константа, лишенная определенного физического смысла. При удачном подборе значений a и С формула Гюккеля хорошо согласуется с опытом и широко используется при расчетах (можно описать экспериментальные данные по g± до с порядка 1-2). При последовательном уменьшении ионной силы уравнение (3) последовательно переходит в формулу второго приближения теории Дебая и Гюккеля (уравнение (2)), а затем в предельный закон Дебая – Гюккеля (уравнение (1)). В процессе развития теории Дебая – Гюккеля и последовательного отказа от принятых допущений улучшается сходимость с опытом и расширяется область ее применимости, однако это достигается ценой превращения теоретических уравнений в полуэмпирические.
Рассмотрим рис. 4. Физической основой падения активности по сравнению с концентрацией является взаимное притяжение частиц. Взаимное отталкивание частиц в растворе должно, наоборот, вызывать увеличение активности. В разбавленных растворах электролитов электростатическое притяжение ионов оказывается преобладающим: g± < 1 и падает с ростом концентрации. Учет собственного размера ионов эквивалентен учету сил отталкивания, не позволяющих ионам сблизиться на расстояние, меньшее а. Второе приближение теории, учитывающее этот фактор, приводит к менее резкому уменьшению коэффициента активности (кривая 2) и позволяет описать опытные данные в более широком интервале концентраций. Однако в концентрированных растворах большая часть молекул воды связана ионами, так что добавление новых порций электролита должно сопровождаться разрушением сольватных оболочек и преодолением сил ион-дипольного взаимодействия. Это эквивалентно преобладанию эффекта взаимного отталкивания ионов над их взаимным притяжением; при этом g± > 1. Таким образом, переход к концентрированным растворам сопровождается резким возрастанием коэффициента активности. Чтобы описать это возрастание, в уравнение третьего приближения теории Дебая и Гюккеля и было формально введено эмпирическое слагаемое C I. Следует отметить, что зависимость коэффициента активности в разбавленных растворах электролитов от температуры оказывается весьма незначительной, поскольку повышение температуры сопровождается уменьшением диэлектрической постоянной растворителя, то есть с ростом Т произведение eТ даже несколько уменьшается. В результате при переходе от 0о к 100оС коэффициент h изменяется от 0,492 до 0,609; в 0,01 М растворе 1-1 валентного электролита это соответствует уменьшению среднего коэффициента активности всего на 2,7% (от 0,893 до 0,869). Следует учитывать, что теория дает средний рациональный коэффициент активности (g±), а экспериментальные данные для растворов обычно приводятся в шкале моляльностей (g±¢) или молярных концентраций (f ±). Средние коэффициенты активности в различных шкалах концентраций связаны следующими соотношениями: f ± = g±¢ где rL и ML – плотность и молекулярная масса чистого растворителя соответственно, M – молекулярная масса растворенного вещества, r – плотность раствора. В разбавленных растворах (с £ 0,01) g±» g±¢, но при больших концентрациях различие в значениях этих величин становится существенным. Во всех концентрационных шкалах средние коэффициенты активности при бесконечном разбавлении стремятся к 1, поскольку при этом ион-ионное взаимодействие стремится к нулю и раствор приобретает идеальные свойства. При описании растворов электролитов за стандартное состояние выбирается гипотетический раствор, в котором активности всех ионов равны единице и одновременно отсутствует ион-ионное взаимодействие (естественно, такое стандартное состояние не может быть реализовано). Существует несколько методов определения активности и коэффициентов активности электролитов. Так, например, активность соли может быть найдена по давлению пара растворителя над раствором, криоскопическим и эбуллиоскопическим методами, по осмотическому давлению. Эти методы для растворов электролитов и неэлектролитов полностью аналогичны. Кроме того, для определения активностей в растворах электролитов может быть использован метод измерения разности потенциалов на концах равновесной электрохимической цепи (метод будет рассмотрен ниже). Во всех методах измеряемые активности в тех или иных координатах экстраполируют на нулевую концентрацию, где g±¢ = 1 или f ± = 1. Активности и коэффициенты активности, полученные различными методами, совпадают в пределах точности эксперимента. Это указывает на то, что термодинамический метод описания взаимодействия в растворах электролитов является правильным и самосогласованным (вспомним, что степени диссоциации, определенные различными методами, оказывались разными). Однако термодинамический метод не раскрывает механизма взаимодействия ионов. Наиболее наглядно это проявляется в том, что при помощи термодинамического метода свойства раствора электролита можно описать как в предположении его полной диссоциации (a = 1), так и при допущении, что электролит диссоциирован лишь частично.
Раздел II. Неравновесные явления в растворах электролитов Лекция 3 Электропроводность растворов электролитов: основные понятия; связь электропроводности со свойствами электролитов и природой растворителя; влияние концентрации и температуры на электропроводность В зависимости от природы токопроводящих частиц все вещества можно условно разделить на пять групп: 1. Непроводящие тела, или изоляторы. В них даже при весьма больших электрических полях не наблюдается прохождения тока. К числу изоляторов относят обычно вещества, для которых удельное сопротивление r больше 106 Ом×м. 2. Проводники первого рода, или электронопроводящие тела. К ним относятся металлы, их некоторые оксиды и углеродистые материалы. Прохождение тока обеспечивается электронами; r лежит в пределах 10–8 – 10–5 Ом×м. Температурный коэффициент проводимости отрицателен, то есть с ростом температуры электропроводность уменьшается. 3. Полупроводники – вещества (некоторые полуметаллы, интерметаллиды, соли, органические соединения), в которых ток переносится электронами и дырками. По электропроводности они располагаются между изоляторами и металлами и их r изменяется в широких пределах (10–7 – 103 Ом×м). Температурный коэффициент электропроводности положителен. 4. Проводники второго рода, или ионные проводники. Ток переносится ионами. К ним относятся многие твердые соли (101 £ r £ 106 Ом×м), ионные расплавы (10–3 < r < 10–1 Ом×м), растворы электролитов (10–2 £ r £ 104 Ом×м). Температурный коэффициент электропроводности положителен. 5. Смешанные проводники – тела, сочетающие электронную и ионную проводимости, например, растворы щелочных и щелочноземельных металлов в жидком аммиаке, некоторые твердые соли. Их электропроводность, а также знак температурного коэффициента проводимости зависят от состава проводника и от температуры (от относительного вклада электронной и ионной составляющих), изменяясь от значений, характерных для чисто ионных проводников, до значений, присущих металлам. Предмет дальнейшего рассмотрения – преимущественно ионные проводники – растворы электролитов.
|
||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 414; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.245.158 (0.011 с.) |

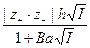 , (2)
, (2) , В незначительно изменяется с Т. Для водных растворов при 25оС произведение В а близко к 1. Формула (2) хорошо описывает поведение многих электролитов вплоть до с = 0,1 (для водных растворов NaCl при 25оС с точностью до 1-2%), однако и во втором приближении нельзя полностью описать весь диапазон зависимости g± от с. Экспериментальные значения g± при высоких концентрациях электролита начинают возрастать, и в некоторых растворах это возрастание очень значительно (в водном растворе HClO4 при m = 16 g± = 500).
, В незначительно изменяется с Т. Для водных растворов при 25оС произведение В а близко к 1. Формула (2) хорошо описывает поведение многих электролитов вплоть до с = 0,1 (для водных растворов NaCl при 25оС с точностью до 1-2%), однако и во втором приближении нельзя полностью описать весь диапазон зависимости g± от с. Экспериментальные значения g± при высоких концентрациях электролита начинают возрастать, и в некоторых растворах это возрастание очень значительно (в водном растворе HClO4 при m = 16 g± = 500).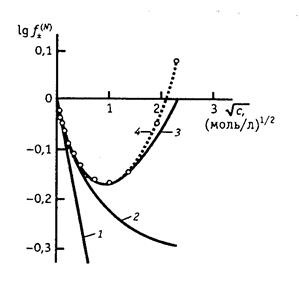
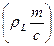 , g± = g±¢ (1 + 0,001nML m), g± = f ± [r – 0,001 с (M – ML)]×(1/rL),
, g± = g±¢ (1 + 0,001nML m), g± = f ± [r – 0,001 с (M – ML)]×(1/rL),


