
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основні правила комбінаторики.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Правило суми. Якщо об’єкт Правило добутку. Якщо деякий об’єкт Правила суми та добутку мають місце для будь-якого скінченого числа множин. Правило суми. Якщо скінченні множини Правило добутку. Нехай треба виконати одну за одною Множина називається впорядкованою, якщо кожному її елементу поставлено у відповідність деяке натуральне число (номер елемента) так, що різним елементам відповідають різні числа. Впорядковані множини вважаються різними, якщо вони відрізняються або своїми елементами, або їх порядком. Перестановкою з
Примітка: Для оцінки Характеристична ознака перестановки: 1) предмети різні; 2) усі місця зайняті; 3) порядок елементів важливий. Розміщенням з
Характеристична ознака розміщень: 1) предмети і місця різні; 2) 3) всі 4) порядок елементів важливий. Комбінацією з
Характеристична ознака комбінацій: 1) предмети різні; 2) 3) порядок вибору елементів не має значення. Властивості комбінацій: 1. 2. 3.
ПРИКЛАДИ РОЗВ’ЯЗАННЯ ТИПОВИХ ЗАДАЧ
Задача 1. Обчислити: а) Розв’язання. а) користуючись формулою (1.2), маємо
в) за властивістю комбінацій та формулою (1.3) дістаємо
Задача 2. Обчислити Розв’язання. Застосовуючи формулу (1.2) отримуємо
Отже,
Задача 3. В інформаційно – технологічному управлінні банку працює три аналітика, десять програмістів та 20 інженерів. Скількома способами начальник управління може вибрати одного співробітника для виконання понад нормованої роботи в святковий день? Розв’язання. Начальник управління може вибрати одного аналітика Задача 4. У шаховому турнірі беруть участь 16 шахістів. Скількома способами можуть бути розподілені перше та друге місця? Розв’язання. Гіпотетично перше місце може вибороти будь-хто з 16 шахістів. Після визначення володаря першого місця друге місце може вибороти будь-хто з 15 інших шахістів. Отже, за правилом добутку, кількість способів розподілу першого та другого місць становить Задача 5. Скільки треба мати словників, щоб можна було робити переклади з будь-якої із шести іноземних мов на будь-яку іншу з них? Розв’язання. Потрібно знайти скількома способами можна вибрати два елементи з даних шести, які відрізняються або порядком або елементами, тому шукане число необхідної кількості буде рівне Задача 6. Скількома способами 4 різні книги можна розставити на полиці? Розв’язання. Кількість таких способів дорівнює числу перестановок з 4 елементів, тобто Задача 7. Скількома способами можна вибрати 4 карти з колоди у 36 карт? Розв’язання. Шукане число дорівнює:
ЗАВДАННЯ ДЛЯ АУДИТОРНОЇ РОБОТИ
1. Обчислити: а) 2. Обчислити 3. Розв’язати рівняння 4. Скільки існує способів вибору на чергування двох студентів з двох груп чисельністю 23 і 20 студентів, якщо студенти з різних груп? 5. Скількома способами можна відібрати одного студента на олімпіаду з математики із двох груп, що складаються з 23 та 20 студентів?
6. Монету підкидають тричі. Скільки різних послідовностей гербів та цифр можна при цьому отримати? 7. На секції математики студентської наукової конференції побажали виступити з доповідями шість студентів. Скількома способами їх можна розмістити в програмі, якщо їх доповіді повинні буди поруч? 8. На п’ять співробітників хімічної лабораторії виділено три оздоровчі путівки. Скількома способами їх можна розділити, якщо: а) всі путівки різні; б) всі путівки однакові? 9. У взводі 3 сержанти і 30 солдатів. Скількома способами можна виділити одного сержанта і трьох солдатів для патрулювання? 10. Скільки чотиризначних чисел можна скласти з цифр 0, 1, 2, 3, 4, 5, якщо: а) жодна з цифр не повторюється; б) цифри можуть повторюватися; в) числа повинні бути непарними (цифри можуть повторюватися)? 11. Скількома способами можна розмістити 10 студентів за круглим столом? 12. У ящику 20 деталей серед яких 4 браковані. Скількома способами можна взяти: а) п’ять деталей; б) одну браковану і чотири стандартні; в) вісім деталей, серед яких 5 стандартних; г) шість деталей серед яких хоча б дві браковані; д) дві однакові за якістю. 13. На книжковій полиці вміщується 10 томів енциклопедії. Скількома способами їх можна розставити так, щоб а)томи 1 і 2 стояли поруч; б) томи 3 і 4 не стояли поруч? Відповіді. 1. а) 324540216; б) 1; в) 120; г) 128. 2.
ДОМАШНЄ ЗАВДАННЯ
1. Обчислити: а) 2. Розв’язати рівняння: а) 3. В магазині «Все до чаю» є п’ять різних чашок та 3 різних блюдця. Скількома способами можна купити чашку з блюдцем? 4. Скільки існує непарних п’ятицифрових чисел? 5. Студенти першого курсу вивчають 8 предметів. Скількома способами можна скласти розклад занять на понеділок, якщо в цей день слід запланувати 3 лекції з різних предметів? 6. На полиці стоїть 8 книжок, з яких 3 книги одного автора. Скількома способами можна переставити книги так, щоб книги одного автора стояли поруч. 7. У букеті 7 червоних і 8 жовтих троянд. З букета навмання виймають 4 троянди. Скількома способами це можна зробити, якщо відомо, що вийняті троянди одного кольору? 8. Скількома способами з колоди (36 карт) можна взяти 4 карти, щоб серед них було: а) три піки; б) дві бубнової, одна чирвової масті; в) всі різної масті. Відповіді. 1. а) 2368371850; б) 363; в) 17100; г) 5760. 2. а)
ОСНОВНІ ТЕОРЕТИЧНІ ВІДОМОСТІ
Теорія ймовірностей – розділ математики, що вивчає математичні моделі випадкових явищ реального світу. Стохастичний або випадковий експеримент – експеримент який можна повторювати необмежену кількість разів і результати якого не можна передбачити наперед. Подія – результат випробування. Достовірною подією називається подія Події, як правило, позначають великими латинськими літерами Простір елементарних подій Елементарною подією називається найпростіший результат випробування і позначається
Операції над подіями. Сумою (об’єднанням) подій
Добутком (перетином) подій
Різницею подій
Протилежною подією
Види випадкових подій. Події Події Події
ПРИКЛАДИ РОЗВ’ЯЗАННЯ ТИПОВИХ ЗАДАЧ
Задача 1. Нехай експеримент полягає в однократному підкиданні грального кубика. Подія Розв’язання. Простором елементарних подій цього експерименту є множина
Сприятливими для настання події Задача 2. Два стрільці по одному разу стріляють по мішені. Подія Розв’язання. Задача 3. Стрілець виконує три постріли по мішені. Нехай подія Розв’язання. Подія Подія Подія Отже,
ЗАВДАННЯ ДЛЯ АУДИТОРНОЇ РОБОТИ
1. Навести приклади достовірних і неможливих подій. 2. Навести приклади сумісних, несумісних, рівноможливих подій. 3. Чи утворюють простір елементарних подій: а) експеримент - підкидання монети, події: 4. Чи є несумісними такі події: а) експеримент ‑ підкидання грального кубика, події:
5. Скільки елементів має простір елементарних подій. а) експеримент ‑ підкидають монету 10 разів; б) експеримент ‑ підкидають гральний кубик шість разів, в) експеримент ‑ два постріли в мішень; г) експеримент ‑ на кожній із чотирьох карток пишуть одну з цифр; 1, 2, 3, 4. 5; д) експеримент- вибір обіду з трьох страв, коли в меню пропонуються 5 перших, 6 других і 3 треті страви; е) експеримент ‑ вибір одного числа із множини всіх п'яти цифрових чисел? 6. Гральний кубик підкидають двічі, описати: а) простір елементарних подій 7. Вийшовши з дому, чоловік зустрів перехожого. Подія 8. 9. Нехай 10. 11. Тричі підкинули монету. Записати простір елементарних подій Відповіді. 3. а) Так; б) Ні; в) Ні; г) Так; д) Ні. 4. а) Ні; б) Так; в) Так; г) Ні; д) Так; е) Так. 5. а) 1024; б) 46656; в) 4; г) 625; д) 90; е) 90000. 11.
ДОМАШНЄ ЗАВДАННЯ
1.
Записати у чому полягають події: 2.
Яка з подій 3. Кидають два гральні кубики. Побудувати простір елементарних подій, а також записати наступні події: 4. У книжковій шафі стоять підручники з математики, теорії ймовірностей, статистики. Студент навмання бере два підручники. Побудувати простір елементарних подій, а також записати наступні події: Відповіді. 4.
|
||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 1280; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.193.71 (0.01 с.) |

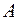 можна вибрати
можна вибрати  способами, а об’єкт
способами, а об’єкт 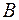 можна вибрати
можна вибрати  способами, то один з об’єктів або
способами, то один з об’єктів або  способами.
способами. способами.
способами. попарно не перетинаються, то число елементів їх об’єднання дорівнює сумі чисел елементів кожної з цих множин.
попарно не перетинаються, то число елементів їх об’єднання дорівнює сумі чисел елементів кожної з цих множин. дій. Якщо першу дію можна виконати
дій. Якщо першу дію можна виконати  способами, другу дію –
способами, другу дію –  способами, третю дію –
способами, третю дію –  способами і так далі до
способами і так далі до  способами, то всі
способами, то всі  способами.
способами. і обчислюють за формулою
і обчислюють за формулою . (1.1)
. (1.1) ,
,  ,
,  .
. при великих
при великих 
 ) називається впорядкована
) називається впорядкована  і обчислюється за формулою
і обчислюється за формулою . (1.2)
. (1.2) ;
; і обчислюється за формулою
і обчислюється за формулою . (1.3)
. (1.3) ,
,  ,
,  ;
; ;
;
 .
. ; б)
; б)  ; в)
; в)  і
і  .
. б) використовуючи формулу (1.1), отримуємо
б) використовуючи формулу (1.1), отримуємо .
. .
. .
. і
і  .
. , звідки
, звідки  , або
, або , тобто
, тобто  .
. способами, одного програміста
способами, одного програміста  способами або одного інженера ‑
способами або одного інженера ‑  способами. Оскільки, за умовою задачі начальник може вибрати будь-кого зі своїх співробітників, то згідно з правилом суми у нього існує
способами. Оскільки, за умовою задачі начальник може вибрати будь-кого зі своїх співробітників, то згідно з правилом суми у нього існує  різних способів вибрати співробітника для виконання понад нормованої роботи.
різних способів вибрати співробітника для виконання понад нормованої роботи.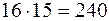 .
. .
. .
. .
. ; б)
; б)  ; в)
; в)  ; г)
; г)  .
. .
. .
. . 3.
. 3.  . 4. 460. 5. 53. 6. 6. 7. 720. 8. а) 60; б) 10. 9. 12180. 10. а) 300; б) 1080; в) 5040. 11. 9!. 12. а) 15504; б) 7280; в) 17472; г) 6000; д) 122.
. 4. 460. 5. 53. 6. 6. 7. 720. 8. а) 60; б) 10. 9. 12180. 10. а) 300; б) 1080; в) 5040. 11. 9!. 12. а) 15504; б) 7280; в) 17472; г) 6000; д) 122. ; б)
; б)  ; в)
; в)  ; г)
; г)  ;
; ; б)
; б) 
 ; б)
; б)  . 3. 15. 4. 45000. 5. 336. 6. 4320. 7. 105. 8. а) 2286; б) 5832; в) 36.
. 3. 15. 4. 45000. 5. 336. 6. 4320. 7. 105. 8. а) 2286; б) 5832; в) 36. , яка при виконанні певного комплексу умов обов’язково відбудеться. Неможлива подія – подія Ø, яка при виконанні даного комплексу умов не може відбутись. Випадкова подія – подія, яка при виконанні даного комплексу умов може як відбутись, так і не відбутись.
, яка при виконанні певного комплексу умов обов’язково відбудеться. Неможлива подія – подія Ø, яка при виконанні даного комплексу умов не може відбутись. Випадкова подія – подія, яка при виконанні даного комплексу умов може як відбутись, так і не відбутись.

 …, або в разі їх значної кількості – великою латинською літерою з індексом
…, або в разі їх значної кількості – великою латинською літерою з індексом  .
. . Простором елементарних подій називається сукупність всіх можливих елементарних подій випробування і позначається
. Простором елементарних подій називається сукупність всіх можливих елементарних подій випробування і позначається  (
( ), яка настає тоді, коли настає принаймні одна з подій
), яка настає тоді, коли настає принаймні одна з подій  є елементарні події, які сприятливі або для події
є елементарні події, які сприятливі або для події 

 (
( ), яка настає тоді, коли настають обидві події
), яка настає тоді, коли настають обидві події  є елементарні події, які сприятливі і для події
є елементарні події, які сприятливі і для події 




 яка настає тоді, коли настає подія
яка настає тоді, коли настає подія 

 до події
до події  .
.
 . В загальному випадку події
. В загальному випадку події  .
. Події
Події  , при
, при 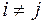 (
( ) і їх множина співпадає з усім простором елементарних подій
) і їх множина співпадає з усім простором елементарних подій  .
.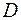 ‑ число очок, більше 6, подія
‑ число очок, більше 6, подія  ‑ число очок, більше 3. Записати простір елементарних подій даного експерименту. Визначити елементарні події, які є сприятливими для вказаних подій. Вказати, які з цих подій: вірогіді, неможливі, рівноможливі.
‑ число очок, більше 3. Записати простір елементарних подій даного експерименту. Визначити елементарні події, які є сприятливими для вказаних подій. Вказати, які з цих подій: вірогіді, неможливі, рівноможливі. , де
, де  ‑ випадання
‑ випадання  очок
очок  . Простір
. Простір 
 ,
,  та
та  , тому
, тому  Сприятливими для події
Сприятливими для події  є такі елементарні події:
є такі елементарні події: 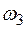 і
і  , тому
, тому  Сприятливими для події
Сприятливими для події  ,
,  ,
,  . Отже, подія
. Отже, подія 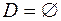 ‑ неможлива подія. Сприятливими для настання події
‑ неможлива подія. Сприятливими для настання події 
 ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  .
. .
.  .
. ,
,  полягає в тому, що стрілець, влучає у мішень при
полягає в тому, що стрілець, влучає у мішень при  .
. ‑ промах при
‑ промах при  .
. Подія
Подія  .
. ‑ випадання непарної цифри,
‑ випадання непарної цифри,  ‑ випадання простого числа; б) експеримент ‑ підкидання симетричної монети, події:
‑ випадання простого числа; б) експеримент ‑ підкидання симетричної монети, події: 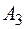 ‑ два влучання; г) експеримент ‑ два постріли в мішень, події:
‑ два влучання; г) експеримент ‑ два постріли в мішень, події:  ‑ випадання парної цифри,
‑ випадання парної цифри,  ; б) подію
; б) подію  ; д) подію
; д) подію  полягає в тому, що він зустрів знайомого, а подія
полягає в тому, що він зустрів знайомого, а подія  ,
,  ,
,  ;
;  ;
;  . Записати у чому полягають події:
. Записати у чому полягають події:  ,
,  ;
;  ;
;  ;
;  ;
;  ;
;  . Яка з подій
. Яка з подій  утворює з подією
утворює з подією  ,
,  ,
,  .
. ;
;  ;
;  .
. ;
; ;
;  .
. ;
; ;
;  ;
; ;
;  .
. ,
,  .
. ;
;  .
.


