
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Ймовірність відхилення відносної частоти від сталої ймовірності в незалежних випробуваннях.Содержание книги
Поиск на нашем сайте
Нехай
ПРИКЛАДИ РОЗВ’ЯЗАННЯ ТИПОВИХ ЗАДАЧ
Задача 1. Ймовірність того, що в один день регіональне представництво Укравтодору в Полтавській області вкладеться в норму витрат на транспорт, дорівнює Розв’язання. Один день робочого тижня можна розглядати як одне незалежне випробування, а весь робочий тиждень ‑ як послідовність
Задача 2. Ймовірність влучення в мішень при одному пострілі дорівнює 0,4. По мішені проводиться шість незалежних пострілів. Знайти ймовірність того, що буде хоча б одне влученя в мішень. Розв’язання. Один постріл по мішені розглядаємо як одне незалежне випробування, а серію з шести пострілів ‑ як послідовність Отже, Задача 3. На АЗС є п’ять заправних колонок. Ймовірність виходу з ладу кожної колонки протягом року дорівнює 0,2. Яка ймовірність того, що протягом року доведеться ремонтувати не більше двох колонок? Розв’язання. Подія Отже,
Задача 4. Автошкола НТУ налічує 9 автомобілів. Відділ технічного контролю перевіряє стан кожного автомобіля, перед його виходом в рейс. Ймовірність того, що в автобіля не пошкоджені склоомивачі 0,85. Знайти наймовірніше число автомобілів, які зможуть вийти в рейс. Розв’язання. За умовою Задача 5. У масовому виробництві автомобільних шин ймовірність браку складає 0,1. Яка ймовірність того, що серед 500 відібраних шин буде 30 бракованих? Розв’язання. За умовою де Тому Задача 6. Ймовірність того, що відвідувач АЗС замовить бензин марки А-95, дорівнює 0,8. Знайти ймовірність того, що із 150 відвідувачів бензин А-95 замовлять не менше 75 і не більше 110 відвідувачів. Розв’язання. За умовою Скористаємося інтегральною теоремою Муавра-Лапласа:
Задача 7. Якщо лівші в середньому складають 2% то яка ймовірність того, що серед 100 чоловік не більше трьох ліворуких? Розв’язання. Скористаємося граничною теоремою Пуассона. За умовою Тоді
Задача 8. Ймовірність того, що деталь, виготовлена заводом, є бракованою, дорівнює 0,02. Для контролю відібрано навмання 1000 деталей. Знайти ймовірність того, що відносна частота бракованих деталей у вибірці відрізняється від ймовірності 0,02, за абсолютною величиною, не більше, ніж на 0,01. Розв’язання. Скористаємося наслідком інтегральної теореми Муавра-Лапласа. За умовою За формулою
отримаємо
Задача 9. Ймовірність браку серед 475 виробів дорівнює 0,05. Знайти з ймовірністю 0,9426 границі, в яких знаходиться число Розв’язання. За умовою
Спочатку знайдемо
За таблицею значень функції Лапласа знаходимо, що
Отже,
ЗАВДАННЯ ДЛЯ АУДИТОРНОЇ РОБОТИ
1. Бізнесмен, вивчивши попит ринку на нові сучасні спортивні автомобілі, вирішив продати пробну партію з дев’яти таких автомобілів. Ймовірність отримати високий прибуток від продажу кожної машини оцінена в 0,8. Яка ймовірність отримати високий прибуток від продажу а) трьох автомобілів; б) не більше трьох автомобілів? 2. Ймовірність того, що витрата бензину автопарком протягом місяця не перевищує встановленої норми, дорівнює 0,95. Знайти ймовірність того, що за півроку роботи автопарк укладеться в норму витрат бензину: а) протягом чотирьох місяців; б) на протязі не меньше чотирьох місяців. 3. На автозавод надійшло 300 ящиків із дзеркалами для автомобілів. Ймовірність того, що у навмання взятому ящику всі дзеркала цілі, дорівнює 0,9. Знайти найімовірніше число ящиків з усіма цілими дзеркалами і обчислити ймовірність такого числа ящиків. 4. Ймовірність того, що в бензині не буде шкідливих домішків в кожній з 5. Чому дорівнює ймовірність 6. Ймовірність того, що кожний відвідувач СТО замовить діагностику двигуна автомобіля, дорівнює 0,64. Знайти ймовірність того, що із 100 відвідувачів замовлять цю діагностику: а) не менше 60 і не більше 70 відвідувачів; б) не менше 60 відвідувачів; в) не більше ніж 75 відвідувачів. 7. Ймовірність того, що пляшка дистильованої води не пройшла контролю якості, дорівнює 0,2. Знайти ймовірність того, що серед 400 випадково відібраних пляшок дистильованої води виявляться неперевіреними від 75 до 100 пляшок. 8. Автозавод відправив 2000 каністр автомобільного мастила. Ймовірність пошкодження кожної каністри в дорозі дорівнює 0,002. Знайти ймовірність того, що під час транспортування буде пошкоджено: а) три каністри автомобільного мастила; б) не більше трьох каністр. 9. Під час випуску інструментів для ремонту автомобілів буває в середньому 4% браку. Визначити ймовірність того, що в партії з 625 інструментів відхилення відносної частоти появи бракованого інструменту від ймовірності його появи за модулем буде не більше ніж 0,02. Відповіді. 1. а) 0,0028; б) 0,0031. 2. а) 0,098; б) 0,983. 3. 0,075. 4. 28, 29. 5.
ДОМАШНЄ ЗАВДАННЯ
1. У масовому виробництві автошин ймовірність браку складає 0,1. Яка ймовірність того, що серед 400 навмання відібраних шин буде 50 бракованих? 2. Ймовірність того, що автомобіль вийде з ладу протягом місяця, дорівнює 0,2. Знайти ймовірність того, що протягом місяця з шести автомобілів вийде з ладу: а) 2 автомобіля; б) хоча б один. 3. Автозавод обслуговує 18 СТО. Від кожної з них заявка на деталі на наступний день може надійти з ймовірністю 0,7. Знайти найімовірніше число заявок на наступний день та ймовірність одержання автозаводом такої кількості заявок. 4. Щоденно 105 автомобілів постачають автомобільні деталі на СТО. Ймовірність безвідмовної роботи кожного з них протягом дня дорівнює 0,8. Знайти ймовірність того, що протягом дня безвідмовно працюватимуть: а) від 70 до 85 автомобілів б) не більше 95 автомобілів. 5. Із оптової бази відправлено на СТО 4000 надійно упакованих доброякісних деталей. Ймовірність того, що одна деталь буде пошкоджена в дорозі, дорівнює 0,0005. Знайти ймовірність того, що на СТО надійде від 3 до 5 пошкоджених деталей. Відповіді. 1. а) 0,016. 2. а) 0,24576; б) 0,738. 3. 0,2. 4. а) 0,59449; б) 0,99632. 5. 0,3067.
ІНДИВІДУАЛЬНІ ЗАВДАННЯ
Завдання 1. В автомобільних перегонах беруть участь три команди з
Завдання 2. В автопарку
Завдання 3. В партії із
Завдання 4. На підприємстві виготовляють автозапчастини: перша лінія виробляє 35% всіх запчастин, друга ‑ 20%, а решту ‑ третя. Брак в їхній продукції складає відповідно
Завдання 5. Ймовірність виходу з ладу за час
Завдання 6. Відділ технічного контролю перевіряє на стандартність
Завдання 7. На підприємство надійшло
Завдання 8. У кожному з
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 2623; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.7.103 (0.007 с.) |

 число настання події
число настання події 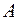 в
в  незалежних випробуваннях, в кожному з яких подія
незалежних випробуваннях, в кожному з яких подія 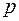
 ,
,  ‑ відносна частота події
‑ відносна частота події  визначається за формулою
визначається за формулою .
. . Яка ймовірність того, що лише в три дні робочого тижня регіональне представництво укладеться в норму витрат?
. Яка ймовірність того, що лише в три дні робочого тижня регіональне представництво укладеться в норму витрат? незалежних випробувань. Подія
незалежних випробувань. Подія  або не настати з ймовірністю
або не настати з ймовірністю 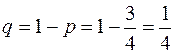 в одному незалежному випробуванні. Ймовірність того, що подія
в одному незалежному випробуванні. Ймовірність того, що подія  рази в
рази в  .
. незалежних випробувань. Подія
незалежних випробувань. Подія  і не відбутись
і не відбутись  в одному незалежному випробуванні. Тоді, для того, щоб знайти ймовірність хоча б одного влучення в ціль використаємо наслідок 8 з формули Бернуллі.
в одному незалежному випробуванні. Тоді, для того, щоб знайти ймовірність хоча б одного влучення в ціль використаємо наслідок 8 з формули Бернуллі. .
. і
і  . Використовуючи наслідок 3 з формули Бернуллі, знайдемо ймовірність того, що серед 5 заправних колонок не більше 2 зламаються протягом року (або жодна, або одна, або дві).
. Використовуючи наслідок 3 з формули Бернуллі, знайдемо ймовірність того, що серед 5 заправних колонок не більше 2 зламаються протягом року (або жодна, або одна, або дві).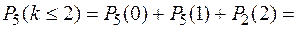
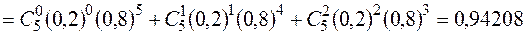 .
. ,
,  ,
,  . Наймовірніше число
. Наймовірніше число  автомобілів в робочому стані задовольняє подвійну нерівність
автомобілів в робочому стані задовольняє подвійну нерівність  або
або 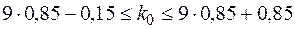 ,
, 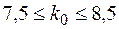 . Отже, найімовірніше в рейс можуть вийти 8 автомобілів.
. Отже, найімовірніше в рейс можуть вийти 8 автомобілів. ,
, 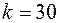 ,
,  ,
,  . Використовуючи локальну теорему Муавра-Лапласа, отримуємо
. Використовуючи локальну теорему Муавра-Лапласа, отримуємо  ,
, , за табл. 1 знаходимо
, за табл. 1 знаходимо  .
.
 .
. ,
,  ,
,  ,
, ,
,  ,
,
 .
. ,
, 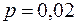 отже,
отже,  .
.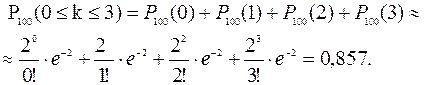
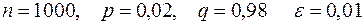 .
.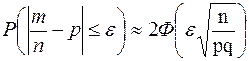 , де
, де  - функція Лапласа,
- функція Лапласа, .
. . Потрібно знайти
. Потрібно знайти  .
.
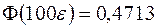 .
. , а значить
, а значить  . Тоді,
. Тоді, ;
; ;
; .
.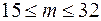
 . 6. а) 0,69108; б) 0,79673; в) 0,98778. 7. 0,99282. 8. а) 0,1954; б) 0,4335. 9. 0,98922.
. 6. а) 0,69108; б) 0,79673; в) 0,98778. 7. 0,99282. 8. а) 0,1954; б) 0,4335. 9. 0,98922. ,
,  та
та 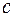 чоловік. Скількома способами можуть розподілитися три призові місця, якщо їх займатимуть члени однієї команди?
чоловік. Скількома способами можуть розподілитися три призові місця, якщо їх займатимуть члени однієї команди?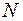 деталей
деталей  стандартних. Навмання відбирається m деталей. Знайти ймовірність того, що серед відібраних m деталей – k стандартних.
стандартних. Навмання відбирається m деталей. Знайти ймовірність того, що серед відібраних m деталей – k стандартних. ,
, 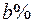 ,
,  .Знайти ймовірність того, що випадково обрана автозапчастина виявиться якісною.
.Знайти ймовірність того, що випадково обрана автозапчастина виявиться якісною. одного конденсатора дорівнює 0,2. Визначити ймовірність того, що за час
одного конденсатора дорівнює 0,2. Визначити ймовірність того, що за час  конденсаторів.
конденсаторів. цієї події відрізняється за модулем від ймовірності
цієї події відрізняється за модулем від ймовірності 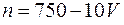 ,
,  ,
,  , де
, де  - номер варіанту.
- номер варіанту.


