
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Формула повної ймовірності. Формула БайєсаСодержание книги
Поиск на нашем сайте
ОСНОВНІ ТЕОРЕТИЧНІ ВІДОМОСТІ
Формула повної ймовірності. Нехай подія Якщо ймовірність гіпотез задано або їх можна обчислити з умов випробування, то ймовірність події
де
При розв’язуванні задач на знаходження повної ймовірності варто дотримуватись такої послідовності: 1) визначити гіпотези і знайти їх ймовірності (якщо гіпотези рівноможливі, то їх ймовірності рівні, а якщо не рівноможливі, їх ймовірності різні, але в обох випадках сума ймовірностей гіпотез дорівнює одиниці); 2) знайти умовні ймовірності; 3) скористатись формулою повної ймовірності. Формула Байєса Подія
Тобто
де Ймовірності подій-гіпотез Зауваження. Гіпотези перевіряються на основі випробувань. Перед початком випробування інколи досить важко визначити апріорні ймовірності цих гіпотез. Кожний дослідник приписує цим гіпотезам певні ймовірності. Метою випробування є розумна корекція цих ймовірностей. Зауваження. Кожне наступне випробування можна починати з апріорними ймовірностями гіпотез, які дорівнюють їх апостеріорним ймовірностям, отриманим у результаті попереднього випробування. Таким чином, на основі випробувань змінюється ступінь довіри до вибраних гіпотез, що зменшує можливість помилки при їх виборі.
ПРИКЛАДИ РОЗВ’ЯЗАННЯ ТИПОВИХ ЗАДАЧ
Задача 1. На трьох автоматичних верстатах виготовляються однакові деталі. Відомо, що 30% продукції виробляється першим верстатом, 25% ‑ другим і 45% ‑ третім. Імовірність виготовлення деталі, що відповідає стандарту, на першому верстаті дорівнює 0,99, на другому ‑ 0,988 і на третьому ‑ 0,98. Виготовлені протягом дня на трьох верстатах невідсортовані деталі знаходяться на складі. Визначити ймовірність того, що взята навмання деталь не відповідає стандарту. Розв’язання. Нехай подія Використовуючи формулу повної ймовірності знаходимо ймовірність того, що вибрана навмання деталь не відповідає стандарту. Отже,
Задача 2. Автомеханічний склад одержує від першого заводу в 4 рази більше агрегатів, ніж від другого. Брак у продукції першого заводу складає 4%, а другого – 8%. а) Знайти ймовірність того, що випадковим чином взятий агрегат виявиться бракованим; б) випадковим способом вибраний агрегат виявився бракованим. Яким заводом він ймовірніше за все виготовлений? Розв’язання.: Нехай подія Ймовірність того, що взятий агрегат бракований за формулою повної ймовірності буде рівною:
Умовні ймовірності гіпотез після того, що в результаті випробування відбулася подія
Отже наймовірніше, що бракована деталь виготовлена першим заводом.
ЗАВДАННЯ ДЛЯ АУДИТОРНОЇ РОБОТИ
1. З урни, яка містить 3 білих та 2 чорних кулі, перекладено дві кулі до урни, яка містить 4 білих і 4 чорних кулі. Яка ймовірність того, що з другої урни після такого перекладання буде взято білу кулю? 2. У трьох урнах лежать білі і сині кулі. У першій – 3 білих і 5 синіх, у другій 6 білих і 4 синіх, в третій – 9 білих і 3 синіх. З навмання взятої урни виймають дві кульки. Знайти ймовірність того, що вони сині. 3. На фабриці виготовляють гвинти. Перша машина виготовляє 25%, друга – 35%, третя – 40% усіх гвинтів. Частка браку відповідно 5%, 4% і 2%. Яка ймовірність того, що випадково вибраний гвинт бракований? 4. Є 30 білетів з яких студент знає 25. У нього є дві можливості: узяти білет першим чи поступившись чергою, другим. Що для нього вигідніше? 5. 60% виробів контролюється першим експертом, 40% другим. Ймовірність забракувати дефектний виріб для першого та другого експерта відповідно 0,9 та 0,7. ймовірність помилкового бракування виробу, що немає дефекту, дорівнює відповідно 0,02 та 0,11. Знайти ймовірності того, що а) дефектний виріб забракують; б) забракують якісний виріб. 6. Дві секретарки заповнюють документи, які складають у спільну папку. Ймовірність того, що помилки в документі зробить перша секретарка становить 0,05, а друга – 0,1. Перша секретарка заповнила 20 документів, а друга – 30. Навмання взятий документ виявився бракованим. Визначити ймовірності того, що його заповнювала перша секретарка. 7. Два стрільці незалежно один від одного роблять по одному пострілу по мішені. Ймовірність влучення першого – 0,7, а другого – 0,35. Відомо, що є одне влучення. Знайти ймовірність того, що в мішень влучив перший стрілець. 8. У контейнер, який містить 3 деталі, про стандартність яких рівноможливі будь-які припущення, додано одну нестандартну деталь. Потім для контролю навмання взято одну деталь. Узята деталь виявилася стандартною. Яким був найбільш ймовірний початковий якісний склад деталей у контейнері? Відповіді. 1. 0,52. 2. 0,19. 3. 0,0345. 4.
ДОМАШНЄ ЗАВДАННЯ
1. В урну, що містить 2 кулі, опущено білу кулю, після чого з неї навмання вилучено одну кулю. Знайти ймовірність того, що вийнята куля виявиться білою, якщо рівноможливі усі можливі припущення про початковий склад куль (за кольором). 2. На складі є 20 нових та 7 використаних інструментів. Першій зміні робітників випадковим чином видається два інструменти, які після роботи повертаються на склад. Друга зміна отримує три інструменти. Яка ймовірність того, що друга зміна одержить три нових інструменти? 3. У першій урні 2 білі і 4 чорні кулі, а у другій - 3 білі і 1 чорна куля. Із першої урни переклали в другу дві кулі. Знайти ймовірність того, що куля, вийнята із другої урни після перекладання, буде білою. 4. На станцію очищення стічних вод 30% стоку надходить з першого підприємства, 40% - з другого, а решта - з третього. Ймовірність появи в стічних водах солей важких металів для першого, другого і третього підприємств відповідно дорівнюють 0,01, 0,02 та 0,04. Визначити ймовірність появи солей важких металів у всьому стоці. 5. Із першої групи, що налічувала 10 студентів, серед яких 4 відмінника, у другу групу, в якій навчалося 8 студентів, серед яких 2 відмінники, було переведено двох студентів. Потім із другої групи для участі в олімпіаді було випадково призначено одного студента. Призначений студент виявився відмінником. Знайдіть імовірність того, що у другу групу було переведено: а) двох відмінників; б) тільки одного відмінника. Відповіді. 1.
|
||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 2114; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.54.100 (0.006 с.) |

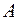 може відбутись лише одночасно з однією з подій
може відбутись лише одночасно з однією з подій  , які утворюють повну групу несумісних подій. Оскільки наперед невідомо, з якою з подій
, які утворюють повну групу несумісних подій. Оскільки наперед невідомо, з якою з подій  відбудеться подія
відбудеться подія  ,
, ‑ ймовірності гіпотез
‑ ймовірності гіпотез  ‑ умовні ймовірності події
‑ умовні ймовірності події  ) та умовні ймовірності того, що подія
) та умовні ймовірності того, що подія  . Відомо, що в результаті випробування подія
. Відомо, що в результаті випробування подія  .
.


 ‑ повна ймовірність події
‑ повна ймовірність події  , називають апріорними. А ймовірності гіпотез
, називають апріорними. А ймовірності гіпотез  називають апостеріорними.
називають апостеріорними. - вибрана деталь виготовлена на першому станку;
- вибрана деталь виготовлена на першому станку;  ‑ вибрана деталь виготовлена на другому верстаті і
‑ вибрана деталь виготовлена на другому верстаті і  ‑ вибрана деталь виготовлена на третьому верстаті. Тоді
‑ вибрана деталь виготовлена на третьому верстаті. Тоді  ,
,  ,
,  і
і  . З умови задачі умовні ймовірності події
. З умови задачі умовні ймовірності події  ‑ ймовірність того, що вибрана нестандартна деталь, була виготовлена першим верстатом,
‑ ймовірність того, що вибрана нестандартна деталь, була виготовлена першим верстатом,  ‑ другим верстатом і
‑ другим верстатом і  ‑ третім верстатом.
‑ третім верстатом.
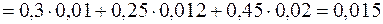 .
. і
і  . Тоді умовні ймовірності відповідно дорівнюють
. Тоді умовні ймовірності відповідно дорівнюють  і
і  .
. .
. ,
, .
. . 5. а) 0,82; б) 0,056. 6. 0,25. 7. 0,8125. 8. 3 стандартні деталі.
. 5. а) 0,82; б) 0,056. 6. 0,25. 7. 0,8125. 8. 3 стандартні деталі. . 2. 0,31. 3.
. 2. 0,31. 3.  . 4. 0,023. 5. а)
. 4. 0,023. 5. а)  ; б)
; б)  .
.


