
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Модуль 1. Елементи теорії ймовірностейСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
МОДУЛЬ 1. ЕЛЕМЕНТИ ТЕОРІЇ ЙМОВІРНОСТЕЙ
ЗМ 1. Елементи комбінаторики. Теорія випадкових подій
Елементи комбінаторики.
ОСНОВНІ ТЕОРЕТИЧНІ ВІДОМОСТІ
Комбінаторика – розділ математики, що вивчає розташування та вибір об’єктів, за певними правилами і методи обчислення всіх можливих, способів якими це можна зробити. Простір елементарних подій Елементарною подією називається найпростіший результат випробування і позначається Операції над подіями. Сумою (об’єднанням) подій
Добутком (перетином) подій
Різницею подій
Протилежною подією
Види випадкових подій. Події Події Події
ПРИКЛАДИ РОЗВ’ЯЗАННЯ ТИПОВИХ ЗАДАЧ
Задача 1. Нехай експеримент полягає в однократному підкиданні грального кубика. Подія Розв’язання. Простором елементарних подій цього експерименту є множина Сприятливими для настання події Задача 2. Два стрільці по одному разу стріляють по мішені. Подія Розв’язання. Задача 3. Стрілець виконує три постріли по мішені. Нехай подія Розв’язання. Подія Подія Подія Отже,
ЗАВДАННЯ ДЛЯ АУДИТОРНОЇ РОБОТИ
1. Навести приклади достовірних і неможливих подій. 2. Навести приклади сумісних, несумісних, рівноможливих подій. 3. Чи утворюють простір елементарних подій: а) експеримент - підкидання монети, події: 4. Чи є несумісними такі події: а) експеримент ‑ підкидання грального кубика, події: 5. Скільки елементів має простір елементарних подій. а) експеримент ‑ підкидають монету 10 разів; б) експеримент ‑ підкидають гральний кубик шість разів, в) експеримент ‑ два постріли в мішень; г) експеримент ‑ на кожній із чотирьох карток пишуть одну з цифр; 1, 2, 3, 4. 5; д) експеримент- вибір обіду з трьох страв, коли в меню пропонуються 5 перших, 6 других і 3 треті страви; е) експеримент ‑ вибір одного числа із множини всіх п'яти цифрових чисел? 6. Гральний кубик підкидають двічі, описати: а) простір елементарних подій 7. Вийшовши з дому, чоловік зустрів перехожого. Подія 8. 9. Нехай 10. 11. Тричі підкинули монету. Записати простір елементарних подій Відповіді. 3. а) Так; б) Ні; в) Ні; г) Так; д) Ні. 4. а) Ні; б) Так; в) Так; г) Ні; д) Так; е) Так. 5. а) 1024; б) 46656; в) 4; г) 625; д) 90; е) 90000. 11.
ДОМАШНЄ ЗАВДАННЯ
1.
Записати у чому полягають події: 2.
Яка з подій 3. Кидають два гральні кубики. Побудувати простір елементарних подій, а також записати наступні події: 4. У книжковій шафі стоять підручники з математики, теорії ймовірностей, статистики. Студент навмання бере два підручники. Побудувати простір елементарних подій, а також записати наступні події: Відповіді. 4.
Властивості ймовірності. 1. Якщо подія 2. Якщо подія 3. Якщо подія
ПРИКЛАДИ РОЗВ’ЯЗАННЯ ТИПОВИХ ЗАДАЧ
Задача 1. Знайти ймовірність того, що при підкиданні грального кубика випала кількість очок кратна трьом. Розв’язання. Нехай подія Задача 2. Академічна група складається з 20 студентів, серед яких є три дівчини. Для походу в театр навмання вибирають 5 студентів. Яка ймовірність того, що серед вибраних студентів будуть 3 хлопці. Розв’язання. Елементарною подією у даному випадку є будь-який вибір 5-ти студентів з двадцяти можливих. Кількість елементарних подій простору Обчислимо кількість елементарних подій, що сприяють події Задача 3. На складі паливно мастильних матеріалів знаходиться 10 каністр з бензином та 5 з дизельним паливом. Яка ймовірність того, що в трьох навмання взятих каністрах виявиться паливо одного виду. Розв’язання. Нехай подія Обчислимо кількість елементарних подій, які сприяють появі події
Тоді, за класичним означенням ймовірності, Задача 4. Вісім автобусів, серед яких два ЛАЗ-697 "Турист", що прибули на станцію технічного обслуговування, випадковим чином розміщені на стоянках, розташованих в одному ряду. Яка ймовірність того, що між автобусами ЛАЗ-697 "Турист" опиниться один автобус іншого типу і не залишиться вільних стоянок, якщо кількість стоянок дорівнює 10? Розв’язання. Нехай подія ‑ між автобусами ЛАЗ-697 "Турист" розташований один автобус іншого типу. Загальна кількість елементарних подій простору Тоді ЗАВДАННЯ ДЛЯ АУДИТОРНОЇ РОБОТИ
1. У ящику 10 куль з номерами від 1 до 10. Дістали одну кулю. Яка ймовірність того, що її номер не перевищує 10? 2. В урні є 20 куль: 12 білих і 8 чорних. Яка ймовірність дістати із урни червону кулю? 3. В урні 15 куль: 5 білих, 6 чорних і 4 синіх. Яка ймовірність дістати: а) білу; б) чорну; в) синю кулю? 4. Монету підкидають двічі. Знайти ймовірність того, що хоча б один раз з’явиться герб. 5. У студентському ансамблі 12 студентів, серед яких 5 хлопців. Яка ймовірність того, що серед 5-и навмання відібраних солістів - 2 хлопці? 6. Студент знає 40 із 100 екзаменаційних питань. Всього екзаменатор задає йому п’ять питань. Знайти ймовірність того, що студент здасть екзамен за умови, що позитивну оцінку ставлять за знання не менш, ніж трьох питань. 7. Знайти ймовірність того, що при підкиданні 3-х гральних кубиків 6 очок випаде на одному з них (байдуже якому), а на гранях двох інших випаде різна кількість очок, причому це не буде 6 очок. 8. На девяти картках написані цифри: 0, 1, 2, 3, 4, 5, 6, 7, 8. Дві з них виймаються навмання, потім читається отримане число, наприклад 07 (сім), 14 (чотирнадцять) і т. д. Знайти ймовірність того, що отримане число буде парним. 9. Слово «форсунка» складається з букв розрізаної азбуки. Навмання, одна за одною, дістали 5 карток і розклали в ряд у порядку появи. Яка ймовірність того, що: а) утвориться слово «фокус»; б) з відібраних карток можна скласти слово «фокус»? 10. Для збирання двигуна автомобіля використовують деталі, які надходять з двох заводів. Перший заводу в середньому дає 1,5% браку, а другий – 1%. Знайти ймовірність потрапляння бракованої деталі, якщо з першого заводу надійшло 2000 деталей, а з другого – 1500. 11. Партія з 34 деталей перевіряється контролером, який навмання відбирає 10 деталей і визначає їх якість. Якщо серед вибраних контролером деталей немає жодної бракованої, то вся партія приймається; в іншому випадку – посилається на додаткову перевірку. Яка ймовірність того, що партія деталей, яка містить 3 браковані деталі, буде прийнята перевіряючим? 12. Сім автомобілів, серед яких два типу Богдан А-092, випадковим чином поставлені в чергу на технічне обслуговування. Знайдіть ймовірність того, що між автомобілями Богдан А-092 опиняться три автомобіля інших типів. 13. У барабані револьвера сім гнізд, в п'ять з них закладені патрони, а два залишені порожніми. Барабан приводиться в обертання, в результаті чого проти стволу випадковим чином виявляється одне з гнізд. Після цього натискається спусковий гачок; якщо комірка була порожня, пострілу не відбувається. Знайти ймовірність того, що, повторивши такий експеримент двічі поспіль, ми обидва рази не вистрілимо. Відповіді. 1. 1. 2. 0. 3. а)
ДОМАШНЄ ЗАВДАННЯ
1. В урні знаходиться 3 червоних, 8 чорних і 9 синіх куль. Яка ймовірність дістати: а) червону; б) чорну; в) синю кулю? 2. Підкидається гральний кубик. Знайти ймовірність: а) появи 3-х очок; б) більше 3-х очок; в) менше 3-х очок; г) парного числа очок; д) непарного числа очок? 3. Регіональне представництво АВТОЗАЗУ отримало з заводу партію з 20 автомобілів, два з них мають істотні дефекти. Одержувач вирішує навмання перевірити три довільні автомобілі з партії та прийняти вантаж, якщо не виявить в жодному з них великі дефекти. Яка ймовірність того, що партію з 20 автомобілів буде прийнято? 4. Маємо 9 однакових за розміром карток, на кожній з яких записано одну з цифр: 1, 2, 3, 4, 5, 6, 7, 8, 9. Навмання беруть 4 картки і розкладають в один рядок. Яка ймовірність того, що при цьому дістанемо число 1972. 5. В урні 10 червоних, 6 синіх і 3 зелених куль однакового розміру. Навмання беруть 6 куль. Яка ймовірність того, що будуть узяті 1 зелена, 2 сині та 3 червоні кулі? 6. Серед 25 студентів групи, в якій є 10 дівчат, розігрують 5 квитків на концерт. Визначити ймовірність того, що білети виграють дві дівчини. 7. В букеті 8 троянд, 6 гвоздик і 3 ромашки. З букету навмання вибирають квіти. З якою ймовірністю можна вибрати: а) одну ромашку; б) дві троянди; в) три квітки одного сорту; г) три квітки різних сортів; д) три троянди й дві ромашки; е) три квітки, серед яких принаймні одна гвоздика. Відповіді. 1. а)
Статистичні ймовірності. Відносною частотою події
Ймовірність Статистичною ймовірністю події
ПРИКЛАДИ РОЗВ’ЯЗАННЯ ТИПОВИХ ЗАДАЧ
Задача 1. Щосуботи два катери прибувають до одного причалу з 9-ї до 10-ї год. ранку. Визначити ймовірність того, що катери зустрінуться, якщо час стоянки біля причалу складає 20 хв. Розв’язання. Розглянемо подію Оскільки простір Визначимо відповідну множину точок площини, які сприяють події
Розв’язання. Нехай подія | |||||||||||||||||||||||||||||||
|
| Поделиться: |

 . Простором елементарних подій називається сукупність всіх можливих елементарних подій випробування і позначається
. Простором елементарних подій називається сукупність всіх можливих елементарних подій випробування і позначається  . Будь-яка підмножина
. Будь-яка підмножина 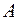 простору елементарних подій називається випадковою подією. Елементарні події, що входять в
простору елементарних подій називається випадковою подією. Елементарні події, що входять в 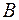 називається подія
називається подія  (
( ), яка настає тоді, коли настає принаймні одна з подій
), яка настає тоді, коли настає принаймні одна з подій  є елементарні події, які сприятливі або для події
є елементарні події, які сприятливі або для події  або для події
або для події 

 (
( ), яка настає тоді, коли настають обидві події
), яка настає тоді, коли настають обидві події  є елементарні події, які сприятливі і для події
є елементарні події, які сприятливі і для події 




 яка настає тоді, коли настає подія
яка настає тоді, коли настає подія 

 до події
до події  .
.
 . В загальному випадку події
. В загальному випадку події  називають попарно несумісними (або просто несумісними), якщо поява однієї з них в даному випробуванні виключає можливість появи будь-якої іншої з цих подій.
називають попарно несумісними (або просто несумісними), якщо поява однієї з них в даному випробуванні виключає можливість появи будь-якої іншої з цих подій. .
. Події
Події  , при
, при 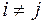 (
( ) і їх множина співпадає з усім простором елементарних подій
) і їх множина співпадає з усім простором елементарних подій  .
. ‑ число очок, не більше 8, подія
‑ число очок, не більше 8, подія 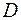 ‑ число очок, більше 6, подія
‑ число очок, більше 6, подія  ‑ число очок, більше 3. Записати простір елементарних подій даного експерименту. Визначити елементарні події, які є сприятливими для вказаних подій. Вказати, які з цих подій: вірогіді, неможливі, рівноможливі.
‑ число очок, більше 3. Записати простір елементарних подій даного експерименту. Визначити елементарні події, які є сприятливими для вказаних подій. Вказати, які з цих подій: вірогіді, неможливі, рівноможливі. , де
, де  ‑ випадання
‑ випадання  очок
очок  . Простір
. Простір 
 ,
,  та
та  , тому
, тому  Сприятливими для події
Сприятливими для події  є такі елементарні події:
є такі елементарні події: 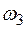 і
і  , тому
, тому  Сприятливими для події
Сприятливими для події  ,
,  ,
,  . Отже, подія
. Отже, подія 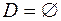 ‑ неможлива подія. Сприятливими для настання події
‑ неможлива подія. Сприятливими для настання події 
 ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  .
. .
.  .
. ,
,  полягає в тому, що стрілець, влучає у мішень при
полягає в тому, що стрілець, влучає у мішень при  .
. ‑ промах при
‑ промах при  .
. Подія
Подія  .
. ‑ випадання непарної цифри,
‑ випадання непарної цифри,  ‑ випадання простого числа; б) експеримент ‑ підкидання симетричної монети, події:
‑ випадання простого числа; б) експеримент ‑ підкидання симетричної монети, події: 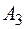 ‑ два влучання; г) експеримент ‑ два постріли в мішень, події:
‑ два влучання; г) експеримент ‑ два постріли в мішень, події:  ‑ випадання парної цифри,
‑ випадання парної цифри,  ; б) подію
; б) подію  ; д) подію
; д) подію  полягає в тому, що він зустрів знайомого, а подія
полягає в тому, що він зустрів знайомого, а подія  ,
,  ,
,  ;
;  ;
;  . Записати у чому полягають події:
. Записати у чому полягають події:  ,
,  ;
;  ;
;  ;
;  ;
;  ;
;  . Яка з подій
. Яка з подій  утворює з подією
утворює з подією  ,
,  ,
,  .
. ;
;  ;
;  .
. ;
; ;
;  .
. ;
; ;
;  ;
; ;
;  .
. ,
,  .
. ;
;  .
. ‑ достовірна, то
‑ достовірна, то 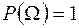 .
. Ø – неможлива, то
Ø – неможлива, то  (Ø)=0.
(Ø)=0. .
. простір елементарних подій. Кількість усіх рівноможливих і єдиноможливих елементарних подій простору
простір елементарних подій. Кількість усіх рівноможливих і єдиноможливих елементарних подій простору  . Подія
. Подія  . Отже, кількість рівноможливих елементарних подій, що сприяють появі події
. Отже, кількість рівноможливих елементарних подій, що сприяють появі події  . Використовуючи класичне означення ймовірності, отримуємо, що
. Використовуючи класичне означення ймовірності, отримуємо, що  .
. дорівнює кількості способів вибору п’яти студентів з двадцяти. Оскільки порядок вибору студентів не має значення, то
дорівнює кількості способів вибору п’яти студентів з двадцяти. Оскільки порядок вибору студентів не має значення, то  .
. способами, а дві дівчини з трьох
способами, а дві дівчини з трьох  . Отже,
. Отже,  . Тоді за класичним означенням ймовірності
. Тоді за класичним означенням ймовірності  .
. .
. способами, а три каністри з дизельним паливом із п’яти можливих
способами, а три каністри з дизельним паливом із п’яти можливих  способами. Отже,
способами. Отже, .
. .
. . Обчислимо скількома способами можна розмістити автобуси, щоб між автобусами ЛАЗ-697 "Турист" розташовувався один автобус іншого типу. Кількість варіантів такого розташування для автобусів ЛАЗ-697 "Турист" з врахуванням варіантів, що виникають при зміні їх місцями, дорівнює 16. Для автобуса, який розташовується між ними, є 6 варіантів, а для решти п’яти автобусів кількість варіантів розташування на семи вільних стоянках дорівнює
. Обчислимо скількома способами можна розмістити автобуси, щоб між автобусами ЛАЗ-697 "Турист" розташовувався один автобус іншого типу. Кількість варіантів такого розташування для автобусів ЛАЗ-697 "Турист" з врахуванням варіантів, що виникають при зміні їх місцями, дорівнює 16. Для автобуса, який розташовується між ними, є 6 варіантів, а для решти п’яти автобусів кількість варіантів розташування на семи вільних стоянках дорівнює  . За принципом добутку число
. За принципом добутку число  наслідків, сприятливих щодо події
наслідків, сприятливих щодо події  .
. .
. ; б)
; б)  ; в)
; в)  . 4.
. 4.  . 5. 0,442. 6. 0,314. 7. 0,278. 8.
. 5. 0,442. 6. 0,314. 7. 0,278. 8. 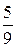 . 9. а) 0,0001; б) 0,018. 10.
. 9. а) 0,0001; б) 0,018. 10.  . 11. 0,338. 12. 0,143. 13. 0,082.
. 11. 0,338. 12. 0,143. 13. 0,082. ; б)
; б) 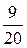 . 2. а)
. 2. а)  ; б)
; б)  ; в)
; в)  ; б) 0,21; в) 0,11; г) 0,21; д) 0,027; е) 0,76.
; б) 0,21; в) 0,11; г) 0,21; д) 0,027; е) 0,76.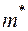 випробувань в яких дана подія
випробувань в яких дана подія  всіх проведених випробувань, тобто
всіх проведених випробувань, тобто .
.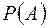 є теоретичною величиною, яка обчислюється до проведення випробування, а відносна частота
є теоретичною величиною, яка обчислюється до проведення випробування, а відносна частота  ‑ величина емпірична, яка обчислюється за результатами проведених випробувань. У дослідах відносна частота коливається навколо деякого сталого числа. Ця властивість відносної частоти називається властивістю стійкості.
‑ величина емпірична, яка обчислюється за результатами проведених випробувань. У дослідах відносна частота коливається навколо деякого сталого числа. Ця властивість відносної частоти називається властивістю стійкості. .
. час прибуття до причалу першого катера, а через
час прибуття до причалу першого катера, а через 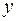 ‑ час прибуття другого катера. Оскільки вони можу прибути протягом години (60 хв.), то
‑ час прибуття другого катера. Оскільки вони можу прибути протягом години (60 хв.), то 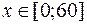 і
і  . Отже, простором елементарних подій
. Отже, простором елементарних подій 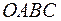 (рис. 4.1).
(рис. 4.1). (різниця між моментами прибуття катерів не перевищує 20 хв.). Це означає, що зустрічі (подія
(різниця між моментами прибуття катерів не перевищує 20 хв.). Це означає, що зустрічі (подія 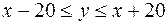 , тобто множина точок сприятливих події
, тобто множина точок сприятливих події 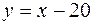 і
і 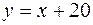 ,утворюючи многокутник
,утворюючи многокутник  . Площа квадрата
. Площа квадрата 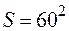 , а площа многокутника
, а площа многокутника 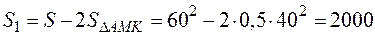 . Тоді шукана ймовірність
. Тоді шукана ймовірність  .
. Задача 2. Всередині еліпса
Задача 2. Всередині еліпса  розміщено коло
розміщено коло 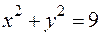 . Знайти ймовірність попадання точки в кільце, обмежене еліпсом і колом (рис. 4.2).
. Знайти ймовірність попадання точки в кільце, обмежене еліпсом і колом (рис. 4.2).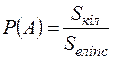 .
. 


