
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Ймовірність випадкової події. Геометричний та статистичний способи обчислення ймовірностей випадкових подій.Содержание книги
Поиск на нашем сайте
ОСНОВНІ ТЕОРЕТИЧНІ ВІДОМОСТІ
Геометричний підхід до обчислення ймовірностей. Класичне обчислення ймовірності застосовують коли числа Ймовірність випадкової події
Зокрема, в одновимірному координатному просторі ймовірність визначається відношенням довжини відрізків; у двовимірному просторі – відношенням площ плоских фігур; у тривимірному просторі – відношенням об’ємів просторових тіл. Статистичні ймовірності. Відносною частотою події
Ймовірність Статистичною ймовірністю події
ПРИКЛАДИ РОЗВ’ЯЗАННЯ ТИПОВИХ ЗАДАЧ
Задача 1. Щосуботи два катери прибувають до одного причалу з 9-ї до 10-ї год. ранку. Визначити ймовірність того, що катери зустрінуться, якщо час стоянки біля причалу складає 20 хв. Розв’язання. Розглянемо подію Оскільки простір Визначимо відповідну множину точок площини, які сприяють події
Розв’язання. Нехай подія Задача 3. По цілі зроблено 24 постріли, з яких було 18 влучень. Яка відносна частота влучень? Розв’язання.
ЗАВДАННЯ ДЛЯ АУДИТОРНОЇ РОБОТИ
1. Хлопчик чекає телефонного дзвінка від друга протягом години. Знайти ймовірність того, що друг зателефонує йому в перші 10 хв. 2. На прямолінійній ділянці газопроводу завдовжки 80 км відбувся розрив. Яка вірогідність того, що розрив віддалений від обох кінців ділянки на відстань, більшу ніж 30 км? 3. Знайти ймовірність того, що сума двох навмання взятих додатних правильних дробів не більше одиниці, а добуток їх не перевищує 4. На нескінченну шахову дошку, сторона кожної клітинки якої дорівнює 5. Відстань між пунктами М і N літак долає за 1 годину, а автомобіль – за 18 годин. Потяг у випадковий час протягом доби вирушає з пункту М до N. Знайти ймовірність того, що черговий літак прибуде до пункту N раніше потяга, якщо між М і N виконується за розкладом один рейс літака щодоби. 6. Два товариші домовились зустрітись в певному місці між 12-ю та 12 год. 40 хв., а також те, що той хто прийде першим, чекатиме іншого впродовж 30 хвилин. Знайти ймовірність того, що зустріч відбудеться, якщо кожний з товаришів, може прийти в будь-який момент часу між 12-ю та 12 год. 40 хв. 7. Два літаки прибувають у зону аеропорту в довільні моменти часу між 17-ю і 18-ю годинами. Посадка літака, що прибув другим, може бути здійснена не раніше ніж через 10 хв. після посадки першого. Знайти ймовірність того, що другому літаку не доведеться чекати посадки. 8. Віконна решітка складається з клітин зі стороною 20см. У грати 100 разів кинули навмання один і той же м'яч. У 50 випадках він пролетів через грати не зачепивши її. Оцініть наближено радіус м'яча. 9. Дослідження показало, що з 1000 потенційних покупців, що зайшли в магазин, дійсно придбало товар 190. Яка відносна частота того, що зайшовши в магазин споживач а) придбає товар б) не придбає товар. 10. Стрілець виробив 100 пострілів по мішені, причому вразив мішень 57 разів. Яка відносна частота того, що стрілець не вразить мішень. 11. Відносна частота появи бракованих виробів на автоматичній строковій лінії складає 0,02. Скільки перевірялося виробів, якщо відомо, що бракованих було 8? Відповіді. 1. ДОМАШНЄ ЗАВДАННЯ
1. Всередині прямокутника, обмеженого осями координат і прямими 2. У круг радіуса 3. Знайти ймовірність того, що навмання вибрана точка правильного трикутника потрапляє в коло, вписане в цей трикутник. 4. Дві особи домовились зустрітись між 14 і 15 годинами. Той, хто прийде першим, чекатиме іншого лише 20 хвилин. Знайти ймовірність того, що зустріч відбудеться, якщо кожна особа може прийти в довільний момент часу між 14 і 15 годинами. 5. Зроблено 20 пострілів по цілі, при цьому виявлено 18 влучень. Знайти відносну частоту влучень. 6. При стрільбі з гвинтівки відносна частота попадання в ціль дорівнює Відповіді. 1.
|
||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 964; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.71.13 (0.008 с.) |

 і
і  скінченні, а результати випробування рівноможливі. Якщо ж множина елементарних подій нескінченна, тобто займає деяку область
скінченні, а результати випробування рівноможливі. Якщо ж множина елементарних подій нескінченна, тобто займає деяку область 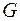 , а події
, а події 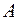 сприяє лише її частина
сприяє лише її частина 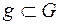 , то користуються геометричним означенням ймовірності.
, то користуються геометричним означенням ймовірності.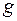 до міри
до міри 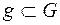 , тобто
, тобто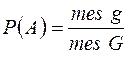 .
.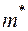 випробувань в яких дана подія
випробувань в яких дана подія  всіх проведених випробувань, тобто
всіх проведених випробувань, тобто .
.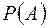 є теоретичною величиною, яка обчислюється до проведення випробування, а відносна частота
є теоретичною величиною, яка обчислюється до проведення випробування, а відносна частота  ‑ величина емпірична, яка обчислюється за результатами проведених випробувань. У дослідах відносна частота коливається навколо деякого сталого числа. Ця властивість відносної частоти називається властивістю стійкості.
‑ величина емпірична, яка обчислюється за результатами проведених випробувань. У дослідах відносна частота коливається навколо деякого сталого числа. Ця властивість відносної частоти називається властивістю стійкості. .
. час прибуття до причалу першого катера, а через
час прибуття до причалу першого катера, а через 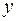 ‑ час прибуття другого катера. Оскільки вони можу прибути протягом години (60 хв.), то
‑ час прибуття другого катера. Оскільки вони можу прибути протягом години (60 хв.), то 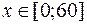 і
і  . Отже, простором елементарних подій
. Отже, простором елементарних подій  даного випадкового експерименту можна вважати точки квадрата
даного випадкового експерименту можна вважати точки квадрата 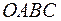 (рис. 4.1).
(рис. 4.1). є неперервним, то ймовірність
є неперервним, то ймовірність  (різниця між моментами прибуття катерів не перевищує 20 хв.). Це означає, що зустрічі (подія
(різниця між моментами прибуття катерів не перевищує 20 хв.). Це означає, що зустрічі (подія 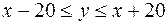 , тобто множина точок сприятливих події
, тобто множина точок сприятливих події 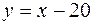 і
і 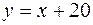 ,утворюючи многокутник
,утворюючи многокутник  . Площа квадрата
. Площа квадрата 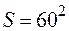 , а площа многокутника
, а площа многокутника 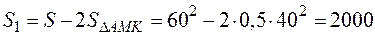 . Тоді шукана ймовірність
. Тоді шукана ймовірність  .
. Задача 2. Всередині еліпса
Задача 2. Всередині еліпса  розміщено коло
розміщено коло 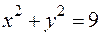 . Знайти ймовірність попадання точки в кільце, обмежене еліпсом і колом (рис. 4.2).
. Знайти ймовірність попадання точки в кільце, обмежене еліпсом і колом (рис. 4.2).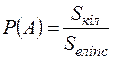 .
. 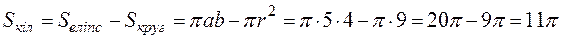 . Таким чином,
. Таким чином, 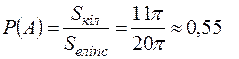 .
.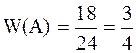 . Таким чином можна зробити висновок, що ймовірність влучень
. Таким чином можна зробити висновок, що ймовірність влучень 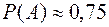 .
.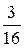 .
.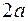 , кидають монету радіуса
, кидають монету радіуса  . Знайти ймовірність того, що монета не перетне сторони клітинки.
. Знайти ймовірність того, що монета не перетне сторони клітинки. . 2.
. 2. 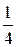 . 3.
. 3. 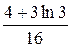 . 4.
. 4. 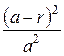 . 5. 0,87. 6. 0,9375. 7. 0,69. 8. 2,93. 9. а) 0,019; б) 0,981. 10. 0,43. 11. 400.
. 5. 0,87. 6. 0,9375. 7. 0,69. 8. 2,93. 9. а) 0,019; б) 0,981. 10. 0,43. 11. 400.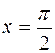 ,
, 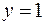 , навмання вибрано точку. Знайти ймовірність того, що вона лежить нижче лінії
, навмання вибрано точку. Знайти ймовірність того, що вона лежить нижче лінії 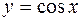 .
.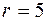 навмання кинуто точку. Знайти ймовірність того, що вона виявиться всередині вписаного в круг квадрата.
навмання кинуто точку. Знайти ймовірність того, що вона виявиться всередині вписаного в круг квадрата.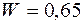 . Знайти число влучень, якщо зроблено 140 пострілів.
. Знайти число влучень, якщо зроблено 140 пострілів.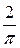 . 2.
. 2. 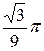 . 4. 0,56. 5. 0,9. 6. 91.
. 4. 0,56. 5. 0,9. 6. 91.


