
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Залежні та незалежні випадкові події. Умовна ймовірність.Содержание книги
Поиск на нашем сайте
Події Ймовірність події Теорема множення ймовірностей незалежних подій. Ймовірність добутку незалежних подій
Декілька подій називають незалежними в сукупності, якщо кожна з них та довільна комбінація інших подій є події незалежні. Наслідок. Нехай подія
Теорема множення ймовірностей залежних подій. Якщо події
Для
ПРИКЛАДИ РОЗВ’ЯЗАННЯ ТИПОВИХ ЗАДАЧ
Задача 1. Під час приймання партії, піддається перевірці половина її виробів. Умовами приймання допускається не більше 2% бракованих виробів. Визначити ймовірність того, що партія з 100 виробів, що містить 5% браку, буде прийнята. Розв’язання. Так як умовою прийняття партії є наявність не більше 2% бракованих виробів з 50 перевірених, тобто не більше одного, то позначимо через З 100 виробів 50 можна вибрати 6 Тоді Задача 2. Відомо, що 3% випущених деталей для телевізора є бракованими, а 80% небракованих деталей ‑ першосортними. Яка ймовірність того, що навмання взята деталь є першосортною? Розв’язання. Нехай подія
Задача 3. Ймовірність влучення в мішень одним стрільцем становить 0,8, іншим ‑ 0,7. Стрільці незалежно один від одного зробили по одному пострілу. Яка ймовірність того, що принаймні один стрілець влучить в мішень? Розв’язання. Нехай подія
Отже, Задача 4. Ймовірність того, що японський автовиробник (лідер світових продажів) має можливість реалізувати свою продукцію через експорт до України 0,7, до Польщі – 0,8, до США – 0,85. Знайти ймовірність того, що підприємство буде експортувати свою продукцію: а) тільки до однієї країни; б) принаймні до двох країн. Розв’язання. Нехай подія Тоді
Подія
Отже,
ЗАВДАННЯ ДЛЯ АУДИТОРНОЇ РОБОТИ
1. Випадковий експеримент полягає в послідовному підкиданні двох монет. Розглядаються події: 2. В ящику 10 червоних і 6 синіх ґудзиків. Навмання виймають два ґудзики. Яка ймовірність того, що ґудзики будуть одного кольору? 3. Знайти ймовірність того, що що навмання вибране двозначне число є кратним 2 або 5, або тому й іншому одночасно. 4. В урні 10 білих і 5 чорних кульок. З урни одну за одною беруть дві кульку. Яка ймовірність того, що другою буде витягнута біла кульку? 5. Три студенти складають залік з «Теорії ймовірностей». Ймовірність успішної здачі для першого дорівнює 0,8, для другого – 0,6, для третього – 0,7. Розглядаються такі події:
6. Прилад складено з двох блоків, з’єднаних паралельно і незалежно працюючих, тобто прилад буде працювати безвідмовно, якщо хоча б один блок не вийде з ладу. Обчислити ймовірність безвідмовної роботи приладу, якщо надійність кожного блоку дорівнює 0,9 і 0,75 відповідно. 7. Три стрільці зробили по одному пострілу по мішені. Ймовірність влучити в мішень для першого стрільця дорівнює 0,8, для другого – 0,75, для третього – 0,9. Знайти ймовірність того, що в мішень влучить перший та хоча б один із решти стрільців. 8. Пошук літака проводиться незалежно двома радіолокаційними станціями. Ймовірність виявлення літака першою станцією дорівнює 0,7. Знайдіть цю ймовірність для другої станції, якщо ймовірність виявлення літака тільки однією станцією дорівнює 0,38. 9. При виготовленні деталі вона послідовно проходить обробку на 4-х верстатах, причому ймовірність, що її зіпсують на кожному з верстатів відповідно дорівнює 0,1, 0,12, 0,2, 0,13. Обчислити ймовірність отримання якісної детелі після повної обробки. 10. Перший оператор обслуговує 43% клієнтів банку, другий – 24%, а третій – 33%. Знайти ймовірність того, що з двох клієнтів які зайшли до банку: а) третій оператор буде обслуговувати одного з них; б) один оператор буде обслуговувати обох клієнтів. 11. Ймовірність принаймні одного влучення стрільцем у мішень при трьох пострілах дорівнює 0,973. Знайти ймовірність влучання при трьох пострілах. Відповіді. 1. а) так; б) ні; в) так; г) так. 2.
ДОМАШНЄ ЗАВДАННЯ
1. Випадковий експеримент полягає в послідовному підкиданні грального кубика двічі. Подія 2. Яка ймовірність того, що при підкиданні грального кубика випаде кількість очок парна, або кратна трьом? 3. На співбесіду прийшло 10 чоловік. Троє з них не кваліфіковані робітики. Представник фірми запросив у кабінет 2-х чоловік. Знайти ймовірність того, що: а) обоє не кваліфіковані; б) другий робітник кваліфікований. 4. Ймовірність безвідмовної роботи блоку, який входить у систему дорівнює 0,7. Для підвищення надійності системи встановлено такий же резерервний блок. Знайти ймовірність зупинки роботи системи з врахуванням такого резервування. 5. Троє гравців грають в дартс. Ймовірність влучення в «яблучко» для першого гравця – 0,6, для другого гравця – 0,8, для третього 0,7. Знайти ймовірність того, що в «яблучко» влучить: 1) принаймні один гравець; 2) три гравці; 3) тільки один з гравців; 4) тільки двоє гравців. 6. Ймовірність того, що студент складе екзамен на відмінно, дорівнює 0,2; на добре - 0,4; на задовільно - 0,3; на незадовільно - 0,1. Визначити ймовірність того, студент складе іспит. 7. Заводом відправлені автомобілі за сировиною на три підприємства. Ймовірність наявності потрібної сировини на першому підприємстві дорівнює 0,6, на другому - 0,95, на третьому - 0,8, на четвертому – 0,75. Знайти ймовірність того, що а) тільки на одному підприємстві не буде потрібної сировини; б) принаймні на одному підприємстві не буде сировини; в) на трьох підприємствах буде потрібна сировини. 8. У команді спортсменів 6 бігунів на короткі дистанції, 3 бігуни на довгі дистанції, 5 стрибунів з жердиною, 7 борців, 4 боксери. Визначити ймовірність того, що навмання викликаний спортсмен виявиться легкоатлетом.
9. Надійшла достатньо велика партія цементу, розфасованого в мішки по 50 кг. Нормальною вважається маса від 49,95 кг до 50,05 кг. Ймовірність того, що маса мішка менша 49,95 кг, дорівнює 0,1; більша 50,05 кг - 0,05. Навмання взято два мішки з цієї партії. Знайти ймовірність того, що: а) обидва мають нормальну масу; б) маса обох мішків не відповідає нормі. 10. Виконано постріл по мішені, яка складається з трьох зон. Ймовірність влучення в першу, другу та третю зони відповідно дорівнюють Відповіді. 1. а) ні. 2. 0,67. 3. а)
|
||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 1954; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.150.72 (0.01 с.) |

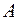 і
і 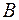 називаються незалежними, якщо ймовірність однієї з них не залежить від того, відбулась чи не відбулась інша подія. В іншому випадку, події
називаються незалежними, якщо ймовірність однієї з них не залежить від того, відбулась чи не відбулась інша подія. В іншому випадку, події  .
. . (5.3)
. (5.3) незалежних у сукупності. Ймовірність події
незалежних у сукупності. Ймовірність події  .
. . (5.4)
. (5.4) залежних подій
залежних подій 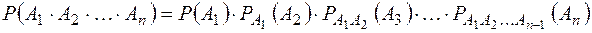 .
. ‑ партія буде прийнята. Партія з 100 виробів, що містить 5% браку (тобто п'ять бракованих виробів), буде прийнята, якщо настане або подія
‑ партія буде прийнята. Партія з 100 виробів, що містить 5% браку (тобто п'ять бракованих виробів), буде прийнята, якщо настане або подія 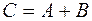 . Так як події
. Так як події  .
.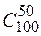 способами. З 95 небракованих виробів 50 можна вибрати
способами. З 95 небракованих виробів 50 можна вибрати  способами. Тоді
способами. Тоді  . Аналогічно
. Аналогічно  .
. .
.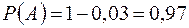 ,
,  (умовна ймовірність). Тоді ймовірність шуканої події
(умовна ймовірність). Тоді ймовірність шуканої події  визначаємо за формулою (5.4):
визначаємо за формулою (5.4):  .
. .
. .
.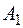 ‑ реалізація продукції на експорт до України; подія
‑ реалізація продукції на експорт до України; подія  ‑ реалізація продукції на експорт до Польщі, подія
‑ реалізація продукції на експорт до Польщі, подія 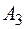 ‑ до США.
‑ до США. 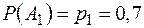 ,
, 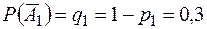 .
.  ,
,  .
.  ,
,  .
. і
і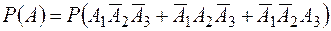 . Так як події
. Так як події  несумісні та незалежні, то
несумісні та незалежні, то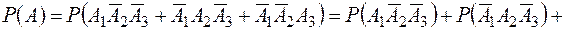
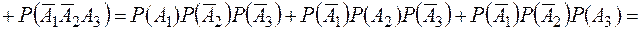

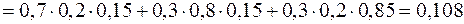 .
. і
і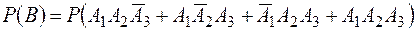 .
.
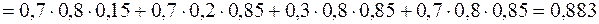 .
.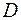 ‑ випадання герба на другій монеті. З'ясувати, чи залежні пари подій: а)
‑ випадання герба на другій монеті. З'ясувати, чи залежні пари подій: а) 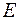 ‑ всі студенти склали залік. Визначне найбільш ймовірну подію.
‑ всі студенти склали залік. Визначне найбільш ймовірну подію. . 3.
. 3.  . 4.
. 4.  . 5.
. 5.  ;
;  ;
;  . Знайти ймовірність промаху.
. Знайти ймовірність промаху. ; б)
; б)  . 4. 0,09. 5. а) 0,976; б) 0,336; в) 0,188; г) 0,452. 6. 0,9. 7. а) 0,4455; б) 0,658; в) 0,4455. 8. 0,56. 9. а) 0,7225; б) 0,0225. 10. 0,45.
. 4. 0,09. 5. а) 0,976; б) 0,336; в) 0,188; г) 0,452. 6. 0,9. 7. а) 0,4455; б) 0,658; в) 0,4455. 8. 0,56. 9. а) 0,7225; б) 0,0225. 10. 0,45.


