
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дерево решений и максимизация полезностиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Как уже отмечалось, согласно гипотезе, предложенной Бернулли и развитой Джоном фон Нейманом и Оскаром Моргенштерном, индивидов интересует ожидаемая полезность рисковых проектов. Функция полезности фон Неймана—Моргенштерна может отражать ранжирование любого количества обусловленных благ. Выражение означает, что индивида фактически интересуют лишь количества обусловленных благ, но оценки этих благ потребителем зависят от вероятностей наступления исходов случайного процесса, ассоциируемых с возможностью их потребления. Вообще говоря, эти вероятности могут входить в функцию полезности достаточно сложным образом, однако имеется, как мы уже знаем, простой и практически важный способ их учета — частный случай, при котором относительное значение, придаваемое индивидом данному обусловленному благу, в точности пропорционально вероятности наступления ассоциируемого с его потреблением исхода. Это — функция ожидаемой полезности. Расчеты ожидаемой полезности каждой из специализаций для Николая Александровича таковы. В области финансового менеджмента:
В области общего менеджмента:
Выбирая вариант, сулящий наибольшую ожидаемую полезность, Николай Александрович решит специализироваться в области финансового менеджмента. Сравнительная статика инвестиционного поведения. Чтобы выявить степень несклонности к риску используют следующие коэффициенты: Коэффициентом абсолютной несклонности к риску Эрроу-Пратта, rA (x) называется rA (x) = Коэффициентом относительной несклонности к риску называется rR(x) = - Будем говорить, что агент с функцией полезности u2(x) обладает б`ольшой несклонностью к риску, чем агент с функцией полезности u1(x), если rA (x) < rR(x), для любого х. Теорема Эрроу-Пратта Пусть предпочтения потребителей 1 и 2 представимы функциями ожидаемой полезности с возрастающими, строго вогнутыми дважды непрерывно дифференцируемыми элементарными функциями полезности. Тогда следующие утверждения эквивалентны: 1) rA1 (x) < rA2 (x) 2) u2(x) = 3) c2(F) < c1(F), для любой лотереи F Будем говорить, что функция u() демонстрирует убывание абсолютной несклонности к риску, если является убывающей функцией х. Изменение степени несклонности к риску. Пусть предпочтения потребителя представимы функцией ожидаемой полезности с возрастающей, строго вогнутой, дважды непрерывно дифференцируемой элементарной функцией полезности. Тогда следующие утверждения эквивалентны: 1) функция u() демонстрирует убывание несклонности к риску; 2) при любом w2<w1u2(z) 3) для любой лотереи F величина w-cw убывает с ростом w, где u(cw(F)) =
Сравнение распределений в терминах риска и доходности Будем считать, что все допустимые распределения удовлетворяют следующим условиям: F(0) = 0 и F(x) = 1 для некоторого х. Будем говорить, что имеет место стохастическое доминирование [3] первой степени распределения F() над распределением G(), если для любой неубывающей функции u выполняется следующее соотношение: Стохастическое доминирование первой степени распределения F() над G() имеет место тогда и только тогда, когда F(x)
Критерий стохастического доминирования второй степени Пусть распределение F() и G() характеризуются одинаковым математическим ожиданием. Стохастическое доминирование второй степени распределения F() над распределением G() имеет место тогда и только тогда, когда
Обобщенная задача инвестора Рассмотрим экономику, где имеется N+1 финансовый актив, один из них (будем называть его нулевым) безрисковый и N рисковых активов. Пусть i-тый актив имеет доходность zi, а F(z1, …, zN) – соответствующая функция распределения. Обозначим через αi долю богатства, инвестируемую в i-тый актив. Предполагая, что агент может занимать по безрисковой ставке, но не может эмитировать рисковые активы, выпишем задачу инвестора:
Теорема Самуэльсона о диверсификации:
[1] Аффинные преобразования, точечные взаимно однозначные отображения плоскости (пространства) на себя, при которых прямые переходят в прямые. Частным случаем аффинных преобразований являются движения и преобразования подобия. [2] (от лат. contingere – случаться) случайность как противоположность необходимости. [3] Критерий стохастического доминирования второго порядка основан на сравнивании не функций распределения доходности портфелей, а интегралов от этих функций, т.е. площадей под функциями распределения. Определим зависимость величины данной площади от значения г как накопленную функцию распределения. Тогда можно сказать, что первый портфель предпочтительнее второго, если накопленная функций распределения его доходности никогда не превосходит, и по крайней мере в одном случае меньше, накопленной функции распределения второго портфеля. Доминирование второго порядка определяется для инвестора не склонного к риску, поэтому оно учитывает тот факт, что ценность единицы богатства для него выше для небольшого уровня богатства и уменьшается с его ростом. В результате инвестор должен в большей степени предпочесть портфель, для которого существует меньшая вероятность принести меньший доход на более нижнем участке распределения доходности, чем на более верхнем. Другими словами, инвестор больше теряет полезности от потери богатства на более нижнем отрезке распределения доходности, чем на более верхнем. В рамках стохастического доминирования второго порядка рассматривается инвестор не склонный к риску, поэтому оно имеет отношение к дисперсии доходности портфелей. Как следует из условия доминирования второго порядка, доминирование первого порядка одного портфеля над другим автоматически предполагает его стохастическое доминирование и второго порядка. Таким образом, условие сто-хастического доминирования второго порядка является более слабым условием. Буренин А.М, «Управление портфелем ценных бумаг»
|
||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 506; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.252.215 (0.007 с.) |

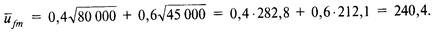
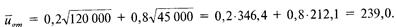
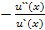 .
. x
x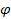 (u1(x)), где
(u1(x)), где  u(w2 + z) является вогнутой трансформацией функции u1(z)
u(w2 + z) является вогнутой трансформацией функции u1(z)  .
.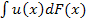

 .
. G(x) для любого x.
G(x) для любого x.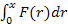

 . для любого х.
. для любого х.


