
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 2 построение функции спроса на основе кардиналистского подхода к оценке полезностиСодержание книги
Поиск на нашем сайте
Кардиналистский(количественный) подход основывается на трех положениях. Первое: потребитель выражает свое желание приобрести какое-либо благо посредством количественной оценки его полезности. Оценки полезности являются субъективными, поскольку важнейшим принципом микроэкономики является принцип субъективизма. Полезность измеряется в ютилах. Существует общая (TU) и предельная (MU) полезности блага Х, где Для моделирования поведения потребителя целесообразно использовать целевую функцию потребления. Такого рода целевая функция является частным случаем функции полезности, которая, в свою очередь, представляет математическую модель потребительских предпочтений. В экономическом анализе в качестве функций полезности часто используются линейные, квадратичные, логарифмические:
функции с постоянной эластичностью замещения:
В прикладных исследованиях спроса и потребления получила распространение линейная модель Стоуна — Джири, целевая функция которой задается в форме:
где hi - коэффициент, задающий приоритет потребления i-го блага; сi - минимальный объем его потребления. В условиях же неопределенности анализ поведения потребителей еще более усложняется. Возникает необходимость выведения функции ожидаемой полезности, что осложняется отсутствием полной или достоверной информации о предлагаемых товарах. Так, функция ожидаемой полезности может быть представлена в следующем виде:
где х – набор благ; p – вероятность получения низкой полезности и степени удовлетворенности; (1-p) – вероятность получения требуемой полезности и степени удовлетворения от набора благ (х). u1 – низкий уровень полезности; u2 – требуемый уровень полезности. Потребитель стремиться максимизировать свою функцию полезности В связи с этим возникает вопрос о выведении косвенной функции полезности. Х. Р. Вэриан отмечает, что косвенная полезность, по определению, является максимальной полезностью при ограничении:
где I — доход индивида; р, — цена на i-е благо; х1,..., хп — купленное индивидом количество благ. Поэтому функция косвенной полезности (indirect utility function) имеет вид:
Второе: в соответствии с первым законом Г.Г. Госсена предельная полезность благ убывает (см. рис. 1.2).
Рис. 1.2 Убывание полезности последующей единицы потребляемого блага
Поскольку предельная полезность – это первая производная функции общей полезности, то если MU = 0, общая полезность – max (min не рассматривается). Третье: по второму закону Г.Г. Госсена оптимум или равновесие потребителя достигается в случае выполнения закона равенства взвешенных предельных полезностей:
Второй закон Госсена иллюстрирует шкала Менгера (см. таблица 1). Таблица 1 Шкала Менгера
Любая диагональ с одинаковыми числами (например 4) показывает оптимальный набор благ, позволяющий получить максимальное удовлетворение от их потребления. Шкала Менгера представляет собой дискретную функцию полезности. Если функция полезности непрерывна, то второй закон Госсена и, соответственно, функция спроса выводятся аналитически. Народно-хозяйственная функция полезности может быть представлена в виде суммы индивидуальных функций полезности по каждому продукту, производимому в народном хозяйстве:
где U - общая сумма полезности; ui (хi) — функции полезности по каждому i-му продукту. Предельная полезность будет первой производной функции полезности: Ui'(хi). Она всегда будет положительной. Общим ограничивающим условием являются совокупные трудовые ресурсы общества:
где N — ресурсы труда, приуроченные к определенному моменту времени; а Т1,..., Тп — количество труда, затрачиваемое на производство каждого вида продукции. Для определения того, какое соотношение должно быть между х1..., хn, если производство ведется целесообразно. Дело сводится к отысканию (по правилам относительных максимумов) функции Лагранжа:
Максимум функции достигается, если удовлетворяется условие вида:
которое иначе можно переписать следующим образом:
При рассмотрении последнего равенства можно обнаружить, что числители дробей в этой формуле есть не что иное, как предельные полезности экономических благ, а знаменатели — трудовые затраты на их производство. Из этой формулы следует, что предельные полезности свободно воспроизводимых экономических благ пропорциональны их трудовым стоимостям.
Контрольные задания
1. Пусть потребитель приобретает три вида блага (А, В,С), функция полезности в этом случае будет иметь следующий вид: U=f (Qa,Qb,Qc). В степенном виде данная функция будет записываться следующим образом:
где α, β и γ– степенные коэффициенты эластичности, 0‹ α ‹1, 0‹ β ‹1 и0‹ γ ‹1. Бюджетное ограничение имеет вид:
С помощью максимизации функции Лагранжа определить структуру покупок, которая обеспечит потребителю получение максимальной полезности. Вывести функции спроса на товары А, Б, С.
При неизменной структур приобретения товаров: (яблоки А, груши В, апельсины С) функция полезности имеет вид:
Доход равен 100 $, Цена яблок (РА) равна 3 $ за 1 кг, Цена груш (РА) равна 5 $ за 1 кг, Цена апельсин (РА) равна 4 $ за 1 кг. Рассчитать структуру покупок.
2. Пусть потребитель приобретает три вида блага (А, В и С), функция полезности будет иметь следующий вид:
где α, β и γ– степенные коэффициенты эластичности, 0‹ α ‹1, 0‹ β ‹1 и0‹ γ ‹1. Бюджетное ограничение имеет вид:
С помощью максимизации функции Лагранжа определить структуру покупок, которая обеспечит потребителю получение максимальной полезности. Вывести функции спроса на товары А, Б, С. 2,3,1, - минимальные объемы потребления каждого блага независимо от их цен. Доход равен 120 $, Цена огурцов (РА) равна 3$ за 1 кг, Цена картошки (РВ) равна 1 $ за 1 кг, Цена мяса (РС) равна 10 $ за 1 кг. Рассчитать структуру покупок.
Тема 3 Теория производства
Теория производства и предложения благ строится на трех основных положениях. Первое положение: общей целью производства является удовлетворение человеческих потребностей. Целью производства как экономической задачи является выбор технологии с наименьшими затратами для получения максимальной прибыли, то есть фирма должна решать и минимизационную, и максимизационную задачи, которые можно объединить в единую задачу рационального ведения хозяйства. Последняя задача предполагает наиболее эффективное соединение всех факторов производства с конкретной целью - максимизации прибыли. В общем виде производственная функция выражается:
где Х1……Хn - факторы производства. Двухфакторная модель будет иметь вид:
Второе: результат производства измеряется тремя показателями. Общий продукт фирмы (TP) это вся продукция фирмы, произведенная с помощью всех задействованных ресурсов. Средний продукт фирмы (AP) характеризует производительность ресурсов.
Предельный продукт (MP) показывает прирост продукции от дополнительной единицы применяемого ресурса:
Третье: выделив отдельно зону рациональной технологии, получим карту изоквант, или линий равного объема, являющихся аналогом кривых безразличия. Вогнутость изоквант объясняется уменьшающейся предельной нормой технического замещения одного ресурса другим:
Характер линии изоквант определяется типом технологии производства. Аналогом бюджетной линии в теории поведения потребителя является изокоста, или равных затрат. В точке оптимума фирмы
Существует три типа отдачи от масштаба производства: убывающая, возрастающая, постоянная.
Типичная зависимость между выпуском продукции и факторами производства в коротком периоде имеет вид:
где α β с- - технологические коэффициенты. В длительном периоде производственная функция примет вид:
где A – коэффициент акселерации; L – труд; K – капитал; a и β – степенные коэффициенты, характеризующие эластичность объема производства по факторам производства. Они показывают, на сколько изменится объем производства при изменении какого-либо фактора на единицу.
где:EQL – коэффициент эластичности объема производства по фактору «труд»;
где EQK – коэффициент эластичности объема производства по фактору «капитал». Если производственная функция имеет вид функции Кобба –Дугласа, то
Если a › β, то это трудоемкая технология, если a ‹ β – капиталоемкая. a + β = 1 - постоянный эффект масштаба; a и β ‹ 1 - возрастающий эффект масштаба; a и β ›1 – убывающий эффект масштаба. Производственная функция Леонтьева имеет вид:
где a и b – технологически необходимые расходы труда и капитала на единицу продукции. Факторы L и K дополняют друг друга (водители и машины). Если факторы не могут заменять друг друга, то MRTS=0. В примере, если на одну машину приходится по два водителя, то при наличии 70 водителей и 40 машин одновременно смогут выйти в рейс 35 машин. Факторы производства могут заменятся, при абсолютной заменяемости факторов MRTS = 1 или в общем случае (const), изокванта при этом будет прямой линией. Кривизна изокванты зависит от степени изменения соотношения предельных производительностей труда и капитала. Количественной мерой этого свойства является эластичность замещения факторов производства (σ). Она показывает, на сколько процентов должна измениться капиталовооруженность труда
Так как В общем виде функция с постоянной эластичностью замещения факторов производства СES (constant elasticity substitution) имеет вид:
В этой формуле эластичность замещения факторов постоянна, хотя и не обязательно равна 1, то есть Производственные функции Кобба-Дугласа и Леонтьева являются частными случаями функции CES. По технологии Кобба-Дугласа заданный объем производства продукции можно произвести при любой капиталовооруженности труда. По технологии Леонтьева, она задается однозначно. Однако, это два крайних варианта, которые не всегда используются на производстве. Чаще всего заданный объем продукции может быть произведен при ограниченном числе различных комбинаций труда и капитала, например, при четырех вариантах выпуска продукции (ABCD). В этом случае изокванта будет ломаной Контрольные задания
1.Заполните пропуски в приведенной таблице, отображающей изменение технической результативности производства при фиксированном объеме капитала и увеличивающемся объеме используемого труда.
2. Фирма работает по технологии, отображаемой производственной функцией 3. Продукция производится по технологии, отображаемой функцией Определить минимум средних затрат в коротком периоде при использовании следующих объемов капитала: К=10,15,20. 4. Вывести функцию предложения из функции затрат в коротком и длительном периодах. Для производства продукции по технологии, соответствующей функции:
где rL; rK – цена капитала и труда. 5. Функция общих затрат фирмы имеет вид TC = 90 Q – 2 Q2 + 0,03 Q 3. Определить величину предельных затрат фирмы при Q = 11 единиц. 6. Известно, что постоянные затраты фирмы 60 ден. ед. Функция предельных затрат фирмы имеет вид МС = 25 –6 Q + 3 Q2 + 2 Q3. Определить функцию общих затрат фирмы и рассчитать эти затраты при выпуске 3 единиц продукции. 7. Функция средних переменных затрат имеет вид AVC = 8 +2 Q. Постоянные затраты равны 15. 8. Найти алгебраическое выражение для функций общих и предельных затрат. Функция общих затрат фирмы имеет вид: TC = 30 + 5 Q + Q2. Определить выражения для постоянных, переменных, предельных, средних общих, средних постоянных, средних переменных затрат как функции от Q. При каком значении Q средние затраты достигают минимума? 9. Постоянные затраты фирмы составляют 60 ден. ед. функция предельных затрат имеет вид: MC = 20 – 10 Q + 6 Q2 + 1,6 Q3. Определить функцию общих затрат фирмы и рассчитать эти затраты при выпуске 5 единиц продукции.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 448; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.220 (0.007 с.) |

 Зависимость между полезностью, получаемой потребителем, и количеством потребляемых им благ называется функцией полезности U = f(x).
Зависимость между полезностью, получаемой потребителем, и количеством потребляемых им благ называется функцией полезности U = f(x). (1.13)
(1.13) (1.14)
(1.14) (1.15)
(1.15)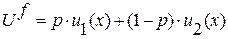 , (1.16)
, (1.16) , (1.17)
, (1.17) (1.18)
(1.18)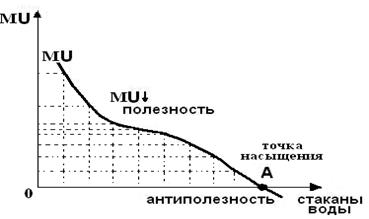
 (1.24)
(1.24) , (1.19)
, (1.19) , (1.20)
, (1.20) (1.21)
(1.21) , (1.22)
, (1.22) (1.23)
(1.23) ,
,
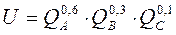
 ,
, ;
; 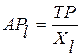 ;
; 
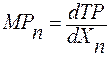


 , при К= const, (2.17)
, при К= const, (2.17)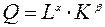 - функция (Кобба-Дугласа), (2.18)
- функция (Кобба-Дугласа), (2.18) , (2.19)
, (2.19) , (2.20)
, (2.20) (2.21)
(2.21)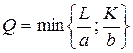 , например,
, например,  (2.22)
(2.22) , чтобы при изменении соотношения производительностей факторов (MRTS) на 1%, выпуск (Q) остался неизменным и находится по формуле:
, чтобы при изменении соотношения производительностей факторов (MRTS) на 1%, выпуск (Q) остался неизменным и находится по формуле: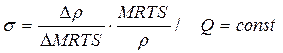 (2.23)
(2.23) , то при технологии, описываемой производственной функцией вида
, то при технологии, описываемой производственной функцией вида  σ =1.
σ =1.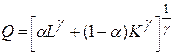 (2.24)
(2.24) ,если γ → 0, то это σ → 1, если γ → ∞, то это σ →0.
,если γ → 0, то это σ → 1, если γ → ∞, то это σ →0. Цена труда – 8 $ цена капитала – 16$. Определить среднюю производительность труда при нахождении фирмы в состоянии равновесия.
Цена труда – 8 $ цена капитала – 16$. Определить среднюю производительность труда при нахождении фирмы в состоянии равновесия. Цены факторов производства равны rL= 1, rL=3.
Цены факторов производства равны rL= 1, rL=3.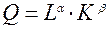 .Зависимость между объемом производства продукции и минимально необходимыми для ее производства затратами называется функцией затрат:
.Зависимость между объемом производства продукции и минимально необходимыми для ее производства затратами называется функцией затрат: ,
,


