
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Механика абсолютно твердого тела. Вращение вокруг неподвижной оси. Момент инерции.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Механика абсолютно твердого тела полностью сводима к механике материальных точек. Абсолютно твёрдое тело — совокупность материальных точек, расстояния между которыми сохраняются в процессе любых движений этого тела (деформация невозможна), обладающая только кинетической энергией поступательного или вращательного движения. Таким образом, положение абсолютно твердого тела полностью определяется, например, положением жестко привязанной к нему декартовой системы координат (обычно ее начало координат делают совпадающим с центром масс твердого тела). При вращении такого тела вокруг неподвижной оси каждая его точка описывает дугу окружности с центром, лежащим на оси, причем все такие окружности лежат в параллельных плоскостях. Так как положение неподвижной оси задано, а расстояние между двумя любыми точками остается неизменным, определить положение тела в пространстве можно с помощью всего одного числа: угол Угловая скорость – это быстрота изменения угла поворота вокруг оси всего тела(!): Если за малый промежуток времени Δ t тело повернется вокруг оси на угол Δ φ, то точка тела, находящаяся на расстоянии R от оси вращения, переместится, пройдя по дуге окружности расстояние Δ s = R Δ φ. Разделив обе части последнего уравнения на Δ t, получим соотношение между величиной линейной скорости V точки и угловой скоростью w вращения: Линейная скорость точек тела при вращении зависит от радиуса окружности: Угловое ускорение – быстрота изменения угловой скорости: Момент инерции – скалярная физическая величина, мера инертности во вращательном движении вокруг оси (как масса в поступательном движении): Теорема Штейнера. Вычисление моментов инерции. Примеры. Теорема Штейнера: момент инерции тела относительно произвольной оси равен сумме момента инерции этого тела относительно параллельной ей оси, проходящей через центр масс тела, и произведения массы тела на квадрат расстояния между осями:
Формулы для вычисления моментов инерции: 1) Кольца, трубки: 2) Сплошного цилиндра, диска: 3) Шара: 4) Стержня:
Колебания. Разные типы колебаний. Колебания — повторяющийся в той или иной степени во времени процесс изменения состояний системы около точки равновесия (попеременное превращение энергии одной формы проявления в другую). Типы колебаний: механические (звук, вибрация), электромагнитные (свет, радиоволны, тепловые), смешанного типа (комбинация). Различают вынужденные, свободные, случайные и т.д. колебания. Гармонические колебания. Основные характеристики колебательного процесса. Дифференциальное уравнение гармонических колебаний. Гармоническими колебаниями называются такие колебания, при которых колеблющаяся величина меняется от времени по закону синуса или косинуса. Уравнение гармонических колебаний имеет вид: где A – амплитуда колебаний (величина наибольшего отклонения системы от положения равновесия);
аргумент косинуса – фаза колебаний. Фаза колебаний определяет смещение колеблющейся величины от положения равновесия в данный момент времени t;
х – смещение. Величина x может принимать значения, лежащие в пределах от -A до +A.
Т – период колебаний – промежуток времени, через который повторяются определенные состояния колебательной системы. Т = 2π называется периодом гармонических колебаний. Период гармонических колебаний равен: T = 2π/ Число колебаний в единицу времени называется частотой колебаний Единица измерения частоты герц (Гц) – одно колебание в секунду. Дважды продифференцировав исходное уравнение по времени, видно, что выполняется следующее соотношение:
|
||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 1106; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.145.168 (0.009 с.) |

 , меняющийся с течением времени, на который повернуто тело вокруг оси относительно некоторого своего положения.
, меняющийся с течением времени, на который повернуто тело вокруг оси относительно некоторого своего положения.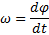


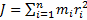
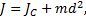 где
где – известныймомент инерции относительно оси, проходящей через центр масс тела,
– известныймомент инерции относительно оси, проходящей через центр масс тела, — искомый момент инерции относительно параллельной оси,
— искомый момент инерции относительно параллельной оси, — масса тела,
— масса тела, — расстояние между указанными осями.
— расстояние между указанными осями. ;
; ;
; ;
; .
.

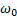 – циклическая частота;
– циклическая частота; :
: 




