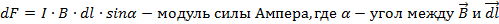Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Проводники в электрическом поле.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Вещество или материальное тело, в котором имеются заряды, способные переносить электрический ток, называется проводником. Незаряженный проводник можно наэлектризовать путем соприкосновения с другим заряженным проводником. При помещении проводника в заряженное поле Е = 0. Вектор напряженности поля на внешней поверхности проводника направлен по нормали к каждой точке его поверхности. Напряженность электростатического поля у поверхности проводника определяется поверхностной плотностью зарядов Поляризация диэлектриков. Поляризуемость. Вектор электрического смещения. Электрическая проницаемость. Поляризация диэлектриков — явление, связанное с ограниченным смещением связанных зарядов в диэлектрике или поворотом электрических диполей, обычно под воздействием внешнего электрического поля, иногда под действием других внешних сил или спонтанно. Поляризуемость — физическое свойство веществ приобретать электрический или магнитный дипольный момент (поляризацию) во внешнем электромагнитном поле. Вектор электрического смещения: Диэлектрическая проницаемость материала:
Электрический ток. Вектор плотности тока. Электрическим током называется любое упорядоченное движение электрических зарядов. В проводнике под действием приложенного электрического поля свободные электрические заряды перемещаются: положительные — по полю, отрицательные — против поля. Количественной мерой электрического тока служит сила тока I, определяемая электрическим зарядом, проходящим через поперечное сечение проводника в единицу времени: Плотность тока — векторная физическая величина, имеющая смысл силы тока, протекающего через единицу площади. В общем случае:
Закон Ома в дифференциальном и интегральном виде. Удельная проводимость и удельное сопротивление. Сопротивление R зависит как от материала, по которому течёт ток, так и от геометрических размеров проводника. Закон Ома в дифференциальной форме, в которой зависимость от геометрических размеров исчезает, и тогда он описывает исключительно электропроводящие свойства материала:
Закон Ома в интегральной форме: падение напряжения на участке цепи равно сумме падений электрического потенциала на этом участке и ЭДС всех источников электрической энергии, включённых на участке: Удельная проводимость – величина, обратно пропорциональная удельному сопротивлению, определяющая способность какого-либо вещества проводить электрический ток. Единица измерения Ом-1м-1. Удельное электрическое сопротивление – способность вещества препятствовать прохождению через него электротока, одним словом, определяющая, насколько легко какой-либо материал пропускает электрический заряд. Единица измерения Ом.м. Действие магнитного поля на проводники с током и движущиеся заряды. Сила действующая на проводник в магнитном поле называется силой Ампера. Сила Ампера, с которой магнитное поле действует на элемент проводника с током, находящегося в магнитном поле, прямо пропорциональна силе тока в проводнике и векторному произведению элемента длины проводника на магнитную индукцию.
Сила действующая на заряд q, движущийся в магнитном поле называется силой Лоренца.
48. - Магнитное поле бесконечного прямого провода и витка с током.
Теорема Гаусса для магнитного поля. Циркуляция магнитного поля.
Магнитное поле в веществе. Различные типы магнетиков.
|
|||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 546; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.19.115 (0.006 с.) |

 . Потенциал поля во всех точках проводника одинаков и равен потенциалу на его поверхности.
. Потенциал поля во всех точках проводника одинаков и равен потенциалу на его поверхности.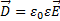 . Необходим для расчёта напряжённости, не меняется при переходе из одной среды в другую.
. Необходим для расчёта напряжённости, не меняется при переходе из одной среды в другую.
 Необходима для применения выше описанных формул.
Необходима для применения выше описанных формул.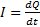 .
.
 – нормальная составляющая вектора плотности тока по отношению к элементу площади dS;
– нормальная составляющая вектора плотности тока по отношению к элементу площади dS;  – специально вводимый вектор элемента площади, ортогональный элементарной площадке и имеющий абсолютную величину, равную её площади, позволяющий записать подынтегральное выражение как обычное скалярное произведение.
– специально вводимый вектор элемента площади, ортогональный элементарной площадке и имеющий абсолютную величину, равную её площади, позволяющий записать подынтегральное выражение как обычное скалярное произведение.
 .
. .
.