
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Материальная точка. Абсолютно твердое тело. Сила; единицы силы.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Содержание технической механики. Роль и значение механики в технике. Теоретическая механика и ее разделы. Техническая механика как наука состоит из 3 разделов: 1.Теоретическая механика 2.Сопротивление материалов 3.Детали машин В свою очередь теоретическая механика состоит из 3 подразделов: 1.Статика (изучает действующие на тела силы) 2.Кинематика (изучает уравнения движения тел) 3.Динамика (изучает движение тел под действием сил) Материальная точка. Абсолютно твердое тело. Сила; единицы силы. Материальная точка – геометрическая точка обладающая массой. Абсолютно твёрдое тело – материальный объект, расстояние между двумя точками на поверхности которого всегда остаётся постоянным. Это цело является ещё и абсолютно жёстким. Любое атт можно рассматривать как систему материальных точек. Мера механического воздействия одного материального объекта на 2-ой – это сила.(н) Сила – векторная величина, которая характеризуется направлением, точкой приложения, числовым значением или модулем силы. Система сил. Эквивалентные системы сил. Равнодействующая сила. Основные задачи статики. Линия вдоль которой осуществляются действие силы называется линия действия силы. Несколько сил действующих на тело образуют систему сил. В статике будем говорить о нескольких системах сил и определять эквиваленты систем. Эквивалентные системы оказывают на тело идентичное действие. Все силы действующие в статике будем делить на внешние и внутренние. Аксиомы статики Аксиома 1. Принцип инерции – всякая изолированная материальная точка находиться в состоянии покоя или равномерного и прямолинейного движения пока приложенные к ней внешние силы не выведут её из этого состояния. Состояние покоя или равномерного прямолинейного движения называют равновесием. Если точка или атт находится под действием системы сил и сохраняют равновесия, то действующая система сил является уравновешенной. Аксиома 2. Условия равновесия двух сил. Две силы приложенные к атт образуют уравновешенную систему если они действуют, вдоль одной прямой и в противоположные стороны и равны по модулю. Аксиома 3. Принцип присоединения и исключения уравновешенных сил. Если на атт действует система сил, то к ней можно добавить или от неё можно отнять уравновешенную систему сил. Полученная новая система будет эквивалентна первоначальной. Следствие 1. Силу приложенную к твёрдому телу можно переносить в любую точку на линии действия, при этом равновесие не нарушается. Аксиома 4. Правила параллелограмма и треугольника. Две приложенные к точке силы имеют равнодействующую приложенную в той же точки равную диагонали параллелограмма построен на этих силах как на сторонах. Такую операцию по замене системы сил равнодействующей силой называют сложением сил. В некоторых случаях правила используются на оборот, т.е. осуществляется преобразование единичной силы систем сходящих сил. Равнодействующее двух сил приложенных к точке тела равна замыкающей стороне треугольника, две другие стороны которого равны первоначальным силам. Следствие 2. Теорема о равновесии трёх сил. Если три действующие на атт параллельные силы образовывают уравновешенную систему, то линии действующих сил пересекаются в одной точке. Аксиома 5. Закон действия и противодействия. При контакте двух тел сила воздействия 1-ого тела на 2-ое равна силе действия 2-ого тела на 1-ое при чём обе силы действуют вдоль прямой и направлены в противоположные стороны. Система сходящихся сил. Сложение плоской системы сходящихся сил. Силовой многоугольник. Систе́ма сходя́щихся сил — это такая система сил, действующих на абсолютно твёрдое тело, в которой линии действия всех сил пересекаются в одной точке. Плоская система сходящихся сил – это такая совокупность действующих на тело сил, линия действия которых пересекается в одной точке. Две силы действующие на тело приложенные к одной точке образуют простейшую систему сходящихся сил. Для операции сложения системы из большего числа сходящихся сил используют правило построения силового многоугольника. При этом последовательно осуществляют операции сложения двух сил. Замыкающая сторона многоугольника и покажет величину направления вектора равнодействующей силы. Аналитическое условие равновесия плоской системы сходящихся сил. В место построения силового многоугольника равнодействующую систему сходящихся сил более точно и быстрее находят вычислением с помощью аналитического способа. В его основе лежит метод проекции с помощью которого координируют каждую систему проецируют на оси координат и вычисляют значение проекции. Если известно направление линии действия силы относительно оси Х то проекция этой силы на ось координат ОХ берётся с функцией косинус а проекция силы на ось У берётся с функцией силы. Если условие задачи направление силы отложено от оси ОУ то расчётную схему необходимо преобразовать высчитав угол между силой и осью ОХ. При определении проекции сил на оси ОХ и ОУ существует правило знаков по которому будем определять направление и соответственно знак проекции. Если относительно проекции оси ох сила совпадает по направлению с положительной составляющей сил, то проекция силы берётся со знаком «+. Если направление силы совпадает с областью отрицательных значений оси то знак проекции -. Это же правило характерно и для оси ОУ. Если сила параллельна одной из осей то проекция силы на эту ось по величине равна самой силы; Проекция этой же силы на другую ось. В ходе решения задач по определению величины равнодействующей силы аналитически это правило используется комплексно, например для заданной системы сходящихся сил построен силовой многоугольник замыкающая сторона которого – равнодействующая система. Спроецируем данный многоугольник на оси координат и определим величину проекций каждой действующей силы. Таким образом проекция равнодействующей системы сходящих сил на каждую из осей координат равна алгебраической суммы проекций составляющих сил на туже ось. Численное значение равнодействующей силы при этом определяется выражением Fe= корень Fex2+Fey2. Задачи по определению неизвестных сил реакций связей, характерные для статики решаются учитывая условия. При этом чаще всего задача решается аналитически а проверка правильности решения графически. В итоге силовой многоугольник должен получиться замкнутым. Геометрическое условие равновесия плоской системы сходящихся сил. . Рассмотрим систему сил действующих над телом и определим величину равнодействующей. В результате последовательного сложения получился вектор суммарной силы который показывает действие системы сил на тело однако построение можно упростить пропуская промежуточные этапы по достроению вектора равнодействующей силы на каждом этапе. Построение силового многоугольника можно вести в любой последовательности. При этом величина и направление вектора равнодействующей силы не изменяются. В статике систему сил действующих на тело считают уравновешенной и если после операции сложения сил получится определённое направление к величины равнодействующая сила – замыкающая сторона многоугольника, то в эту систему необходимо добавить силу численно равную величине суммарного вектора лежащего с ним на одной прямой и противоположно направленную. В ходе построения многоугольника видим что система сил имеет равнодействующую, по этому для соблюдения условий статики добавили силу F5,которое уравновешивает вектор равнодействующих сил. В результате F1 F2 F3 F4 F5 стоит уравновешенной. Таким образом система сходящихся сил расположенных в плоскости уравновешенна тогда, когда силовой многоугольник замкнут. Сложное движение точки. Законы Ньютона сформулированы для движения точки по отношению к инерциальным системам отсчета. Для определения кинематических параметров точки при движении относительно произвольно движущейся системы отсчета вводится теория сложного движения.
Сложным называют движение точки по отношению к двум или нескольким системам отсчета.
Рисунок 3.1 На рисунке 3.1 показаны: - условно принимаемая за неподвижную система отсчета O1x1y1z1; - движущаяся относительно неподвижной система отсчета Oxyz; - точка M, перемещающаяся по отношению к подвижной системе отсчета. Аксиомы динамики. Принцип инерции, Всякое изолированная материальная система находится в состоянии покоя или равномерного и прямолинейного движения пока приложенные внешние силы не выведут её из этого состояния. Это состояние называют инерцией. Меры инертности является масса тела. Масса – количество вещества в единице объёма тела. Второй закон Ньютона – основной закон динамики. F=ma, где F – действующая сила, m- масса тела, а – ускорение точки. Ускорение сообщаемое материальной точке или системе точек силой пропорциональной величине силы и совпадает с направлением силы. На любую точку в пределах земли действует сила тяжести G=mg, где G - сила тяжести определяющая вес тела. Третий закон Ньютона. Силы взаимодействия двух тел равны по величине направлены вдоль одной прямой в противоположные стороны. В динамике при взаимодействии двух тел ускорение обратно пропорционально массе. Закон независимости действия силы. Каждая сила системы оказывает такое же действие на материальный объект как если бы она действовала одна при этом ускорении которое преобразует тело от системы сил равно геометрической сумме ускорений сообщаемых точке каждой силой отдельно. Работа силы тяжести. Рассмотрим перемещение тела по траектории сменяющейся высотой. Работа силы тяжести зависит от изменения высоты и определяется W (b)=G(h1-h2).
При подъёме тела работа силы тяжести отрицательна т.к. под действием силы осуществляется сопротивление движения. При опускании тела работа силы тяжести величина положительная.
Цели и задачи раздела «Детали машин». Механизм и машина. Детали и узлы. Требования, предъявляемые к машинам, узлам и их деталям. Детали машин-наука изучающая метода расчета и конструирования машинных деталей и узлов. В развитии соврем. Машиностроения выделяют выделяют 2 тенденции: 1.непрерывный рост мшиностроения увеличение числа и номенклатуры деталей и узлов общего назначения 2.Повышение мощности и производит.машин их технологичности и,экономичности,веса и размеров оборудования. Машина-устройство выполн. Механ. Движения для преобразования энергии материалов движения с целью повышения производительности и замены труда. Деляться на 2 группы: -машины двигатели(ДВС,поравая машина,электродвигатель) -рабочие машины(оборудование,транспортеры) и другие устройства облегчающие или заменяющие физический труд или логич. Деятельность человека. Механизм-совокупность взаимосвязанных звеньев предназначенные для преобразования движения одного или нескольких элементов машины. Элементарная часть механизма состоящая из нескольких жестко соедин. Деталей-звено.Различают входные и выходные звенья,а также ведущие и ведомые. Все машины и механизмы состоят из деталей и узлов. Деталь изделие изготовленное из одного материала без сборочных операций. Узел-закончен. Сбороч. Единица состоящей из ряда деталей имеющих общее функциональное назначение. Все детали и узлы подразделяются на: 1.Элементы общего назначения А)содинит. Детали и соединения Б)передача вращ. Момента В)детали и узлы обслужив. Передачи Г)опорные детали машин 2.Элементы специального назначения. Основные понятия о надежности и их деталей. Критерии работоспособности и расчета деталей машин. Проектный и проверочный расчет. Надежность обусловлена соблюд. Критериев работоспособности- это свойство отдельной детали или всей машины выполнять заданные функции с сохранением эксплутационных показателей в течении определенного интервала времени. Надежность зависит от особенностей создания и эксплуатации машины.В результате эксплуатации машины при нарушениях возникают неисправности вызывающие потерю. Основным показателем надежности является вероятность безотказной работы Pt-коэффициент надежности,который показывает вероятность того,что в заданном для машины интервале времени(в часах) не возникает отказ.В результате определ. Величина вероятности безотказной работы по формуле Pt=1-Nt/N,где Nt- число машин или деталей отказавших к концу срока службы машины,N- число машин и деталей участвующих в исспытании.Коэффициент надежности всей машины в целом равен коэффициенту Pt=Pt1*Pt2…Ptn.Надежность является одним из основных показателей качества машина,которая связана с работоспособностью. Работоспособность — состояние объекта при котором способен выполнять заданные функции сохраняя значения заданных параметров в пределах установленной техническо-нормативных документаций. Основные критерии работоспособности д.м. является: Прочность, жёсткость, износостойкость, теплостойкость, виброустойчивость. При конструирование д.м. расчёт ведут обычно по одному или двум критериям, остальные критерии удовлетворяются заведомо или не имеют практического значения рассматриваемой детали. Резьбовые соединения. Классификация резьб и основные геометрические резьбы.Основные типы резьб,их сравнительая характеристика и область применения.Конструктивные формы т спобобы стопорения резьбовых соединений. Резьбовым называют соединение составных частей изделия с применением детали, имеющей резьбу. Достоинства резьбовых соединений Недостатки резьбовых соединений Классификация резьб 2) По форме профиля резьбы: 3) По направлению винтовой линии: Принцип работы и устройство фрикционных передач с нерегулируемым (постоянным) передаточным числом. Достоинства и недостатки, область применения. Цилиндрическая передача. Материалы катков. Виды разрушения рабочих поверхностей катков. Фрикционные передачи состоят из двух катков (рис.9.1): ведущего 1 и ведомого 2, которые прижимаются один к другому силой Применение. Фрикционные передачи с нерегулируемым передаточным числом в машиностроении применяются сравнительно редко, например, во фрикционных прессах, молотах, лебедках, буровой технике и т.п.). В качестве силовых передач они громоздки и малонадежны. Эти передачи применяются преимущественно в приборах, где требуется плавность и бесшумность работы (магнитофоны, проигрыватели, спидометры и т. п.). Они уступают зубчатым передачам в несущей способности.
Рис.9.1. Цилиндрическая фрикционная передача: 1 — ведущий каток; 2 — ведомый каток А)Цилиндрическая фрикционная передача применяется для передачи движения между валами с параллельными осями. Б)Коническая фрикционная передача применяется для механизмов у оси валов которых пересекаются. Материалы катков должны обладать: 1.Высшим коэффициентом трения; 2.Высоким параметром износостойкости,прочности,теплопроводности. 3.Высоким модулем упругости,величина которого определяет нагрузочную способность. Сочетания:сталь по стали,чугун по чугуну,композитные материалы по стали. Достоинства фрикционных передач: -плавность и бесшумность работы; -простота конструкций и эксплуатации; -возможность бесступенчатого регулирования передаточного числа; -предохраняют механизмы от поломок при перегрузках вследствия скольжения ведущего катка по ведомому. Недостатки фрикционных передач: -большие нагрузки на валы и подшипники из-за большой силы прижатия катков; -непостоянство передаточного числа из-за за еизбежного упругого скольжения катков; -повышенный износ катков. Фрикционную передачу с параллельными осями валов и с рабочими поверхностями цилиндрической формы называют цилиндрической. Один вал диаметром dx устанавливают на неподвижных подшипниках, подшипники другого вала диаметром d2 — плавающие. Катки 1 и 2 закрепляют на валах с помощью шпонок и прижимают один к другому специальным устройством с силой Fr. Цилиндрические фрикционные передачи с гладкими катками применяют для передачи небольшой мощности (в машиностроении до 10 кВт); эти передачи находят широкое применение в приборостроении. Для одноступенчатых силовых цилиндрических фрикционных передач рекомендуется Общие сведения о цепных передачах: принцип работы, устройство, достоинства и недостатки, область применения. Детали цепных передач (приводные цепи, звездочки). Основные геометрические соотношения в передаче. Передаточное число. Цепные передачи применяются в машинах,где движение между валами передается на значит. Расстоянии(до 8м).исспользуется в машинах,когда зубчатая передача не пригодня,а ременная,не надежна.исспользуется в машинах с максимальной мощности,с окружной скоростью вращения до 15 м/с. Достоинства(по сравнению с ременными): -Более компактны -Значительные большие мощности -Незначительные силы действующие в зацепление,что не вызывает нагружение валов. Недостатки передач: 1.Значительный шум при работе 2.Сравнительно большой износ в цепи 3.Обязательно наличие в конструкции натяжного устройства 4.Относительно высокая стоимость 5.Сложность изготовления цепи Главный элемент передачи привод цепь,состоящая из совокупности шарниров.,соединеных между собой звеньями.Конструкция цепей стандартная и может быть роликовой или зубчато.Цепи могут состоять из одного или нскольких рядов.Должны быть прочными,износостойкими.Звездочки по вешнему виду и конструкции схожи с зубчатыми колёсами.Отличия лишь в профиле зуба,куда при работе передачи попадает цепь.передача наиболее эффективна с максимальным числов зубъев,меньшей звездочки. Передаточное отношение определяется как u=n1/n2=z2/z1.Эта величина состовляет от 1 до 6. Если требуется повысить эту величину,то делают цепную передачу в несколько цепей.КПД=96…98%,а потеря мощности происходит при трении цепи о звездочки и в опорах. Червячная передача с архимедовым червяком. Нарезание червяков и червячных колес. Основные геометрические соотношения. Скорость скольжения в червячной передаче. Передаточное число. Силы, действующие в зацеплении. Виды разрушения зубьев червячных колес. Материалы звеньев червячной пары. Тепловой расчет червячной передачи. Архимедов червяк имеет трапецендальный профиль резьбы в осевом сечении. В торцевом сечении витки резьбы очерчены архимедовой спиралью. Наибольшее применение в машиностроении находят архимедовы червяки, так как технология их производства проста и наиболее отработана. Архимедовы червяки обычно не шлифуют. Их используют когда требуемые твердость материала червяка не превышает 350 НВ. При необходимости шлифовки рабочих поверхностей витков резьбы предпочитают конволютные и эвольвентные червяки, шлифовка которых по сравнению с архимедовым червяком проще и дешевле. Архимедовы червяки подобны ходовым винтам с трапецеидальной резьбой. Основными способами их изготовления являются: 1. Нарезание резцом на токарно-винторезном станке (см. рис 5.4). Этот способ точный, но малопроизводительный. 2. Нарезание модульной фрезой на резьбофрезерном станке. Способ более производительный.
Рис. 5.7. Схема нарезания червячного колеса: Основные геометрические параметры Альфа=200-профильный угол p-шаг зубъев червяка и колеса,соответствующим делительным окружостям червяка и колеса m-осевой модуль z1-число заходов червяков d1=q*m-диаметр делительной окружности da1=d1+2m-диапозон окруж. Выступа dв=d1-2,4m-диаметры окружности впадин время работы червячной передачи витки червяка скользят по зубьям червячного колеса. Рис.5.11 ^ Силы в зацеплении Червячная передача работает с большими тепловыделением.При значительном выделении масла возникает опасность заедания передачи,поэтому составляется уравнение теплового баланса так что бы кол-во выделяемого тепла при максимальной нагрузке передачи. Подшипники скольжения. ПС являются опорами осей и валов,восприним. Нагрузку и равномерно расспределяя её на корпусе узла.От подшипников значительной степени зависит надежности машин.В подшипниках скольжения выделяют 2-е поверхности-по наружной подшипник,жестко устанавливается в корпус,а по внутренней соприкосается с вращ. Валом или осью в результате между подшип. И кнутренним элементом возникает трение скольжения,которое приводит в случаи непрерывной эксплуатации подшипника к нагреву и износу.Для уменьшения поверхности вала и подшипника применяют смазку. Достоинство ПС: -сохраняет работоспособность при очень высоких угловых скоростях вращения -конструкции подшипника смегчает толчки и удары,вибрации,из-за действия масленного слоя. -обеспечив. Установку вала с высокой точностью -возможность создание разъемной конструкции -миним. Радиальные габариты -бесшумность работы Недостатки ПС: -большие потери на преодоление силы трения,особенно при запуске машины -необходимость постоянного ухода за подшипником всдествие высоких требований к смазке. ПС применяется: 1.Высокоскоростные машины. 2.Валы сложной формы 3.При работе в машинах с агрессивными средами и водой 4.Для механизмов раб. С толчками и ударами 5.Для близко расположенных осей и валов с небольшими радиальными зазорами 6.В тихоходных мало ответственных механизмах и машинах. По конструкции корпус подшипника может быть: 1.Неразъемный.Нет вызможности компенсировать износ подшипника.Применяется для опор осей и валов работающих с небольшой нагрузкой. 2.Разъёмные корпус состоит из двух отдельных элементов соединений,которых осущ. Посредством установки подшипника в рабочую машину. Подшипники качения. Подшипники качения представляют собой готовый узел, основным элементом которого являются тела качения – шарики 3 или ролики, установленные между кольцами 1 и 2 и удерживаемые на определенном расстоянии друг от друга обоймой, называемой сепаратором 4. В процессе работы тела качения катятся по дорожкам качения колец, одно из которых в большинстве случаев не-подвижно. Распределение нагрузки между несущими телами качения неравномерно и зависит от величины радиаль-ного зазора в подшипнике и от точности геометрической формы его деталей. В отдельных случаях для уменьшения радиальных размеров подшипника кольца отсутствуют и тела качения катятся непосредственно по цапфе или корпусу. Подшипники качения широко распространены во всех отраслях машиностроения. Они стандартизированы и изго-тавливаются в массовом производстве на ряде крупных специализированных заводов. Достоинства и недостатки подшипников качения Достоинства подшипников качения: По форме тел качения подшипники качения классифицируют на: По направлению воспринимаемой нагрузки подшипники качения классифицируют на: Серии подшипников качения и их обозначение Для каждого типа подшипника при одном и том же внутреннем диаметре имеются различные серии, отличающие-ся размерами колец и тел качения.
Содержание технической механики. Роль и значение механики в технике. Теоретическая механика и ее разделы. Техническая механика как наука состоит из 3 разделов: 1.Теоретическая механика 2.Сопротивление материалов 3.Детали машин В свою очередь теоретическая механика состоит из 3 подразделов: 1.Статика (изучает действующие на тела силы) 2.Кинематика (изучает уравнения движения тел) 3.Динамика (изучает движение тел под действием сил) Материальная точка. Абсолютно твердое тело. Сила; единицы силы. Материальная точка – геометрическая точка обладающая массой. Абсолютно твёрдое тело – материальный объект, расстояние между двумя точками на поверхности которого всегда остаётся постоянным. Это цело является ещё и абсолютно жёстким. Любое атт можно рассматривать как систему материальных точек. Мера механического воздействия одного материального объекта на 2-ой – это сила.(н) Сила – векторная величина, которая характеризуется направлением, точкой приложения, числовым значением или модулем силы.
|
||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 6373; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.248.48 (0.012 с.) |


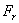 (на рисунке — пружиной), так что сила трения
(на рисунке — пружиной), так что сила трения  в месте контакта катков достаточна для передаваемой окружной силы
в месте контакта катков достаточна для передаваемой окружной силы 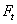 .
.
 .
.





