
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Оценка стоимости денег во времениСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
В процессе управления инвестиционной деятельностью возникает необходимость в проведении специальных расчетов, связанных с движением денежных потоков в различные периоды времени. Ключевую роль в этих расчетах имеет оценка стоимости денег во времени. Концепции, которые оценивают стоимость денег во времени, исходят из предпочтительности денег сегодня, чем завтра, и многие специалисты придерживаются этой линии поведения по двум причинам:
Под влиянием инфляции и других факторов стоимость денег с течением времени изменяется с учетом нормы прибыли, сложившейся на рынке капитала. В качестве последней часто выступает ставка ссудного или депозитного процента, а также норма доходности по государственным ценным бумагам. В данном случае под процентом понимают сумму доходов, полученных от использования денег на финансовом рынке. Учитывают длительность инвестиционного процесса, приходится сравнивать стоимость денег при начале их инвестирования со стоимостью денег при их возврате в форме будущих денежных поступлений (прибыли, амортизационных отчислений, основной суммы долга по кредиту и т. д.).
В процессе сравнения стоимости денег при их инвестировании и возврате принято использовать ряд базовых понятий. Основные из них следующие:
В системе приведенных базовых понятий приоритетным является показатель процентной ставки, применяемый для наращения и дисконтирования денежных потоков. На практике существует многообразие процентных ставок, используемых в финансовых вычислениях. Приведем возможную классификацию процентных ставок.
где Пример. Определить эффективную ставку сложных процентов, если номинальная ставка 16% при ежеквартальном начислении. Тогда
При проведении финансовых операций, связанных с вложением денег в какой-либо вид действия, процессы наращения и дисконтирования можно осуществлять как по простым, там и по сложным процентам. Простые проценты используют, как правило, при краткосрочном инвестировании, а сложные проценты – при долгосрочном.
Простым процентом называют сумму по первоначальной (настоящей) стоимости вклада в конце одного периода платежа, обусловленного условиями инвестирования. Для расчета суммы простого процента в процессе наращения вклада используют следующий алгоритм:
где Пример. Определить сумму простых процентов вклада при следующих условиях:
Тогда будущая стоимость вклада равна: или Для расчета суммы простого процента в процессе дисконтирования денежного потока используют следующий алгоритм:
где Пример. Определить сумму дисконта по проценту за год при следующих условиях: Тогда Настоящая стоимость вклада тогда равна:
Сложным процентом называют величину дохода, который образуется в результате инвестирования при условии, что сумма начисленного процента не выплачивается после каждого периода, а присоединяется к сумме основного вклада, и в последующем расчетном периоде она сама приносит доход (т. е. процент начисляется на процент). Для расчета суммы вклада в процессе наращения (компаундинга) по сложным процентам используют следующий алгоритм:
Пример. Определить будущую стоимость вклада и сумму сложного процента за весь период инвестирования при условии, что первоначальная стоимость вклада PV = 6 млн. руб., процентная ставка для расчета суммы сложного процента – 5% в квартал, общий период инвестирования – 1 год.
Тогда Для расчета настоящей стоимости вклада в процессе дисконтирования денежных потоков используют следующий алгоритм:
Пример. Рассчитать настоящую стоимость вклада и сумму дисконта
Тогда
Существует специальные финансовые таблицы, с помощью которых при заданных размерах процентной ставки и количестве платежных периодов можно определить будущую и настоящую стоимость денег. См. Четыркин Е. М. Финансовая математика. Изд-во «Дело», М., 2009. Ковалев В. В. Финансовый менеджмент. М., 2007.
При оценке стоимости денег во времени необходимо учитывать, что на результаты оценки оказывает большое влияние не только размер процента, но и периодичность выплат (количество платежных периодов в течение одного года). В ряде случаев более выгодно инвестировать денег под меньшую ставку, но с большей периодичностью выплат, например, вклады по депозитам.
Пример. Перед инвестором стоит задача разместить 2,4 млн. руб. в депозитные вклады сроком на 1 год. Первый банк предлагает вкладчику выплачивать доход по сложным процентам 5% 1 раз в квартал, второй банк – 6% 1 раз в 4 месяца, третий банк – 8% 2 раза в году, четвертый банк – 15% 1 раз в год.
Таблица 2.1. Расчет будущей стоимости вклада при различной периодичности начисления сложных процентов и различных процентных ставках
Отдельные виды денежных потоков, оцениваемых во времени, определяют последовательно через равные промежутки времени или в равных размерах. Такую последовательность денежных потоков (равномерных платежей) называют аннуитетом (финансовой рентой). Примером аннуитета могут быть ежеквартальные суммы процентов по облигационным займам, лизинговые платежи за арендуемое имущество и т. д. В практических расчетах на основе специальных алгоритмов устанавливают:
20.09.10
Для определения будущей стоимости аннуитета на основе предварительных (авансовых) платежей применяют следующий алгоритм:
где Пример. Определить будущую стоимость авансового аннуитета, осуществляемого на основе предварительных платежей по следующим данным: сумма каждого отдельного платежа – 3 млн. руб., период платежей – 5 лет, интервал платежей по аннуитету – 1 год; платежи вносятся в начале года; используемая процентная ставка равна 10% годовых. Тогда
Для расчета будущей стоимости аннуитета, осуществляемого на условиях последующих платежей (постнумерандо) применяют формулу:
где Пример. Установить будущую стоимость аннуитета, осуществляемого на условиях последующих платежей по данным предыдущего примера (при условии взноса платежей в конце года). Тогда
Из этих двух примеров следует, что будущая стоимость аннуитета на условиях авансовых платежей обеспечивают инвестору большую сумму дохода.
Для определения настоящей стоимости аннуитета на условиях предварительных платежей используют следующую формулу:
Пример. Установить настоящую стоимость аннуитета при условиях авансовых платежей при следующих данных: период платежа – 5 лет, сумма каждого отдельного платежа – 3 млн. руб., используемая дисконтная ставка – 10% годовых. Тогда
Для расчета настоящей стоимости аннуитета, осуществляемого на условиях последующих платежей (постнумерандо), используют следующий алгоритм:
Пример. Рассчитать настоящую стоимость аннуитета, осуществляемого на условиях последующих платежей (постнумерандо), то есть при условии взноса платежей в конце года, по данным предыдущего примера. Тогда
Из двух выше указанных примеров следует, что настоящая стоимость аннуитета, осуществляемого на условиях авансовых платежей, выше, чем настоящая стоимость аннуитета, осуществляемого на условиях последующих платежей.
Для расчета суммы отдельного платежа при заданной будущей стоимости аннуитета используют следующий алгоритм:
где СОП – сумма отдельного платежа по аннуитету;
Для расчета суммы отдельного платежа при заданной текущей стоимости аннуитета используют следующий алгоритм:
При расчете аннуитета возможно использование упрощенных алгоритмов, основу которых составляет только член аннуитета (сумма отдельного платежа) и соответствующий стандартный множитель (коэффициент) его наращения или дисконтирования.
Упрощенная формула для определения будущей стоимости аннуитета на условиях последующих платежей имеет вид:
где
Упрощенная формула для расчета настоящей стоимости аннуитета на условиях последующих платежей имеет вид:
где
Использование стандартных множителей наращения и дисконтирования стоимости аннуитета значительно упрощает процесс оценки стоимости денег во времени.
|
||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 496; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.38.170 (0.008 с.) |

 ) отражает ее среднегодовой уровень, который определяют отношением годовой суммы процента, начисленного по периодическим ставкам, к основной сумме вклада (капитала). Расчетная формула эффективной ставки процента имеет следующий вид:
) отражает ее среднегодовой уровень, который определяют отношением годовой суммы процента, начисленного по периодическим ставкам, к основной сумме вклада (капитала). Расчетная формула эффективной ставки процента имеет следующий вид: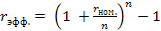 (2.1)
(2.1)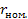 – номинальная процентная ставка,
– номинальная процентная ставка, 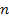 – количество периодов начисления.
– количество периодов начисления.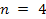 .
.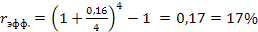 . Следует помнить, что эффективная ставка всегда больше номинальной ставки (которую также называют объявленной процентной ставкой):
. Следует помнить, что эффективная ставка всегда больше номинальной ставки (которую также называют объявленной процентной ставкой): 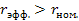 .
.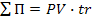 (2.2)
(2.2)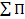 – сумма простых процентов,
– сумма простых процентов, 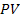 – первоначальная сумма вклада по настоящей стоимости,
– первоначальная сумма вклада по настоящей стоимости,  – продолжительность инвестирования,
– продолжительность инвестирования,  – процентная ставка (в долях единицы).
– процентная ставка (в долях единицы).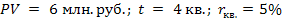
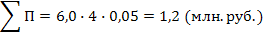
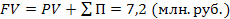
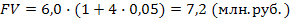
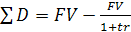 (2.3)
(2.3)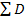 – сумма дисконта за обусловленный период инвестирования,
– сумма дисконта за обусловленный период инвестирования, 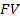 – конечная сумма вклада (капитала),
– конечная сумма вклада (капитала), 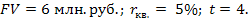
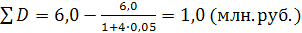
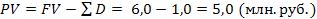 .
.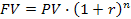 (2.4)
(2.4) (2.5)
(2.5)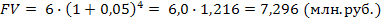
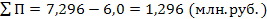
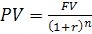 (2.6)
(2.6)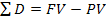 (2.7)
(2.7)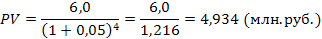
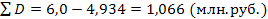
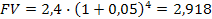
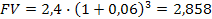
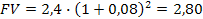

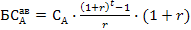 (2.8)
(2.8) – член аннуитета, характеризующий сумму отдельного платежа;
– член аннуитета, характеризующий сумму отдельного платежа; 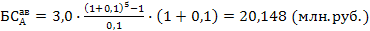
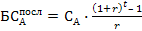 (2.9)
(2.9)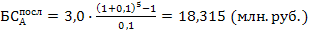
 (2.10)
(2.10)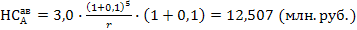
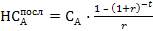 (2.11)
(2.11)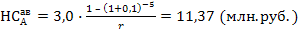
 (2.12)
(2.12)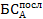 – будущая стоимость аннуитета, осуществляемого на условиях последующих платежей.
– будущая стоимость аннуитета, осуществляемого на условиях последующих платежей.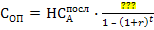 (2.13)
(2.13)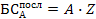 (2.14)
(2.14)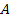 – сумма отдельного аннуитетного платежа;
– сумма отдельного аннуитетного платежа; 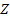 – множитель наращения аннуитета, определяемый по специальным расчетным таблицам с учетом ставки процента и числа периодов.
– множитель наращения аннуитета, определяемый по специальным расчетным таблицам с учетом ставки процента и числа периодов.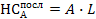 (2.15)
(2.15)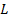 – дисконтный множитель аннуитета, определяемый по специальным расчетным таблицам с учетом ставки процента и числа периодов.
– дисконтный множитель аннуитета, определяемый по специальным расчетным таблицам с учетом ставки процента и числа периодов.


