
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Визначення місця знаходження точки на земній кулі.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
У першому наближенні Землю можна вважати кулею. Ближче до істинної фігури Землі буде еліпсоїд обертання, одержаний обертанням еліпса навколо його малої осі. Якщо позначити через а і b найбільшу та найменшу півосі еліпсоїда, то стиснення f виразиться формулою Прийнято характеризувати фігуру Землі наступними параметрами еліпсоїда обертання: Положення будь-якого пункту на поверхні Землі, визначається двома координатами: широтою Вісь обертання Землі перетинає її поверхню у двох точках: північному N і південному S полюсах. Площина, що проходить через центр Землі перпендикулярно до осі обертання називається екваторіальною площиною. Лінія QQ, утворена перетином поверхні Землі екваторіальною площиною, називається земним (географічним) екватором, який поділяє поверхню Землі на дві півкулі: північну (з північним полюсом N) і південну (з південним полюсом S). Малі круги, паралельні земному екватору, називають географічними паралелями (рис. 10). За початкову (нульову) паралель, від якої ведуть рахунок географічної широти, прийнято географічний екватор. Примітка. Географічні паралелі, які відстоять на Коло, що проходить через полюси N і S і дану точку М, називають географічним меридіаном точки М. Всі меридіани є великі кола. У міжнародній практиці за початковий (нульовий) меридіан, від якого ведуть рахунок географічної довготи, прийнято меридіан Гринвіча. Широтою Розрізняють північну (N) та південну (S) широти, Довготою
Розрізняють східну (О) та західну (W) довготу.
Земля повертається з заходу на схід з рівномірною швидкістю і за 24 години повертається 1 раз навколо своєї осі або на Визначення географічної довготи можна здійснювати за допомогою годинника, який показує час за Гринвічем. Якщо в деякому пункті, довготу якого треба визначити,за місцевим часом 12 год, а на годиннику, що показує час за Гринвічем, 14год. 5хв., то це означає, що в цьому пункті опівдні за Гринвічем було 2 год. 5 хв. тому назад. Значить даний пункт знаходиться на Якщо у даному пункті опівдні годинник показує 10год. 57хв за Гринвічем, то це означає, що за Гринвічем годинник покаже опівдні через 1год. 3 хв., а значить його довгота становить Обчислення градусної міри сторін і кута одержаного сферичного трикутника та відстані між двома пунктами Найкоротшою відстанню між двома точками сфери є довжина дуги великого кола, яка проходить через ці точки і менша 1800. Тобто L=Rα, де α-радіанна міра дуги, а R- радіус сфери. При обчисленні найкоротшої відстані між пунктами, доцільно користуватись наступними співвідношеннями:
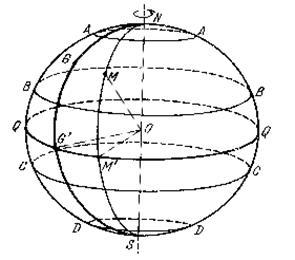
Кут FNA=
Рис.11. Рис. 11 Розв’язування задач. Задача: Визначити найкоротшу відстань між пунктами О і R, якщо відомі їх координати. О: широта Розв'язання Найкоротша відстань між пунктами на Земній кулі є довжина дуги великого кола, яке проходить через обидва пункти і менша 1800. Позначимо полюси
Кут
Рис.12. Скористаємось теоремою косинусів сторін сферичного трикутника RON. Маємо:
Знайдене значення дає величину центрального кута, який відповідає дузі
IV. Питання для самоконтролю 1. Користуючись географічними координатами ( а) точки К(330N; 500O); M(400S; 600W); б) найкоротшу відстань між точками К та М. 2. Користуючись рис. 11, записати: а) міри кутів FNB, ANB, ANC б) міри сторін SC, SD трикутника 1) SDC; 2) DNC. 3. Записати теорему косинуса сторони DC сферичних трикутників DNC і DSC. 4. Сформулювати план: а) побудови дуги великого кола, що проходить через точки C і D; б) обчислення довжини дуг DN і SE. 5. У яких випадках: а) кут у полюса сферичного трикутника дорівнює: 1) б) градусна міра сторони сферичного трикутника дорівнює: а)
V. Література 1. Андронов И.К., Окунев А.К., Курс тригонометрии „ Пособие для учителей ”- М: Просвещение, 1967, – 648с., (483-486 с.). 2. Кранц П., Сферическая тригонометрия – М. 2007, – 93с., (26-33 с.). 3. Куликов К.А., Курс сферической астрономии – Изд-во Наука, - М. 1969- 216 с. (10-12 с.)
|
|||||||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 472; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.14.133.188 (0.009 с.) |

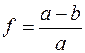 .
.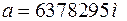 ,
, 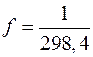 . В дійсності Земля за своєю формою значно складніша. Для простоти зображення будемо вважати земну поверхню сферою.
. В дійсності Земля за своєю формою значно складніша. Для простоти зображення будемо вважати земну поверхню сферою.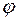 і довготою
і довготою 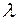 . При цьому основним напрямом є напрям осі обертання Землі, який співпадає з найменшою віссю еліпсоїда.
. При цьому основним напрямом є напрям осі обертання Землі, який співпадає з найменшою віссю еліпсоїда.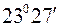 на північ і на південь від екватора, називаються тропіками. Тропіки обмежують жаркий кліматичний пояс Землі. Географічні паралелі, які відстоять на
на північ і на південь від екватора, називаються тропіками. Тропіки обмежують жаркий кліматичний пояс Землі. Географічні паралелі, які відстоять на 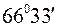 від екватора, вважаються межами холодних і помірним кліматичних поясів і називаються північним і південним полярними кругами.
від екватора, вважаються межами холодних і помірним кліматичних поясів і називаються північним і південним полярними кругами.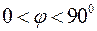 (Рис. 10).
(Рис. 10).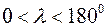
 а)
а)
 б)
б)
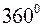 , тобто, за 1 годину – на
, тобто, за 1 годину – на 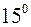 , або за 1 хвилину - на
, або за 1 хвилину - на 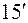
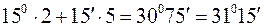 на захід, а його довгота становить
на захід, а його довгота становить 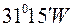 .
.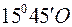 .
.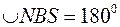 ,
, 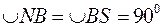 ,
, 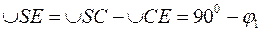 ,
, 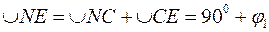 . (рис. 11)
. (рис. 11) , кут BNC=
, кут BNC= 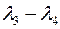 , тому що
, тому що 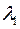 і
і 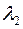 (
(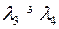 ), є західні довготи (східні), тобто відкладаються в одному напрямі від меридіана Гринвіча. Кут ANB=
), є західні довготи (східні), тобто відкладаються в одному напрямі від меридіана Гринвіча. Кут ANB= 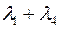 , бо
, бо 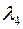 відкладають у різних напрямках відносно меридіана Гринвіча (рис 11).
відкладають у різних напрямках відносно меридіана Гринвіча (рис 11).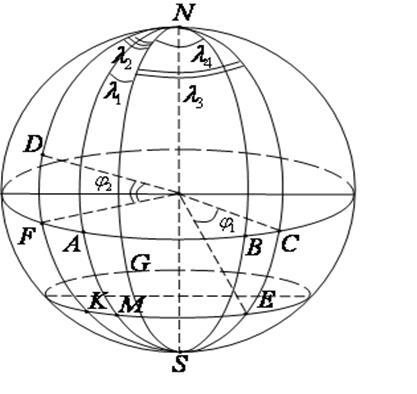
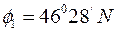 , довгота
, довгота 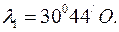 R: широта
R: широта 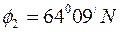 , довгота
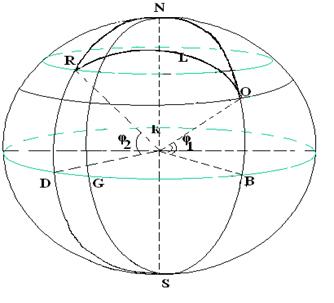
, довгота  (Рис. 12)
(Рис. 12)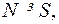 Меридіани
Меридіани 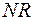 та
та 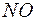 , які проходять через точки
, які проходять через точки 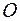 та
та 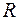 , та побудуємо дугу великого кола, що проходить через ці ж точки. Утворився сферичний трикутник NRO.
, та побудуємо дугу великого кола, що проходить через ці ж точки. Утворився сферичний трикутник NRO. 
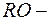 найкоротша відстань між О та R.
найкоротша відстань між О та R. 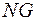 – нульовий меридіан (меридіан Гринвіча). Дуга NR доповнює
– нульовий меридіан (меридіан Гринвіча). Дуга NR доповнює 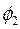 до
до 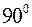 , а
, а 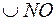 доповнює
доповнює 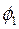 до
до 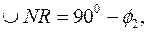
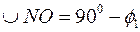 .
.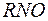 є сумою довгот λ1 та λ2 тобто λ1 +λ2, бо довгота λ1 східна, а λ2 - західна.
є сумою довгот λ1 та λ2 тобто λ1 +λ2, бо довгота λ1 східна, а λ2 - західна.



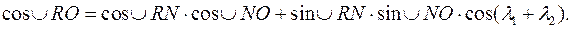
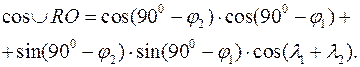
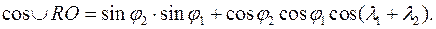
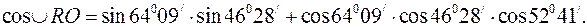
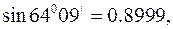

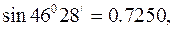
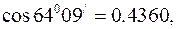
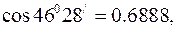
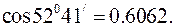
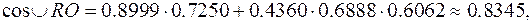
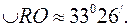
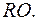 Відомо, що довжина дуги
Відомо, що довжина дуги 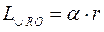 , де
, де 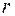 - радіус земної кулі,
- радіус земної кулі, 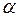 - радіанна міра центрального кута, який відповідає дузі
- радіанна міра центрального кута, який відповідає дузі 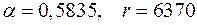 км. Одержимо
км. Одержимо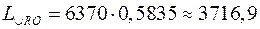 (км). Відповідь: 3716,9 км.
(км). Відповідь: 3716,9 км.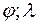 ) побудувати:
) побудувати: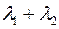 ?; 2)
?; 2) 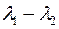 ?.
?.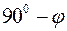 ?, б)
?, б) 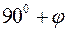 ?
?


