
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Площу сферичного трикутника обчислюють за формуламиСодержание книги
Поиск на нашем сайте
(1) (2) Сума кутів сферичного трикутника
6. Побудова трикутника на сфері: а) за трьома сторонами; б) за трьома кутами а). Побудувати на сфері трикутник за трьома сторонами Розв'язання. Перевіримо, чи існує сферичний трикутник з такими сторонами. Відомо, що для існування сферичного трикутника повинні виконуватись наступні умови: а) б) в) г) Умови а-г виконані, значить сферичний трикутник може існувати.. Хід побудови. 1. Вибираємо довільний радіус 2. Будуємо коло, що відповідає колу великого круга на сфері (рис.7а). Нехай О1 А1 = R
а) б) Рис. 7 3. Від радіуса О1 А1 відкладаємо центральні кути 4. Будуємо сферу радіуса 5. Вимірявши циркулем хорду 6. Опишемо на сфері радіусом 7. Будуємо полюси S,T,F відповідно дуг АВ, АС, ВС. 8. На сфері будуємо дуги великих кіл, що проходять через точки А та В, А та С, В та С. Одержимо сферичний трикутник АВС.
б). Побудувати сферичний трикутник за трьома кутами А, В та С. План побудови. 1 Перевірити, чи існує сферичний трикутник з такими кутами. 2. Обчислити сторони 3. Побудувати трикутник 4. Побудувати полюси дуг А1В1, А1С1, В1С1. Це будуть точки С, В та А – вершини шуканого трикутника.. 5. Побудувати дуги великих кіл, які проходять через точки 7. Довести нерівності: а)
ІV. Питання для самоконтролю. 1. Назвати поняття, які були введені в лекції. Дати їх визначення. 2. Що називається сферичним трикутником? 3. Що є мірою кутів (сторін) сферичного трикутника? 4. Користуючись зображенням на сфері трьох великих кіл (рис.5), назвати: а) суміжні сферичні трикутники; б) симетричні сферичні трикутники; в) сферичний перпендикуляр до дуги, яку називає викладач; г) чи є серед сферичних трикутників, зображених на сфері, прямокутні? 5. Сформулювати властивості кутів і сторін суміжних та симетричних трикутників. 6. Сформулювати умови існування косокутних (прямокутних) сферичних трикутників? 7. Що можна сказати про величину третьої сторони сферичного трикутника, якщо а =1300, b =1000 ? 8. Які сферичні трикутники називають взаємно полярними? 9. Записати співвідношення між сторонами і кутами взаємно полярних трикутників. 10. Трикутники б) сферичний надлишок. 11. Довести, що 12. Записати формулу для обчислення площі сферичного трикутника. 13. Обчислити площу сферичного трикутника АВС, якщо: а) Ð А=1320, ÐВ=740, ÐС=1000; б) 14. Сформулювати план побудови трикутника на сфері: а) за трьома сторонами; б) за трьома кутами. V. Література. 1. Андронов И.К., Окунев А.К., Курс тригонометрии «Пособие для учителей» - М: Просвещения, 1967,– 648 с., (488-494 с.). 2. Волынский Б.А. Сферическая тригонометрия – М.Наука 1977,– 136 с., (25-34 с.). 3. Кранц П., Сферическая тригонометрия – М. 2007,– 93 с. (10-15, 79-81 с.).
Лекції 4-5. Тема: Основні формули сферичної тригонометрії І. План лекції. 1. Теорема синусів. 2. Теореми косинусів сторін сферичного трикутника. 3. Теореми косинусів кутів сферичного трикутника. 4. Наслідки з теорем синусів та косинусів.
ІІ. Основні типи задач 1. Розпізнавати записані співвідношення між елементами сферичного трикутника. 2. Читати (змістовно) записану тотожність. 3. Формулювати критерії застосування кожної тотожності. 4. Одержувати з однієї тотожності дві інші за допомогою кругової перестановки букв. ІІІ. Короткі теоретичні відомості. Теорема синусів. Виведемо залежності між сторонами і кутами сферичного трикутника. На сфері з центром в точці О візьмемо сферичний трикутник АВС (рис. 8) зі сторонами а, b, c. З’єднаємо вершини сферичного трикутника А, В і С з центром сфери О радіусами ОА=ОВ=ОС=R. Опустимо з вершини С сферичного трикутника перпендикуляр СЕ на площину АОВ. У площині АОВ з точки Е проведемо ED Центральні кути СОК, COD i КOD чисельно дорівнюють відповідним їм дугам a, b i c. КутА сферичного трикутника АВС дорівнює двогранному куту CDE. Аналогічно, Ð В = Ð СКЕ. Використовуючи співвідношення між сторонами і кутами плоских прямокутних трикутників можна одержати співвідношення між сторонами і кутами сферичного трикутника.
Рис. 8
Δ ЕСК і Δ ОСК: ЕС = СК sin B = R sin a sin B, Δ ECD і Δ ОСD: EC = CD sin A = R sin b sin A. Прирівнюючи між собою праві частини цих рівностей, одержимо першу формулу групи (1). Останні дві формули записують по аналогії.
Формули групи (1) називають формулами синусів записують:
2. Теореми косинусів сторін. Запишемо очевидну рівність: ОК = ОМ + МК. Виразимо відрізки ОК, ОМ і МК через тригонометричні функції кутів і сторін плоских трикутників: КОС, MOD, DOC, NDE і ECD, а саме Δ ОКС: ОК = R cos а, Δ OMD, Δ COD: OM=OD cos c = R cos b cos c, Δ NED, ΔCOD, ΔCDE: MK = NE = ED sin c = CD cos A sin c = R sin b sin c cos A Підставимо замість ОК, ОМ і МК їх значення. Одержимо першу формулу групи (2). Останні дві формули записують по аналогії.
Формули (2) іноді називають формулами косинусів сторін і читають так: у будь-якому сферичному трикутнику косинус сторони дорівнює добутку косинусів двох інших сторін доданого до добутку синусів тих же сторін, помноженого на косинус кута між ними. 3. Теореми косинусів кутів. Застосуємо формули групи (2) до трикутника, полярного даному.
Одержимо формули групи (3), які називають формулами косинусів кутів.
Тобто, у будь-якому сферичному трикутнику косинус кута дорівнює добутку косинусів двох інших кутів, взятому зі знаком «-», доданого до добутку синусів цих же кутів, помноженого на косинус сторони між ними. 4. Наслідки з теорем синусів та косинусів. Запишемо ще одну очевидну рівність: MN=MD-ND. Оскільки, MN=KE=KC cosB=R sin а cosB, MD=OD sinc=R cosb sinc, ND=ED cosc=DC cosA cosc=R sinb cosc cosA. Замість MN, MD і ND підставимо їх значення. Одержимо
Скориставшись правилом кругової заміни, одержимо формули групи (4’)
Одержані рівності читають так: у будь-якому сферичному трикутнику добуток синуса сторони на косинус прилеглого кута дорівнює добутку косинуса на синус двох інших сторін мінус добуток синуса на косинус цих же сторін, помноженого на косинус кута між ними. На основі властивостей взаємно полярних трикутників,
Якщо формулу з групи (4) поділити почленно на формулу групи (1), у лівій частині якої ті самі елементи, то одержимо формулу котангенсів, що містить дві сторони і два кути.
Формули групи (6) називають формулами котангенсів. Вони містять дві сторони і два кути, тому їх називають формулами чотирьох елементів. Перетворимо одержані формули для прямокутних сферичних трикутників Якщо, в групах формул (1)-(6) прийняти один із кутів, наприклад С, рівним 900, то формули матимуть вигляд: для групи (1)
для групи (2)
для групи (3)
для груп (4) і (4’)
для групи (5)
Група (6) нових формул не дає. Для запам’ятовування формул прямокутного сферичного трикутника існує правило Непера.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 772; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.227.73 (0.01 с.) |

 , де R-радіус сфери;
, де R-радіус сфери; , де
, де  - сферичний надлишок. (3)
- сферичний надлишок. (3) . (4).
. (4). та
та  , якщо
, якщо  ,
,  .
. ,
,  ;
; ,
,  ;
; ,
,  ;
; .
.  .
. сфери.
сфери.
 ,
,  ,
,  та з'єднуємо між собою хордами точки
та з'єднуємо між собою хордами точки  та
та  ,
,  та
та  , С1 та D1.
, С1 та D1.
 дуги с (рис. 7а), відмітимо на сфері дві точки
дуги с (рис. 7а), відмітимо на сфері дві точки  та
та  , відстань між якими
, відстань між якими  . (Дуга
. (Дуга  великого кола дорівнює дузі с, так як рівним хордам одного й того ж кола відповідають рівні центральні кути).
великого кола дорівнює дузі с, так як рівним хордам одного й того ж кола відповідають рівні центральні кути).
 коло з центром в т.
коло з центром в т.  та радіусом
та радіусом 
 - коло з центром в т.
- коло з центром в т.  .
. 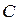 - точка перетину цих кіл.
- точка перетину цих кіл. ,
,  ,
,  трикутника
трикутника 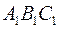 , полярного до трикутника
, полярного до трикутника  .
. ;
; 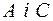 ;
;  . Трикутник
. Трикутник  ; б)
; б) 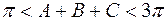 .
. та
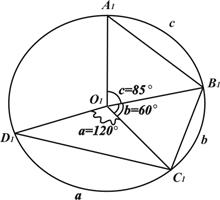
та 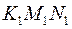 --взаємно полярні. Знайти: а) сторони трикутника
--взаємно полярні. Знайти: а) сторони трикутника 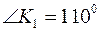 ,
, 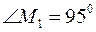 ,
,  ;
; .
. .
. АО і ЕК
АО і ЕК 

 – і читають так – синуси сторін сферичного трикутника пропорційні синусам протилежних кутів.
– і читають так – синуси сторін сферичного трикутника пропорційні синусам протилежних кутів.





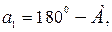
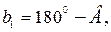
 , одержимо групу формул (5)
, одержимо групу формул (5)

 ,
,  .
. (7)
(7) ,
, . (8)
. (8) (9)
(9)
 (10)
(10)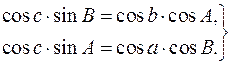 (11)
(11)
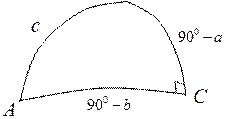
 ). Кожен катет (
). Кожен катет (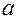 та
та  ) замінимо їх доповненнями до
) замінимо їх доповненнями до 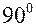 (
( та
та  ). Прямий кут С не будемо приймати до уваги.
Кожен з елементів (с, А, В,
). Прямий кут С не будемо приймати до уваги.
Кожен з елементів (с, А, В, 


