
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Співвідношення між елементами прямокутного сферичного трикутникаСодержание книги
Поиск на нашем сайте
1) 2) 3) 4)
5)
ІV. Питання для самоконтролю. 1. Записати теорему косинусів для сторони в(а;с). 2. Записати теорему косинусів кутів. 3. Як із формул групи (4), одержати формули групи 4’? 4. Сформулювати алгоритм одержання формул групи (5) (групи (6)). 5. Сформулювати правило Непера запам’ятовування формул для прямокутного сферичного трикутника. Література 1. Андронов И.К., Окунев А.К., Курс тригонометрии „Пособие для учителей” - М: Просвещения, 1967, – 648 с., (483-486, 510-512 с.). 2. Волынский Б.А. Сферическая тригонометрия – М.Наука 1977, – 136 с., (43-55 с.). 3. Кранц П., Сферическая тригонометрия – М. 2007, – 93 с., (15-20, 25-26, 55-56 с.). 4. Куликов К.А., Курс сферической астрономии – Изд-во Наука, - М. 1969- 216 с. (31-36 с.) Лекції 6-7. Тема: Розв'язання сферичних трикутників. І. План лекції. 1. Послідовність операцій при розв'язанні сферичних трикутників. 2. Основні типи задач на розв'язання довільних сферичних трикутників. Розв'язання сферичних трикутників за: а) трьома сторонами; б) трьома кутами; в) двома сторонами та кутом між ними. 3. Шість основних типів задач розв'язання прямокутних сферичних трикутників. 4. Приклади розв’язування сферичних трикутників. ІІ. Основні типи задач. 1. Перевірка існування сферичного трикутника за даними елементами. 2. Розв'язання сферичних трикутників за: а) трьома сторонами; б) трьома кутами в) двома сторонами та кутом між ними; .3. Розв'язання прямокутних сферичних трикутників за: а) двома катетами; б) гіпотенузою та катетом; в) гіпотенузою та прилеглим кутом; г) катетом та протилежним кутом; д) катетом та прилеглим кутом; е) двома кутами, прилеглими до гіпотенузи.
ІІІ. Короткі теоретичні відомості. 1. Послідовність операцій при розв’язанні сферичних трикутників: 1. Оцінка вихідних даних. 2. Вибір формул для обчислення шуканих елементів. 3. Виконання обчислень. 4. Контрольні обчислення (обчислення однієї і тієї ж невідомої величини за двома різними формулами). 5. Аналіз одержаних результатів.
Розв’язання сферичних трикутників Таблиця 4
Шість основних типів задач розв'язання прямокутних сферичних трикутників
Приклади розв’язання задач а) Розв’язати сферичний трикутник, у якого: а = 790331 , b = 650281, с = 370531
Розв’язання Перевіримо, чи існує трикутник з такими сторонами. 00 < а = 790331 < 1800, 00 < b = 650281 < 1800, 00 < c = 370531 < 1800,
a+b = 790331 + 650281 = 1450011 > c = 370531, a+c = 790331 + 370531 = 1170261 > b = 650281,
b+c = 650281 + 370531 = 1030211 > a = 790331. Трикутник з такими сторонами може існувати.
Обчислення кута А. cosa = cosb cosc + sinb sinc cosA, cosa = cos 790331 = 0,1814, cosb = cos650281 = 0,4152, cosc = cos 370531 = 0,7893, cosb cosc =0,4152*0,7893= 0,3277, sinb = sin 650281 = 0,9097, sinc = sin 370531 = 0,6141, sinb sinc = 0,9097*0,6141=0,5586, cos a – cos b cos c = 0,1814 - 0,3277= - 0,1463,
A=arccos(-0,2619)=1800-arccos 0,2619=1050101. Обчислення кута В.
Обчислення кута С
Відповідь: б) Розв’язати сферичний трикутник, у якого Розв’язання. Перевіримо, чи існує сферичний трикутник з такими кутами:
Трикутник з такими кутами може існувати.
Обчислення сторони
Обчислення сторони
Обчислення сторони
Відповідь: в) Розв’язати сферичний трикутник у якого:
Перевіримо, чи існує сферичний трикутник з такими елементами.
Отже, з такими даними сферичний трикутник може існувати.
Обчислення катета а.
Обчислення кута В:
Відповідь: ІV. Питання для самоконтролю. 1. Сформулювати послідовність дій при розв’язанні сферичного трикутника. 2. Навести приклади задач, за даними яких сферичний трикутник: а) не існує; б) існує. 3. Чи існує сферичний трикутник, кути якого дорівнюють: а) А=150, В=250, С=960? б) А=700, В=300, С=800? в) А=1040, В=830, С=150? 4. За яких даних слід застосовувати: а) теорему косинусів сторін; б) формули чотирьох елементів; в) теореми косинусів кутів.
5.Чи існує трикутник з такими сторонами: а) 6. Записати формули, за якими можна обчислювати кути сферичного трикутника.
Література 5. Андронов И.К., Окунев А.К., Курс тригонометрии „Пособие для учителей” - М: Просвещения, 1967, – 648 с., (488-491 с.). 6. Волынский Б.А. Сферическая тригонометрия – М.Наука 1977, – 136 с., (85-90 с.). 7. Кранц П., Сферическая тригонометрия – М. 2007, – 93 с., (51-61 с.). 8. Куликов К.А., Курс сферической астрономии – Изд-во Наука, - М. 1969- 216 с. (31-36 с.)
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 550; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.103.13 (0.008 с.) |

 ;
;  ;
;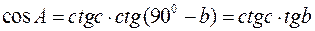 ;
;  ;
; ,
,  ;
; ;
; ;
; ;
;








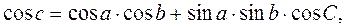



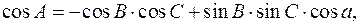
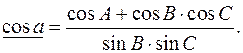





 ,
кути
,
кути 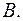
 (6):
(6): 
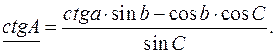



 ,
кути
,
кути  (6):
(6): 




 ,
кути
,
кути 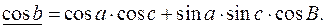 (6):
(6): 





 кути
кути 
 (8):
(8): 
 звідки
(6):
звідки
(6): 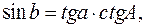 тоді
тоді  (6):
(6): 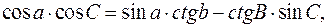 звідки
звідки
 тоді
тоді 
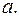
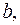 кути
кути 
 З (7):
З (7):  , тоді
, тоді 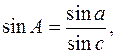 З (4):
З (4):  Тоді
Тоді 

 кут
кут 
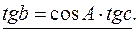 З (7):
З (7):  З (3):
З (3): 


 З (7):
З (7):  З (3):
З (3):  тоді
тоді

 ,
,  З (10):
З (10): 
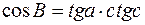 ,
З (10):
,
З (10):  ,
З (9)
,
З (9) 
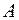 та
та 
 З (9):
З (9): 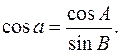 З (9):
З (9): 


 ,
,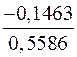 = -0,2619,
= -0,2619, ,
,
 0,4152,
0,4152,
 0,1814,
0,1814,
 0,7893,
0,7893,
 0,1432,
0,1432,
 0,272,
0,272,
 0,9834,
0,9834,
 0,6141,
0,6141,
 0,6039,
0,6039,
 ,
,

 ,
,
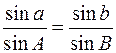 , звідки
, звідки
 ,
,
 0,9834*0,8928=0,8780,
0,9834*0,8928=0,8780,
 0,9097*0,9652=0,8781,
Обчислення виконано правильно, залишається лише перевірити, чи існує трикутник з такими даними.
0,9097*0,9652=0,8781,
Обчислення виконано правильно, залишається лише перевірити, чи існує трикутник з такими даними.
 ,
,
 0,0753,
0,0753,
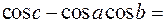 0,714,
0,714,
 0,9097
0,9097
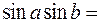 0,8946,
0,8946,
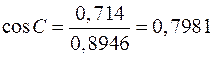 ,
,
 .
.
 , звідки
, звідки
 ,
,
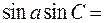 0,9834*0,6025=0,5925,
0,9834*0,6025=0,5925,
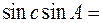 0,6141*0,9652=0,5927,
Обчислення виконано правильно, залишається лише перевірити, чи існує трикутник з такими даними.
(Перевірку виконати самостійно)
0,6141*0,9652=0,5927,
Обчислення виконано правильно, залишається лише перевірити, чи існує трикутник з такими даними.
(Перевірку виконати самостійно)
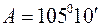 ,
,  ,
, 
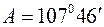 ,
,  ,
, 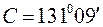 .
. ,
,  ,
, ,
, ,
, ,
, ,
, .
. ,
,  -0,3051,
-0,3051, 0,3469,
0,3469,  -0,6580,
-0,6580,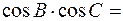 -0,2283,
-0,2283,  -0,3051-0,2283=-0,5334,
-0,3051-0,2283=-0,5334, 0,9379,
0,9379,  0,7530,
0,7530, 0,7062,
0,7062,  -0,7553,
-0,7553,
 ,
,
 0,2008,
0,2008,
 0,5477,
0,5477,
 0,9523,
0,9523,
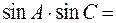 0,7171,
0,7171,
 0,7638,
0,7638,
 .
.
 ,
,
 0,9523*0,6455=0,6147.
Обчислення виконано правильно, залишається лише перевірити, чи існує трикутник з такими даними.
0,9523*0,6455=0,6147.
Обчислення виконано правильно, залишається лише перевірити, чи існує трикутник з такими даними.

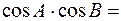 -0,1058,
-0,1058,
 -0,7638,
-0,7638,
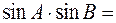 0,8932,
0,8932,
 -0,8551,
-0,8551,
 .
.

 ,
,
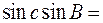 0,5185*0,9379=0,4863,
0,5185*0,9379=0,4863,
 0,7530*0,6455=0,4861,
Обчислення виконано правильно, залишається лише перевірити, чи існує трикутник з такими даними.
(Перевірку виконати самостійно)
0,7530*0,6455=0,4861,
Обчислення виконано правильно, залишається лише перевірити, чи існує трикутник з такими даними.
(Перевірку виконати самостійно)
 ,
,  ,
,  .
. ,
,  ,
,  .
. ,
,  ,
,  .
. ,
,
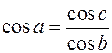 ,
(1)
,
(1)  ,
,
 ,
(4)
,
(4)  ,
,
 .
.
 ;
; ;
; ,
, ,
, ,
, ,
, ,
, або
або  ,
, ;
;
 ;
;


 ,
,

 , отже
, отже
 .
Значить
.
Значить  – сторонній розв’язок.
Або оскільки
– сторонній розв’язок.
Або оскільки  ,
то
,
то  має бути більшим
має бути більшим  .
Тому
.
Тому 
 ,
,

 ;
;
 .
Розв’язки знайдені правильно.
.
Розв’язки знайдені правильно.
 ,
,  ,
,  б)
б)  в)
в) 



