
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Каковы механические характеристики пластичных металлов при переменных нагрузках? как выбрать допускаемые напряжения для циклически нагруженных металлов?Содержание книги
Поиск на нашем сайте
Каковы механические характеристики прочности и пластичности металлов? как определить допускаемые напряжения для расчетов деталей машин из пластичных материалов, работающих при постоянных и переменных нагрузках? МЕХАНИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПРОЧНОСТИ И ПЛАСТИЧНОСТИ МЕТАЛЛОВ Пластичность – способность материала без разрушения получать большие остаточные деформации. Прочность – способность материала детали сопротивляться разрушению или образованию пластических деформаций под действием внешних нагрузок. Характеристики: - предел текучести σт или τт (при кручении) → при расчетах на прочность при постоян напр дм из пластичных материалов; напряжение при котором происходит рост деформации без заметного увеличения нагрузки. - предел прочности σв или τв→ при постоянных напряжениях из хрупких материалов; отношение макс силы, которую способен выдержать образец, к его начальной площади поперечного сечения. - предел выносливости σ R или τ R → при переменных напряжениях; макс напряжение при циклической нагрузке под действием которой не происходит усталостного разрушения после произвольного большого или заданного циклов нагружения. - предел выносливости σ - 1 или τ - 1→ при симметричном цикле. - предел пропорциональности – макс напряжение, при котором конструкция может работать без остаточных напряжений. ОПРЕДЕЛЕНИЕ ДОПУСКАЕМЫХ НАПРЯЖЕНИЙ ДЛЯ РАСЧЕТОВ ДМ ИЗ ПЛАСТИЧНЫХ МАТЕРИАЛОВ, РАБОТАЮЩИХ ПРИ ПОСТОЯННЫХ И ПЕРЕМЕННЫХ НАГРУЗКАХ Допускаемые напряжения [σ] и [τ] определяются по формулам: [σ]= σпред/[S]; [τ]= τпред/[S], где σпред и τпред – соответственно предельные нормальное и касательное напряжения, [S] – допускаемый коэффициент запаса прочности. При расчетах на прочность при постоянных напряжениях ДМ из пластичных материалов в качестве предельного напряжения σпред и τпред принимают соответствующий предел текучести: σт или τт . При расчете на прочность дм при переменных напряжениях в качестве предельного напряжения σпред и τпред принимают соответствующий предел выносливости: σ R – при изгибе, σ R р – при растяжении (сжатии), τ R – при кручении. Допускаемый коэф. запаса прочности [S]= [S1] [S2] [S3], где [S1] – коэф, учитывающий точность определения действующих на деталь нагрузок и возникающих в ней напряжений; [S2] – коэф, учитывающий однородность материала детали; [S3] - коэф, учитывающий специфические требования безопасности рассчитываемой дет. При точном расчете [S1]=1, при расчетах сред точности – 1,2…1,6. Коэф [S2] для стальных дет из поковок и проката равен 1,2…1,5; для деталей из стального литья – 1,5…1,8; для чугунных деталей – 1,5…2,5. Коэф [S3]=1…1,5.
Каковы механические характеристики пластичности материалов? по какому параметру делят все материалы на хрупкие и пластичные? к какой характеристике можно отнести твердость: к прочности или к пластичности? как определить допускаемые напряжения при статической нагрузке на деталь? Пластичность – способность материала без разрушения получать большие остаточные деформации. Характеристики пластичности: -модуль продольной упругости, или модуль Юнга(Е), который предложил назвать модулем лондонский врач Томас Юнг в 1807г. -модуль объемной упругости(μ), был впервые получен французским математиком, механиком и физиком Симеоном Дени Пуассоном, чье имя и носит в настоящее время: коэффициент Пуассона. Коэф. Пуассона вычисляют по зависимости μ=ε1/ε2, где ε1-относительное поперченное сжатие, ε2-относительное удлинение, для всех сталей μ=0,3 - относительное удлинение после разрыва (δ, %) – приращение расчетной длины образца после разрыва к ее первоначал длине. δ = (Dl/ l0) 100%= ((lк - l0)/ l0) 100%, где Dl- изменение длины образца в момент его разрыва, l0 -начальная длина образца. Относительное удлинение очень важная характеристика металла: по ее величине можно характеризовать металл как пластичный (δ≥5%) и хрупкий (δ<5%). - относительное сужение после разрыва(ψ, %) – отношение уменьшения площади попереч сеч-я образца в месте разрыва к начал площади попереч сеч-я. ψ= (DА / А0) 100%=((А - А0)/ А0) 100%, где DА-изменение площади поперечного сечения образца после разрыва, А0-начальная площадь поперченного сечения образца. Так же пластичность можно охарактеризовать: - относительное предельное равномерное удлинение (δр, %) – наибольшее удлинение, до кот образец деформируется равномерно по всей его расчетной длине. δр = (Dlp / l0) 100%. - относительное предельное равномерное сужение (ψр, %) – наибольшее сужение, до кот образец деформируется равномерно по всей его расчетной длине. ψр= (DFp / F0) 100% - относительное сужение после разрыва(ψ, %) – отношение уменьшения площади попереч сеч-я образца в месте разрыва к начал площади попереч сеч-я. ψ= (DFк / F0) 100%=((Fк - F0)/ F0) 100% Мерой пластичности материала явл-ся удлинение δ при разрыве. Чем она больше, тем пластичнее материал. Св-во, противоположное пластичности – хрупкость – способность мат-ла разрушаться без обр-я заметных остаточных деформаций. Для таких мат-лов удлинение при разрыве не превышает 2 – 5%. Твердость можно отнести как к характеристикам пластичности, так и к характеристикам прочности. Твердость – способ-ть мат-ла противодействовать мех проникновению в него посторонних тел (повторяет характеристику прочности). В мат-ле при вдавливании в него постороннего тела возникают местные пластич деформации, сопровождающиеся при дальнейшем увеличении сил местным разрушением. Поэтому пок-ль твердости связан с пок-лями прочности и пластичности и зависит от конкрет усл-ий ведения испытаний. Твердость выражают в единицах Бринеля, Роквелла, Виккерса и Шора. Единицы твердости по по Бринелю обозначают буквами “НB”. Измерение твердости материала осуществляют вдавливанием в течение 1с шарика диаметром 10 мм (2,5 или 5,0 мм) с последующим расчетом по формуле:
где F – стандартная сила вдавливания шарика, F =30000 Н; d – диаметр шарика, мм; h – глубина отпечатка, мм. Единицы твердости по Роквеллу обозначают буквами “ HRCЭ ”. Измерение твердости черных металлов осуществляют вдавливанием алмазного конуса с углом при вершине в 120° и с усилием в 1500 Н. Дня измерения твердости легких сплавов применяют шарик диаметром 1,588 мм (1/16 дюйма). При этом, если усилие вдавливания шарика равно1000 Н, то твердость обозначают буквами “ HRB”, а если усилие составляет600 H, то буквами “ HRА”. Единицы твердости по Виккерсу обозначают буквами “ HV”. Измерение твердости осуществляют вдавливанием в испытуемый материал алмазной пирамиды. Единицы твердости по Шору обозначают буквами “ НСd ”. Измерение твердости производят по высоте отскакивания легкого бойка с алмазным наконечником от испытуемого массивного образца. Метод назван по имени американского промышленника А. Шора.
Под воздействием внешних сил в материале детали возникают статические или циклические напряжения (нормальные или касательные). Если напряжения, достигнув некоторой величины, остаются неизменными по величине и знаку во время действия вызвавшей их нагрузки, то они называются статическими или нагрузкой I режима, или циклом I режима Отличительные признаки нагрузки I режима: σmax = σmin = σ a = σm, где σmax, σmin – наибольшее и наименьшее значения напряжений цикла; σ a, σm – амплитудное и среднее значение напряжений цикла. В литературе обозначение напряжений I режима не имеет индекса. Допускаемые напряжения [σ] и [τ] опред по формулам: [σ]= σпред/[S]; [τ]= τпред/[S], где σпред и τпред – предельные норм и касат напряжения, [S] – допускаемый коэф запаса прочности: [S]= [S1] [S2] [S3], где [S1] – коэф, учитывающий точность определения действующих на деталь нагрузок и возникающих в ней напряжений; [S2] – коэф, учитывающий однородность материала детали; [S3] - коэф, учит-щий специфич требования безопасности рассчитваемой дет. При точном расчете [S1]=1, при расчетах сред точности – 1,2…1,6. Коэф [S2] для стальных дет из поковок и проката равен 1,2…1,5; для деталей из стального литья – 1,5…1,8; для чугунных деталей – 1,5…2,5. Коэф [S3]=1…1,5.
Симметричные напряжения 1.Наибольшее и наименьшее напряжения равны по величине, но противоположны по знаку. 2.Среднее напряжение цикла Ассиметричные напряжения 1.Наибольшее и наименьшее напряжения равны по величине, по знаку могут быть одинаковы и противоположны. 2.Коэф-т ассиметрии R=-0,2.
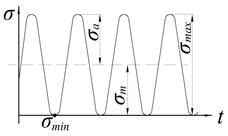
9. какие виды циклических нагрузок вам известны? назовите основные параметры, характеризующие циклическую нагрузку. Который цикл нагружения наиболее опасен для детали при равных максимальных значениях напряжений? Циклические сиЛы – это нагрузки, периодически изменяющиеся по направлению во времени. Как правило, по величине они не меняются (рис.2.3).
Вспомним, что цикл – это однократное изменение нагрузки во времени (при повторяющемся характере её значений); период цикла t0 – это время длительности одного цикла нагрузки. Если напряжения вызваны циклически изменяющейся нагрузкой, то они носят название циклических (переменных) напряжений. Все переменные напряжения делят на 3 вида: · пульсирующие (или II режима, или II цикла), · симметричные (или III режима, или III цикла), · асимметричные (или IV режима, или IV цикла). Все циклические напряжения характеризуют следующими параметрами: - наибольшим (по алгебраическому смыслу) значением напряжения σmax, τmax; - наименьшим (по алгебраическому смыслу) значением напряжения σmin, τmin; - средним (по алгебраическому смыслу) значением напряжения(2.1)
- амплитудным значением напряжения(2.2)
- коэффициентом асимметрии цикла(2.3): Rσ = σmin / σmax, Rτ = τmin / τmax, С учетом зависимостей (2.1), (2.2) и (2.3) можно получить соотношения напряжений для симметричного и отнулевого циклов (рис.2.6 и 2.7).
Отличительными признаками пульсирующих (отнулевых) напряжений являются: 1) σmin= 0; 2) σ a = σm= 0,5σmax 3) Rσ = 0
Отличительными признаками цикла симметричных напряжений являются: 1) σm= 0; 2) σ a = σm= σmax 3) Rσ = –1 В литературе обозначение этих напряжений снабжают индексом “–1 ”: σ–1или τ –1 Асимметричные напряжения (или напряжения IV режима, или IV цикла) отличаются от рассмотренных выше циклических напряжений тем, что значения σmax, σmin, σ a, σm и R σ могут быть как положительными, так и отрицательными, а также – могут быть целыми или дробными числами. В литературе обозначение этих напряжений снабжают индексом, соответствующим значению коэффициента асимметрии цикла “R ”: σRили τ R Симметричный цикл самый опасный (большая амлитуда—резонанс) По каким параметрам оценивают силу циклического напряжения? если сравнивать две циклические нагрузки, имеющие равные амплитудные значения, но разные средние значения цикла, то которая нагрузка опаснее для детали? Циклические хар-ся
Нулевые характеризуются Симметричные характеризуются / Асимметричные характеризуются
Нагрузка тем опаснее для детали, чем больше среднее значение цикла. Зубчатые цилиндрические косозубые и шевронные передачи: область применения, особенности нагружения, достоинства и недостатки в сравнении с прямозубой передачей. Понятие об эквивалентом цилиндрическом прямозубом колесе. Цилиндрические колеса, у которых зубья расположены по винтовым линиям на делительном цилиндре, называют косозубыми. В отличие от прямозубой в косозубой передаче зубья входят в зацепление не сразу по всей длине, а постепенно. Увеличивается время контакта одной пары зубьев, в течение кот-ого входят новые пары зубьев, нагрузка передается по большому числу контактных линий, что значительно снижает шум и динамические нагрузки. Осевая сила Fа дополнительно нагружает подшипники, возрастая с увеличением угла наклона зуба Шевронные колеса представляют собой сдвоенное косозубое колесо, выполненное как одно целое. Вследствие разного направления зубьев на полушевронах осевые силы взаимно уравновешиваются на колесе и на подшипники не предаются. Применяются в мощных быстроходных закрытых передачах. Недостатком шевронных колес является большая стоимость их изготовления. Из-за наклонного расположения зуба силу нормального давления для удобства анализа раскладывают на 3 составляющие: Выразим математически все составляющие силы нормального давления на зуб
У косозубых колес зубья располагаются не по образующей делительного цилиндра, а составляют с ней некоторый угол окружной шаг окружной модуль делительный диаметр Прочность зуба определяют его размеры и форма в нормальном сечении. Форму косого зуба в нормальном сечении принято определять через принято определять через параметры эквивалентного прямозубого колеса. Увеличение эквивалентных параметров с увеличением угла
Чтобы воспользоваться расчетными зависимостями, полученными для прямозубых цилиндрических передач с целью проектного и проверочного их расчета определим: 1. Какие размеры должно иметь цилиндр. прямозуб. колесо той же прочности, что и исходное косозубое колесо. Это прямозуб. колесо назовем эквивалентным. 2. Снабдим все параметры эквивал. колеса индексом V. Два колеса будут обладать равной прочностью, если их зубья будут иметь равны модули и равную длину.
15. Цилиндрические косозубые передачи: область применения, силы в зацеплении и нагрузки, действующие на валы. Достоинства и недостатки косозубых передач в сравнении с прямозубыми. Каков диапазон величин угла наклона зубьев в косозубых передачах и почему он таков? Различают правые и левые косозубые колеса в зависимости от направления винтовой линии зуба. При работе такой передачи зубья входят в зацепление не сразу по всей длине, как в прямозубой, а постепенно; передаваемая нагрузка распределяется на несколько зубьев. В результате по сравнению с прямозубой повышается нагрузочная способность, увеличивается плавность работы передачи и уменьшается шум. Поэтому косозубые передачи имеют преимущественное распространение. Сила нормального давления Fn, являющаяся результирующей мгновенных давлений, направлена по нормали к эвольвентной поверхности зуба. Для удобства анализа разложим пространственное усилие Fn на составляющие в системе координат, имеющей начало в полюсе зацепления, и направим одну составляющую Ft (окружную) вдоль вектора окружной, вторую Fr - по радиусу начальной окружности к центру колеса и третью составляющую Fа (осевую)-параллельно оси вращения колеса.
Сила Fn1, действующая на зуб шестерни (см. рисунок 24а), - реакция ведомого колеса, поэтому окружная сила Ft1 направлена навстречу движению шестерни и равна:
Нормальное усилие Fn всегда направлено в сторону центра вращения, поэтому и его радиальная составляющая также направлена к центру вращения:
Направление осевой силы Fa1 зависит от направления наклона зуба (правое или левое) (см. рисунок 24б): Fa1= Ft1 ∙ tgβ
Поскольку F2= Ft1 / cos dtw, то:
С учетом выражения окружного усилия через крутящий момент получим:
Достоинства косозубых передач:
где εdn, εdк - коэффициенты торцевого перекрытия соответственно в прямозубой и косозубой передачах; εdк = 1,2…1,5 при v < 3 м/c, εdк = 1,5…2,0 при v<3…15 м/c, εdк = 2…3 при v>15 м/c, 2.Благодаря наклонному расположению зубьев увеличивается 3. В связи с изменением профиля зуба в торцевом сечении Недостатки косозубых передач: 1. Линии мгновенного контакта располагаются не вдоль образующей зуба, а под углом λ к ней (рисунок 21). В результате в начальный момент зацепления колес вся нагрузка приложена со стороны одного из торцов, что приводит к концентрации нагрузки, понижению местной (в районе торца) изгибной прочности и к скалыванию зуба (см. рисунок 21). 2. Наклонное расположение зуба по отношению к торцу зубчатого колеса означает появление дополнительной (осевой) составляющей усилия зацепления Fa = Ft ∙ tgβ
Чем больше угол β, тем больше сила Fа, что приводит к повышению нагрузки на подшипники и к усложнению конструкций опорных узлов валов передачи. ГОСТ 2185-55 предусматривал значения β = 8...18°, при которых, с одной стороны, обеспечивается высокая плавность и нагрузочная способность передачи, а, с другой стороны - небольшая осевая сила Fa. Новый ГОСТ 2185-66 не предусматривает конкретных значений β, но рекомендации прежнего ГОСТа можно использовать при выборе угла β. Вместе с тем выполнение косозубого колеса с β<8° лишает его преимуществ по сравнению с прямозубым колесом. Увеличение угла β свыше 18° приводит к росту осевой составляющей Fa силы зацепления и, как следствие, к увеличению габаритных размеров опорных узлов валов передачи.
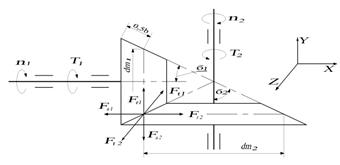
Зубчатые конические передачи: область применения, достоинства, недостатки. силы, действующие в зацеплении и на валы передачи. виды разрушения и условия прочности открытых и закрытых конических передач. Конические зубчатые колеса применяются для передачи вращения от одного вала к другому при пересекающихся осях. Межосевой угол Σ может изменяться от 10°до 170°. Наиболее часто он равен 90° (ортогональная передача), т.к. при других значениях этого угла значительно усложняется конструкция и технология изготовления корпусных деталей передач, хотя на изготовление самих колес величина межосевого угла Σ не влияет. Конические колеса выполняют с прямыми, косыми, круговыми и другими криволинейными зубьями Зуб передачу с пересекающимися осями, у кот началь и делительные пов-ти колес конические, наз конической. П/з конич перед: + простота изгот, монтажа и регулир-е по пятну контакта - оч чувствителны к ошибкам изгот-я и монтажа К/з конич перед: + плавность хода, более производит проц изгот-я, больше нагрузочная спос-ть Для удобства анализа сила нормального давления на зуб Fn может быть разложена на три взаимно перпендикулярные составляющие (на рис. 7.4).
Окружные силы Fti направлены по касательной к средней делительной окружности диаметром dmi. Для шестерни эта сила направлена навстречу её вращению. Для колеса окружная сила совпадает с направлением вращения колеса. Каждая окружная сила создаёт момент, противоположного знака относительно вращающего момента Ti,нагружающего вал. Радиальные силы Fri всегда направлены по радиусу от точки зацепления к оси колеса (шестерни). Осевые силы Fаi всегда направлены вдоль оси колеса (шестерни) от вершины конуса к его основанию. Соотношение сил в зацеплении конической передачи таково (см. рис. 7.4): Ft2 = – Ft1 Fr2 = – Fa1 Fa2 = – Fr1
Сила нормального давления на зуб конического колеса Fn2, перпендикулярна профилю зуба и приложена в полюсе зацепления (рис. 7.5). Одновременно сила Fn лежит в плоскости NN, нормальной к образующей конуса и проходящей через среднее по длине зуба сечение. Силы в зацеплении: - окруж Ft=2T/dm - радиальн Fr=(Ft tgαwt)cosδ - осев Fa=(Ft tgαwt)sinδ ВИДЫ РАЗРУШЕНИЯ И УСЛОВИЯ ПРОЧНОСТИ ОТКРЫТЫХ И ЗАКРЫТЫХ КОНИЧ. ПЕРЕДАЧ. Все зуб передачи делятся на 2 вида: - открытые - закрытые ОТКРЫТЫЕ. Осн причина разрушения: поломка зуба из-за σизг. Проектирование по условию:σF ≤ [σF]:m→aw→геометрия. Проверочный расчет: σН ≤ [σН] σН-контактная прочность ЗАКРЫТЫЕ.Основная причина разрушения: питтинг-процесс из-за σН. Проектирование по условию: σН ≤ [σН]: aw→m→ геометрия. Проверочный расчет: σF ≤ [σF] - выносливость 7.5. Расчёт зубчатых конических колес на выносливость по контактным напряжениям Площадь поперечного сечения зуба конического колеса и величина удельной силы нормального давления на зуб пропорциональны расстояниям от вершины делительного конуса до рассматриваемого сечения. принято выполнять расчеты по среднему (по ширине зубчатого венца) сечению.
Здесь также, как и в цилиндрических передачах коэффициент Z = ZH · Zm · zε и расчетный момент на шестерне: T1H = T1 · KHα · KHβ · KHv (7.29) Вместе с тем, в отечественной практике большее применение сохранила иная расчётная зависимость [4, с. 184]:
(7.30)
где νH – экспериментальный коэффициент, учитывающий снижение прочности конического колеса в сравнении с цилиндрическим; для прямозубых конических колес νH = 0,85; для кривозубых колёс коэффициент νH назначают в зависимости от твёрдости контактных поверхностей зубьев [4, с. 184].
7.6. Расчет зубьев конических колес на выносливость по напряжениям изгиба
(7.33)
где νF - коэффициент, учитывающий снижение прочности зубьев конического колеса по сравнению с эквивалентным цилиндрическим; для прямозубого конического колеса νF = 0,85; для колеса с круговыми зубьями коэффициент νF назначают в зависимости от твердости материала колеса [4, с. 184]. Следует иметь в виду, что расчету на прочность по напряжениям изгиба подвергают зуб того колеса, для которого соотношение [σF]/YF меньше. Условие равной прочности на изгиб зубьев шестерни и колеса конической передачи:
Если условие (7.34) выполнено, то это означает, что материалы и термическая обработка для шестерни и колеса назначены правильно. Виды разрушения: Поломка зуба. Причина: удар или попадание инородных тел в зону зацепления. Меры предотвращения: защита от инород. тел, повышение поверхност прочности, увелич модуля, ув радиуса, скругление ножки зуба. Питтинг-процесс (устолостное выкрашивание поверхности зуба). Причина: недостаточная поверх прочность. Меры: ув поверх твердости с помощью использования химически неактивных смазок. Зуб шестерни тверже зуба колеса, так как чаще попадает под нагрузку (в передаточное число раз). На поверхности зуба колеса в зоне зацепления образуются микротрещины. При окунании в смазку эти трещины наполняются ей. При повтор попадании под нагрузку масло ув трещины в глубь зуба. В рез-те длит работы на поверхности зуба образ-ся раковины, ямки. Заедание. Меры: повышение поверх твердости, антизадир смазки, модификация зуба (фаски) При выдавливании смазки с контактной поверхности частицы менее тверд зуба привариваются к более тверд зубу. При послед зацеплении эти «лишние» частицы царапают сопряженные зубья в направлении от ножки к вершине зуба. Образивный износ (только для открытых).Меры: повыш поверх твердости. Пластическое течение при перегрузках. Причина:длит работа при перегркзках. Какими достоинствами обладает коническая передача с круговыми зубьями по сравнению с прямозубой? какие модули передачи вам известны? по какому модулю производят расчет на изгиб зубьев конического колеса? Конические передачи менее чувствительны к нарушению точности взаимного расположения колес, их изготовление проще и производится на спец станках для нарезания и шлифования этих колес в усл как массового, так и мелкосерийного производства. Линейная величина в π раз меньшая окружного шага зубьев, наз окружным модулем зубьев mt, а линейная величина, в π раз меньшая нормального шага зубьев, наз нормальным модулем зубьев. Т.о. mt=pt/ π, mn= pn/ π. Для кон зуб колес с прямыми зубьями в качестве стандартного расчетного модуля m зубьев принимают внешний окружной делительный модуль mte. Для кон зуб колес с косыми зубьями в качестве стандартного расчетного модуля зубьев принимают внешний норм делит модуль mne. Расчет на прочность зубьев при изгибе производят по сред значению модуля зубьев m [из др учебника др обозначения]: me – внешний окр модуль; m – средний окр модуль. Внеш окр модуль обыч выбир из станд ряда. Этот модуль наз проииводственным и по его знч-ю опр-ют все геом пар-ры зуб колес (задают размеры зубьев на внеш торце, на кот удобно произв измерения). Сред окр модуль m рассчитывают в завис-ти от внеш окр модуля me. По сред окр модулю производят расчет передачи на прочность при изгибе.
Цилиндрические. Достоинства: Простота изготовления и сборки, нет осевых нагрузок на валы. Плавность хода, коэффициент торцевого перекрытия Недостатки: При V Передаточное число u = z2 / z1 = d2 / d1, где z1, z2 – число зубьев соответственно: шестерни и колеса. Обычно передаточные числа ограничиваются габаритами передачи. В редукторах общего машиностроения максимальные значения передаточных чисел быстроходной ступени U1 = 6,3…8,0; для промежуточной и тихоходной ступеней Umaх = 5,6…6,3 Конические. Достоинства: простота изготовления, монтажа и регулирование по пятну контакта плавность хода, более производителен процесс изготовления, больше нагрузочная способность. Недостатки: очень чувствительны к ошибкам изготовления и монтажа. Передаточное число: 1,50…4,0 Червячные. Достоинства: а) возможность получения большого передаточного отношения; б) плавность и бесшумность работы, возможность точных делительных перемещений; в)возможность передачи между скрещивающимися валами; г) самоторможение; д) высокая кинематическая точность Недостатки: а) низкий КПД; б) необходимость применения для колеса дорогостоящих антифрикционных материалов, что повышает стоимость передачи; в) повышенный износ и склонность к заеданию; г) повышенные требования к точности сборки (точное aw, совпадение главных плоскостей колеса и червяка). Передаточное число: 8…50 Расчеты на прочность Червячные передачи рассчитывают на сопротивление усталости и статическую прочность по контактным напряжениям и напряжениям изгиба. В большинстве случаев напряжения изгиба не определяют размеры передачи и расчет по ним применяют в качестве проверочного. Основное значение имеет расчет на сопротивление контактной усталости, который должен предотвращать в проектируемых передачах выкрашивание, и расчет на заедание. Расчет на износ совмещают с этим расчетом. Расчет на прочность по контактным напряжениям ведут для зацепления в полюсе, что позволяет упростить расчет. σн ≤ | σн |2 выполняют проектный расчет или σн=
После вычисления межосевого расстояния по ГОСТу выбираем Z1,Z2,ms, q, x1 далее следует расчет геометрии и проверочный расчет по σн= Тепловой расчет За счет передачи движения посредствам скольжения, передача может перегреваться, поэтому на завершающем этапе конструирования выполняют тепловой расчет передачи
Если 1. Ребристый корпус (увеличение поверхности теплоотдачи) 2. принудительный обдув корпуса воздухом 3. принудительное охлаждение водой Расчеты червяка Т. к. червяк обязательно проверяют на жесткость, то минимальное значение допускаемого коэффициента запаса прочности [S]=3. Если [S]<3, то: 1. поверхностное упрочнение (обдувка дробью, закалка, ТВЧ, ХТО) 2. изменение конструкции концентратора 3. увеличение диаметра
25.червячная цилиндрическая передача: особенности кинематики, причины нагрева, тепловой расчет и меры, предотвращающие перегрев передачи. Червячная передача состоит из червяка /, т. е. винта с трапецеидальной или близкой к ней по форме резьбой, и червячного колеса 2, т. е. зубчатого колеса с зубьями особой формы, получаемой в результате взаимного огибания с витками червяка Червячные передачи относятся к числу зубчато-ви
|
||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 1140; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.170.38 (0.011 с.) |

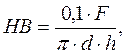
 статические силы – это не изменяющиеся ни по величине, ни по направлению нагрузки (кривая 1) или силы, частота изменения которых во времени на порядок меньше собственной частоты колебаний детали (кривая 2).
статические силы – это не изменяющиеся ни по величине, ни по направлению нагрузки (кривая 1) или силы, частота изменения которых во времени на порядок меньше собственной частоты колебаний детали (кривая 2). =0.
=0.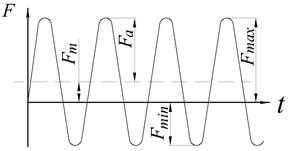
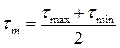
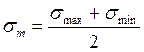
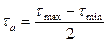
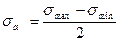

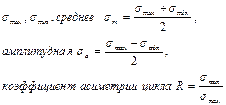
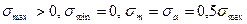
 R=0
R=0
 . По этой причине для косозубых колес принимают
. По этой причине для косозубых колес принимают 

 . Оси колес при этом остаются параллельными. Профиль косого зуба в нормальном сечении совпадает с профилем прямого зуба. В торцевом сечении параметры косого зуба изменяются в зависимости от угла
. Оси колес при этом остаются параллельными. Профиль косого зуба в нормальном сечении совпадает с профилем прямого зуба. В торцевом сечении параметры косого зуба изменяются в зависимости от угла 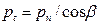

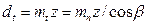
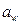

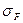

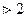 , большая длина зуба—больше нагрузочная способность, больше прочность по
, большая длина зуба—больше нагрузочная способность, больше прочность по 
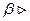 чем косозуб. передачах, то еще больше плавность хода и нагрузочная способность—меньше габариты при одинаковых нагрузках.
чем косозуб. передачах, то еще больше плавность хода и нагрузочная способность—меньше габариты при одинаковых нагрузках.
 необходимо повышать прочность изготовления, иначе возможна большая динамика (опасность удара)
необходимо повышать прочность изготовления, иначе возможна большая динамика (опасность удара)
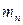 =
=
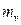


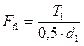
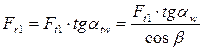
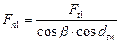 Как видно из рисунка 24г, сила нормального давления на зуб равна Fn = F2 / cosβ.
Как видно из рисунка 24г, сила нормального давления на зуб равна Fn = F2 / cosβ.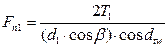
 1. Благодаря наклонному расположению зубьев коэффициент перекрытия εα увеличивается за счёт дополнительной дуги зацепления (Δ = BW · tgβ):
1. Благодаря наклонному расположению зубьев коэффициент перекрытия εα увеличивается за счёт дополнительной дуги зацепления (Δ = BW · tgβ):
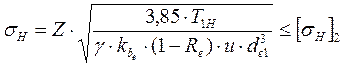

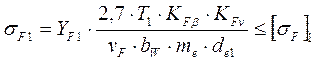
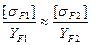 (7.34)
(7.34) необходимо повышать прочность изготовления, иначе возможна большая динамика (опасность удара). Из-за наклона зуба появляется осевая нагрузка на вал и в зацеплении.
необходимо повышать прочность изготовления, иначе возможна большая динамика (опасность удара). Из-за наклона зуба появляется осевая нагрузка на вал и в зацеплении.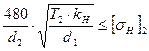 проверочный расчет
проверочный расчет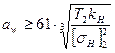 , мм, где Т - крутящий момент;Нмм. kH – коэффициент запаса прочности по контактным напряжениям;
, мм, где Т - крутящий момент;Нмм. kH – коэффициент запаса прочности по контактным напряжениям; и
и 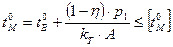 где tВ=200С, р – мощность, ɳ - КПД, А – площадь теплоотдающей поверхности мм3
где tВ=200С, р – мощность, ɳ - КПД, А – площадь теплоотдающей поверхности мм3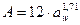 , kт – коэффициент теплоотдачи, kт=17…40,
, kт – коэффициент теплоотдачи, kт=17…40,  = 900С…950С зависит от марки масла
= 900С…950С зависит от марки масла то:
то:


