
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Робота термодинамічних процесівСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Нехай розширюючись в циліндрі, газ переміщує поршень на віддаль
Тут Робота розширення газу в циліндрі матиме знак „+”, адже в цьому випадку напрям діячої сили співпадає з напрямом руху поршня. Елементарну роботу розширення газу можна виразити через нескінченно малу зміну об’єму. Якщо
Якщо в процесі виконання роботи початковий об’єм був
1) процес протікає при незмінному об’ємі (ізохорний процес,
2) процес здійснюється при постійному тиску (ізобарний процес,
Зауваження: Домовимося позначати об’єм одного моля газу при заданих умовах ( Оборотне ізотермічне розширення газу ( Для ідеального газу
При ізотермічному переході системи із стану (1) до стану (2) виконана робота дорівнює:
Максимальну роботу, що виконується при оборотному ізотермічному розширенні можна записати через тиски:
Враховуючи, що тиск пропорційний концентрації атомів
Теплоємність Середню питому (с) або мольну теплоємність (С) можна визначити експериментально як відношення кількості теплоти
Щоб знайти істинні значення теплоємностей, необхідною умовою є
При низьких температурах (нижче 15К) теплоємність можна пояснити лише з позицій квантової теорії. У спрощеній формі ця теорія дає такий вираз для низькотемпературної теплоємності:
ТЕПЛОВІ ЕФЕКТИ ХІМІЧНИХ РЕАКЦІЙ. Ентальпія Запишемо перший закон термодинаміки для процесу в якому виконується лише ізобарична робота розширення
Якщо
або згрупувавши за станами системи, одержимо значення
Висновок: теплота, що передається в ізобаричному процесі, дорівнює приросту ентальпії Якщо реакції протікають без участі газової фази, то для рідин і твердих тіл зміна об’єму з температурою є незначною Розглянемо термохімічний процес з участю газової фази при
або
де
Для ідеального газу
Властивості ентальпії враховує закон Гесса: якщо термодинамічний процес складається з декількох етапів, то загальний тепловий ефект цього процесу дорівнює алгебраїчній сумі теплових ефектів всіх етапів. Покажемо це. Нехай поцес складається із
ЦИКЛ КАРНО В теплових машинах деяка кількість речовини, що називається робочим тілом, здійснює циклічну послідовність процесів і перетворює теплоту в роботу, періодично повертаючись до початкового стану. Цикл Карно – оборотний цикл, який складається з чотирьох процесів: двох ізотермічних і двох адіабатних. Робочим тілом є ідеальний газ. Можна показати, що коефіцієнт корисної дії теплової машини можна виразити через температури нагрівника
З іншого боку, к.к.д. можна виразити через відібрану від нагрівника теплоту
Другий закон термодинаміки Перший закон термодинаміки стверджує, що при перетворенні однієї форми енергії в іншу повна енергія зберігається, але не вказує ніяких інших обмежень відносно процесів перетворень. Другий закон термодинаміки дає можливість розрахувати, яка ж частина теплоти може бути перетворена в роботу при циклічному процесі, та вказати, чи є даний процес самочинним чи ні. Самочинними (або позитивними) називають такі процеси, які протікають самі по собі, без зовнішнього впливу в напрямку досягнення термодинамічною системою рівноваги. Якщо процеси здійснюються під дією зовнішнього впливу в напрямку віддалення системи від стану рівноваги, то їх називають не самочинними, або негативними. В ізольованій системі виключаються всілякі зовнішні впливи, тому в ній можуть протікати лише самочинні процеси. Передбачати напрямок процесу дає можливість другий закон термодинаміки: Єдиним результатом будь-якої сукупності процесів не може бути перехід теплоти від менш нагрітого тіла до більш нагрітого (постулат Клаузіуса). Процеси теплопровідності є незворотними. Єдиним результатом будь-якої сукупності процесів не може бути перетворення теплоти в роботу, тобто не можна створити вічний двигун другого роду (постулат Томсона). Перший закон термодинаміки заперечує можливість створення машини, яка творила б енергію з нічого. Другий закон термодинаміки заперечує можливість створення такої машини, яка змогла б перетворювати теплоту навколишнього середовища в роботу лише за рахунок охолодження навколишнього середовища. Ентропія Відомо, що для оборотного циклу Карно ККД може бути записаний через взяту у нагрівника теплоту Q 1 та прийняту холодильником теплоту Q 2, або через їх температури, відповідно T 1 і T 2.
Прирівняємо праві частини цих виразів:
Відношення
Обчислення ентропії Для обчислення ентропії ідеального газу застосуємо перший закон термодинаміки в диференціальній формі: Розділивши на
Інтегруючи вираз, знаходимо зміну ентропії в термодинамічному процесі:
Підставивши межі інтегрування можна записати:
Якщо Очевидно, що для n молів відповідні зміни ентропії будуть в n разів більшими. 1. Мольна ентропія речовини змінюється за рахунок зміни температури. При збільшенні температури (при нагріванні) ентропія зростає і навпаки. 2. Ентропія зростає при зростанні об`єму газу. 3. Ріст ентропії характеризує зменшення порядку в термодинамічній системі. При збільшенні температури посилюється тепловий рух, а при збільшенні об`єму зменшується ймовірність того, що в заданому елементарному об`ємові Δnвдасться знайти молекулу. Сказане яскраво демонструється зміною ентропії при фазових переходах першого роду (випаровування і плавлення). Ці процеси є ізотермічними (Т = const). Зміна ентропії ізотермічного процесу буде:
Ентропія суміші газів Якщо сполучити два резервуари з різними газами, то гази почнуть дифундувати з одного об’єму до іншого навіть тоді, коли тиск і температура в обох резервуарах будуть однаковими. Якщо гази ідеальні, то компоненти системи (гази) вестимуть себе незалежно один від іншого. При ізотермічно – ізобарному процесі зміна ентропії дорівнює сумі таких змін для кожного газу при його розширенні до об`єму v, тобто, ентропія є величиною екстенсивною:
де
З одержаного рівняння видно, що зміна ентропії при змішуванні завжди позитивна Наприклад, змішується два молі азоту і один водню при однакових для обох газів початкових умовах. Запишемо:
Постулат Планка. Абсолютні значення ентропії Ентропія індивідуальної кристалічної речовини при абсолютному нулю дорівнює нулю: Цей постулат справедливий лише для ідеальних кристалів, тобто, таких, у яких немає ніяких дефектів. Якщо у кристалі присутні дефекти, то вони будуть збільшувати його ентропію, адже дефекти – це будь які порушення порядку. При температурі T для ідеального кристалу можна обчислити абсолютне значення ентропії:
Слід нагадати, що Постулат Планка використовується для обчислення абсолютних значень ентропій хімічних сполук. Це важливо при розрахунку хімічних рівноваг. Рівняння для обчислення абсолютної ентропії газу при деякій температурі
|
||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 487; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.227.209.89 (0.01 с.) |

 , а із зовні на цей поршень діє тиск
, а із зовні на цей поршень діє тиск 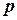 . Сила тиску
. Сила тиску  залежить від площі поверхні поршня:
залежить від площі поверхні поршня:  . Робота сили
. Робота сили 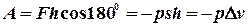 .
. - зміна об’єму газу під поршнем.
- зміна об’єму газу під поршнем. , то
, то  і елементарна робота розширення запишеться так:
і елементарна робота розширення запишеться так: .
.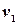 , а кінцевий
, а кінцевий  , то виконана робота визначиться шляхом інтегрування:
, то виконана робота визначиться шляхом інтегрування: , наприклад:
, наприклад: ):
): ;
; ):
): .
. ) буквою
) буквою  , а об’єм
, а об’єм  молів газу – буквою
молів газу – буквою  . Отже, за однакових умов:
. Отже, за однакових умов:  .
.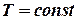 ).
). , звідки
, звідки ; тут
; тут 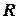 ,
,  є константи.
є константи. ;
; .
.

 , одержимо:
, одержимо: .
.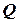 , що поглинається при нагріванні відповідно 1кілограму або 1 моля речовини на
, що поглинається при нагріванні відповідно 1кілограму або 1 моля речовини на 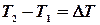 градусів при заданих умовах. Розрізняють теплоємність при сталому тиску
градусів при заданих умовах. Розрізняють теплоємність при сталому тиску 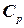 або сталому об’ємі
або сталому об’ємі  . Середня теплоємність
. Середня теплоємність  в температурному інтервалі
в температурному інтервалі 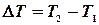 визначається відношенням переданого тепла
визначається відношенням переданого тепла  :
: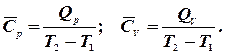
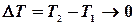 , тобто,
, тобто, 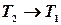 :
: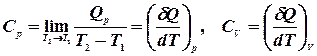 .
.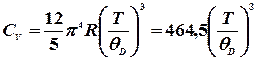 (формула Дебая)
(формула Дебая)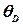 – температура Дебая. Вона знаходиться емпірично для кожної речовини і дається в довідниках.
– температура Дебая. Вона знаходиться емпірично для кожної речовини і дається в довідниках.
 ;
; .
. , де
, де 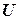 - функція стану термодинамічної системи. Отже, сума
- функція стану термодинамічної системи. Отже, сума 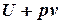 теж є функцією стану і її зміна не залежить від шляху перебігу процесу, а лише залежить від початкового та кінцевого станів термодинамічної системи. Цю функцію називають ентальпією
теж є функцією стану і її зміна не залежить від шляху перебігу процесу, а лише залежить від початкового та кінцевого станів термодинамічної системи. Цю функцію називають ентальпією  . Якщо система переходить від стану (1) до стану (2), то після інтегрування виразу
. Якщо система переходить від стану (1) до стану (2), то після інтегрування виразу  знайдемо:
знайдемо: ,
,  ,
, :
: ,
, . Абсолютне значення ентальпії
. Абсолютне значення ентальпії  не можна обчислити за допомогою рівнянь термодинаміки тому, що до нього входить абсолютна величина внутрішньої енергії
не можна обчислити за допомогою рівнянь термодинаміки тому, що до нього входить абсолютна величина внутрішньої енергії  і цією величиною можна знехтувати. Тоді
і цією величиною можна знехтувати. Тоді 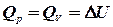 .
. для ідеального газу, що переходить із початкового стану (1) до кінцевого (2).
для ідеального газу, що переходить із початкового стану (1) до кінцевого (2). ,
, ,
, ‑ зміна числа молів газоподібних речовин в процесі реакції. Враховуючи, що
‑ зміна числа молів газоподібних речовин в процесі реакції. Враховуючи, що  де
де  , знайдемо передану теплоту при сталому тиску:
, знайдемо передану теплоту при сталому тиску:
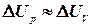 . Виходячи з цього, одержимо формулу для обчислення зміни ентальпії ідеального газу в ізобаричному та ізотермічному процесах:
. Виходячи з цього, одержимо формулу для обчислення зміни ентальпії ідеального газу в ізобаричному та ізотермічному процесах:
 .
. етапів. Для
етапів. Для 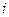 - го етапу
- го етапу  . Знаходимо суму ентальпій всіх етапів:
. Знаходимо суму ентальпій всіх етапів:
 і холодильника
і холодильника  . Чим більша різниця температур, тим вищий к.к.д.
. Чим більша різниця температур, тим вищий к.к.д. .
.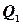 і теплоту, прийняту холодильником
і теплоту, прийняту холодильником  : чим більша різниця цих теплот, тим вищий к.к.д..
: чим більша різниця цих теплот, тим вищий к.к.д..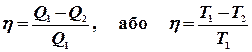

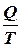 називають приведеною теплотою. Різниця приведених теплот нагрівника і холодильника дорівнює нулю. Це справедливо і для нескінченно малого оборотного циклу Карно:
називають приведеною теплотою. Різниця приведених теплот нагрівника і холодильника дорівнює нулю. Це справедливо і для нескінченно малого оборотного циклу Карно: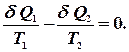
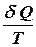 називається елементарною приведеною теплотою для нескінченно малого циклу. Вона дорівнює повному диференціалу від ентропії (від грецького troph - перетворення).
називається елементарною приведеною теплотою для нескінченно малого циклу. Вона дорівнює повному диференціалу від ентропії (від грецького troph - перетворення).
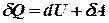 , або
, або 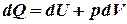 . Введемо заміни:
. Введемо заміни: 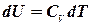 ;
; 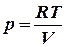 ;
; 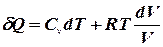 .
.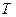 одержимо диференціал ентропії:
одержимо диференціал ентропії:

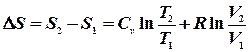
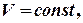 то
то 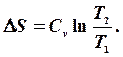 Якщо
Якщо  то
то 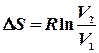 .
.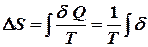
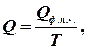
 - це мольна теплота (ентальпія) фазового переходу першого роду (прихована теплота плавлення або випаровування), якщо система приймає тепло, то ентропія зростає. Отже, при плавленні збільшується безпорядок в системі. Зникає далекий порядок, залишається лише ближній, у рідині утворюються мікропустоти (до 3% від її об`єму). Зростає тепловий рух. Те ж саме відбувається і при випаровуванні. Порядок зменшується. Зникає ближній порядок, атоми і молекули переходять у газову фазу, де ймовірність їх знайти в заданому елементарному об’ємі зменшується при збільшенні об`єму. Отже, ентропія – це міра безпорядку.
- це мольна теплота (ентальпія) фазового переходу першого роду (прихована теплота плавлення або випаровування), якщо система приймає тепло, то ентропія зростає. Отже, при плавленні збільшується безпорядок в системі. Зникає далекий порядок, залишається лише ближній, у рідині утворюються мікропустоти (до 3% від її об`єму). Зростає тепловий рух. Те ж саме відбувається і при випаровуванні. Порядок зменшується. Зникає ближній порядок, атоми і молекули переходять у газову фазу, де ймовірність їх знайти в заданому елементарному об’ємі зменшується при збільшенні об`єму. Отже, ентропія – це міра безпорядку.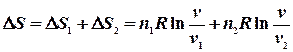 ,
, кількості молів кожного газу при температурі
кількості молів кожного газу при температурі 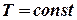 і спільному тиску
і спільному тиску 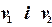 до об`єму суміші
до об`єму суміші  .
.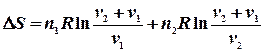 .
.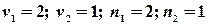


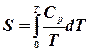 .
.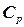 змінюється пропорційно T 3
змінюється пропорційно T 3  , отже,
, отже, 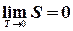 . В принципі абсолютний нуль досягти неможливо. Залишаються нульові коливання.
. В принципі абсолютний нуль досягти неможливо. Залишаються нульові коливання.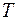 має вид:
має вид:



