Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Характеристичні функції у термодинаміціСодержание книги Поиск на нашем сайте Застосуємо перший закон термодинаміки до рівноважних і не рівноважних процесів. Нагадаємо, що
де знак рівності стосується рівноважних процесів, а нерівності – неврівноважених. Віднімемо від обох частин цього виразу
де Для рівноважного процесу елементарна робота є повним диференціалом і її можна виразити через ентропію:
Отже, робота рівноважного процесу завжди буде більшою, ніж не рівноважного:
Робота рівноважного процесу є максимальною. Вона не залежить від шляху і визначається початковим і кінцевим станами системи. Далі розглядатимемо лише рівноважні процеси. Виділимо із повної елементарної роботи ту її частину, що відповідає роботі розширення pdv (робота сили тиску) dA=dA* + pdv. Тепер можна записати: dU=TdS - dA*- pdv, звідки dA* =TdS - dU – pdv Ізохорно - ізотермічний потенціал. Нехай
Вираз в дужках позначимо буквою F. Це функція стану, що називається ізохорно - ізотермічним потенціалом або вільною енергією Гельмгольца. Отже,
Проінтегруємо вираз
Ізохорно – ізотермічний потенціал не залежить від способу переходу системи від стану (1) до стану (2). робота при ізохорно - ізотермічних рівноважних процесах дорівнює взятій із знаком “‑” зміні вільної енергії системи. Внутрішню енергію системи можна розглядати як таку, що складається із двох частин - вільної енергії
Остання не може бути перетвореною в роботу і лише переходить в теплоту:
Ентропія є фактором ємності зв’язаної енергії в ізохорно – ізотермічному процесі. Обчислимо повний диференціал від ізохорно – ізотермічного потенціалу:
Якщо виконується лише робота розширення, то
звідки для
Якщо
Ізобарно-ізотермічний потенціал ( Запишемо для цих умов елементарну роботу і винесемо за дужки знак “‑” і знак диференціалу:
Введемо позначення:
Нову термодинамічну функцію Знайдемо повний диференціал від термодинамічного потенціалу, вважаючи, що всі величини є змінними:
Підставивши у цей вираз значення
Враховуючи, що
За умов встановлення термодинамічної рівноваги потенціали Хімічний потенціал До цього часу ми розглядали закриті системи, тобто такі, які не можуть обмінюватися із зовнішнім середовищем речовиною, але обмінюється енергією. Тепер розглянемо відкриту систему, в якій маси різних компонентів
Знайдемо повний диференціал внутрішньої енергії для відкритої термодинамічної системи:
Розглянемо перший закон термодинаміки для закритої системи, яка не обмінюється речовиною з навколишнім середовищем:
де
або, враховуючи, що для такої системи U = U(S,v), знайдемо:
Порівнюючи два вирази, одержимо:
Коефіцієнт при
тут
Хімічний потенціал є інтенсивною величиною, яка характеризує дану фазу подібно до тиску та температури. Наприклад, різниця хімічних потенціалів у двох фазах визначає напрям, в якому буде відбуватися самочинна дифузія речовини аналогічно тому, як різниця температур визначає напрям потоку тепла.
|
||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 442; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.008 с.) |

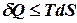 ,
, і одержимо зліва елементарну роботу:
і одержимо зліва елементарну роботу: , або
, або 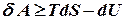 ,
,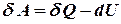 .
.
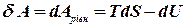 .
. Для не рівноважного процесу
Для не рівноважного процесу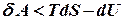 .
.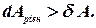
 (електричними, хімічними, магнітними, силами поверхневого натягу і т. д.):
(електричними, хімічними, магнітними, силами поверхневого натягу і т. д.):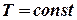 , v = const, тоді dv = 0. Запишемо для цих умов елементарну роботу і винесемо за дужки знак “‑” і знак диференціалу:
, v = const, тоді dv = 0. Запишемо для цих умов елементарну роботу і винесемо за дужки знак “‑” і знак диференціалу: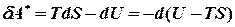 .
.  .
.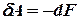 :
: ;
;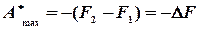 .
. і зв’язаної
і зв’язаної 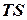 :
:
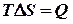 .
.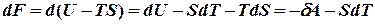 .
. ,
,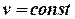 можна записати:
можна записати: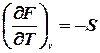 .
.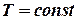 , то одержимо:
, то одержимо: .
. )
)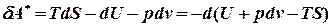 .
. , або
, або 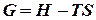 .
.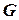 називають ізобарно-ізотермічним потенціалом, або ізобарним потенціалом, або вільною енергією при сталому тиску, або термодинамічним потенціалом.
називають ізобарно-ізотермічним потенціалом, або ізобарним потенціалом, або вільною енергією при сталому тиску, або термодинамічним потенціалом.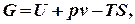
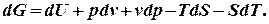
 одержимо:
одержимо: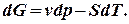
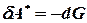 , після інтегрування одержимо:
, після інтегрування одержимо:
 або відповідна кількість їх молів
або відповідна кількість їх молів  можуть довільно змінюватися. Це означає, що внутрішня енергія системи при
можуть довільно змінюватися. Це означає, що внутрішня енергія системи при 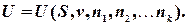
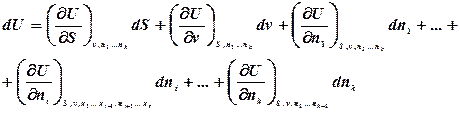
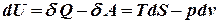

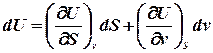
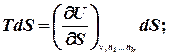
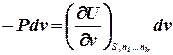
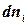 називають хімічним потенціалом.
називають хімічним потенціалом.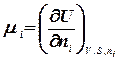
 означає всі речовини, крім і – тої. Приріст будь-якої термодинамічної функції при зміні маси даної речовини за умови незмінності всіх інших параметрів системи, називається хімічним потенціалом.
означає всі речовини, крім і – тої. Приріст будь-якої термодинамічної функції при зміні маси даної речовини за умови незмінності всіх інших параметрів системи, називається хімічним потенціалом.