
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Швидкість, це фізична величина , що показує, як змінюється переміщення матеріальної точки за одиницю часу.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Прискорення Прискоренням називається фiзична величина, що характеризує змiну швидкостi з часом. Розрiзняють прискорення середнє i миттєве. Середнє прискорення (
Напрямок вектора Миттєве прискорення (або просто прискорення)
Використовуючи рівність (1.16) маємо,
Прискорення є векторна величина, що дорівнює похiднiй вектора швидкості за часом. З урахуванням формули (1.16) прискорення можна записати як другу похiдну радіус-вектора за часом:
Повне прискорення дорівнює їх векторнiй сумi
Для знаходження цих складових прискорення, пiдставимо вираз для швидкостi в означення (1.18) i зробимо вiдповiдне диференцiювання:
Враховуючи, що
Матимемо вираз:
Можна показати, що
де Остаточно вираз (1.21) набуде вигляду:
Порiвнюючи цей вираз з рiвнянням (1.20) бачимо, що перший член виразу визначає тангенцiальне прискорення
що спрямоване по дотичнiй до траєкторiї в данiй точцi i за модулем дорівнює
Другий член визначає нормальне прискорення
що спрямоване по нормалi до траєкторії в данiй точцi (тобто до центру кривизни траєкторiї) i за модулем дорівнює
Як видно з рис.1.9, модуль повного прискорення
Цi проекцiї знаходяться як похiднi за часом:
Обернена задача кiнематики Обернена задача кiнематики полягає в знаходженнi рiвняння руху за вiдомими характеристиками руху. Розглянемо, як за вiдомими
Щоб знайти весь шлях, пройдений за певний промiжок часу
Графiчно цей iнтеграл зображений на рис. 1.10, з якого видно, що шлях чисельно дорiвнює площi фiгури (криволiнiйної трапеції), що обмежена кривою Аналогiчно за вiдомим прискоренням можна знайти швидкiсть у довiльний момент часу
Якщо в початковий момент часу
Застосуємо наведенi вирази для рiвнозмiнного прямолiнiйного руху при
З виразу (1.33) можна одержати:
Остаточно:
Знайшовши
Рух матерiальної точки по колу Пiд час розглядання руху матерiальної точки по колу крім характеристик Кут повороту Положення матерiальної точки пiд час руху по колу можна визначити кутом повороту
Із геометрiї вiдомий зв’язок мiж довжиною дуги та кутом повороту:
де R— радiус кола. Для малих промiжкiв часу
де Кутова швидкiсть Аналогiчно до означень, наведених в п. 1.3.2, розрiзняють середню і миттєву кутові швидкостi. Середня кутова швидкiсть (
Для миттєвої кутової швидкостi (або просто кутової швидкості) можна записати:
тобто чисельно вона дорiвнює похiднiй кута повороту за часом. Вимiрюється кутова швидкiсть у радiанах за секунду (рад/с). Вона теж є псевдовектором, що напрямлений вздовж осi обертання, вiдповiдно до правила гвинта (рис. 1.11). Тому можна записати у векторному виглядi:
Якщо з часом кутова швидкiсть не змiнюється, тобто
У цьому разі
звідки
Величина, обернена до перiоду, називається частотою обертання
Вона показує, скiльки обертiв по колу робить точка за одиницю часу i вимiрюється в секунду мінус першій ступені (с-1) або в герцах (Гц). Зв’язок мiж частотою i кутовою частотою має такий вигляд:
Кутове прискорення Кутове прискорення характеризує змiну кутової швидкостi за часом. Аналогiчно до означень, наведених в п. 1.3.3, розрiзняють середнє i миттєве кутове прискорення. Середнє кутове прискорення (
Для миттєвого кутового прискорення (або просто кутового прискорення)
Тобто воно чисельно дорiвнює першiй похiднiй кутової швидкості за часом або другiй похiднiй кута повороту за часом. Вимiрюється кутове прискорення в радiанах на секунду в квадратi (рад/с2). Воно також є псевдовектором, спрямованим по осi обертання
На рис.1.11, в напрямок Знайдемо зв’язок мiж лiнiйними i кутовими характеристиками руху. 1. Зв’язок мiж лiнiйною i кутовою швидкiстю:
тобто
2. Зв’язок мiж тангенцiальним i кутовим прискоренням:
тобто
3. Зв’язок між нормальним прискоренням і кутовою швидкістю:
тобто
Для розв’язання оберненої задачi під час руху точки по колу використовують вирази аналогiчнi виразам (1.33) та (1.35):
Тодi для рiвнозмiнного руху по колу вiдповiднi математичнi перетворення дадуть вирази аналогiчнi виразам (1.36), (1.37),(1.38):
де
|
||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 408; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.141.155 (0.007 с.) |

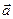 )— це векторна величина, що визначається вiдношенням змiни швидкостi
)— це векторна величина, що визначається вiдношенням змiни швидкостi 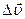 до промiжку часу
до промiжку часу 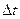 , за який ця змiна вiдбулася:
, за який ця змiна вiдбулася: (1.16)
(1.16)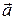 збігається з напрямком
збігається з напрямком  , тобто прискорення в певний момент часу це границя, до якої прямує середнє прискорення при
, тобто прискорення в певний момент часу це границя, до якої прямує середнє прискорення при 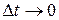
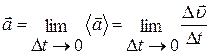 (1.17)
(1.17) (1.18)
(1.18) (1.19)
(1.19)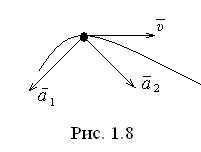 Як буде показано далi, в загалом вектор
Як буде показано далi, в загалом вектор  в бiк угнутостi траєкторiї. На рис. 1.8. вектор
в бiк угнутостi траєкторiї. На рис. 1.8. вектор  вiдповідає прискореному руху, вектор
вiдповідає прискореному руху, вектор  —сповiльненому руху. Оскiльки змiна швидкостi вiдбувається i за модулем i за на напрямком, розрiзняють двi складовi прискорення:
—сповiльненому руху. Оскiльки змiна швидкостi вiдбувається i за модулем i за на напрямком, розрiзняють двi складовi прискорення: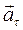 - прискорення (дотичне), яке характеризує змiну швидкості за модулем i спрямоване по дотичнiй до траєкторії;
- прискорення (дотичне), яке характеризує змiну швидкості за модулем i спрямоване по дотичнiй до траєкторії;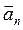 - нормальне прискорення (доцентрове), яке характеризує змiну швидкості за напрямком i спрямоване по нормалi до траєкторії.
- нормальне прискорення (доцентрове), яке характеризує змiну швидкості за напрямком i спрямоване по нормалi до траєкторії. (1.20)
(1.20)

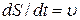 , а
, а  можна подати у виглядi:
можна подати у виглядi:
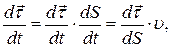
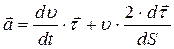 (1.21)
(1.21) , (1.22)
, (1.22)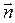 - орт нормалі, R – радіус кривизни траєкторії в даній точці.
- орт нормалі, R – радіус кривизни траєкторії в даній точці. (1.23)
(1.23) (1.24)
(1.24)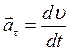 .
. 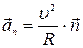 , (1.26)
, (1.26)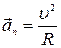 (1.27)
(1.27)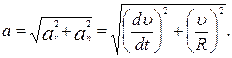 (1.28)
(1.28) Аналогiчно до того, як записувався вектор швидкостi, вектор прискорення теж можна подати через проекцiї
Аналогiчно до того, як записувався вектор швидкостi, вектор прискорення теж можна подати через проекцiї 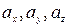 на координатнi осi:
на координатнi осi: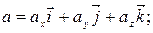 (1.29)
(1.29) (1.30)
(1.30)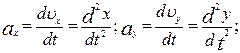
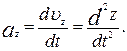 (1.31)
(1.31)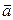 можна знайти рiвняння руху в траєкторному виглядi
можна знайти рiвняння руху в траєкторному виглядi 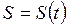 . Запишемо з виразу (1.12) елементарний шлях, пройдений за час
. Запишемо з виразу (1.12) елементарний шлях, пройдений за час 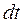 :
: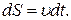 (1.32)
(1.32) , слід проiнтегрувати цей вираз:
, слід проiнтегрувати цей вираз: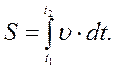 (1.33)
(1.33)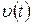 .
.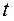 :
: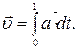 (1.34)
(1.34) , тiло мало початкову швидкiсть
, тiло мало початкову швидкiсть  , то
, то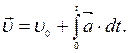 (1.35)
(1.35)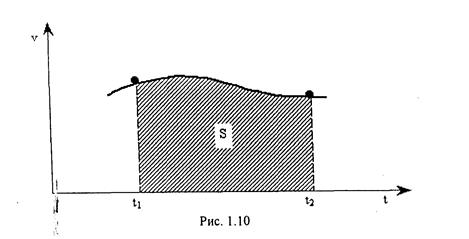
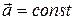 . Тодi рiвняння (1.35) перепишеться:
. Тодi рiвняння (1.35) перепишеться: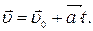 (1.36)
(1.36)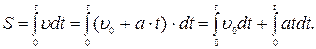
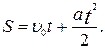 (1.37)
(1.37)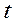 з виразу (1.36) i пiдставивши його у вираз (1.37), можна одержати рiвняння, яке часто зручно використовувати в задачах:
з виразу (1.36) i пiдставивши його у вираз (1.37), можна одержати рiвняння, яке часто зручно використовувати в задачах: (1.38)
(1.38) , якi в даному разi називаються лiнiйними, зручно користуватися так званими кутовими характеристиками руху: кутом повороту, кутовою швидкiстю, кутовим прискоренням.
, якi в даному разi називаються лiнiйними, зручно користуватися так званими кутовими характеристиками руху: кутом повороту, кутовою швидкiстю, кутовим прискоренням. . Як видно з рис. 1.11,а, кут повороту з центральним кутом, який вiдповiдає дузi
. Як видно з рис. 1.11,а, кут повороту з центральним кутом, який вiдповiдає дузi 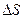 , описанiй матерiальною точкою за час
, описанiй матерiальною точкою за час 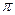 , а при N обертах:
, а при N обертах: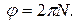 (1.39)
(1.39) (1.40)
(1.40)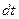 цей вираз матиме вигляд:
цей вираз матиме вигляд: (1.41)
(1.41) - елементарний кут повороту. Для того, щоб показати i напрямок руху точки по колу, домовились елементарний кут повороту показувати як вектор
- елементарний кут повороту. Для того, щоб показати i напрямок руху точки по колу, домовились елементарний кут повороту показувати як вектор  ) визначається вiдношенням кута повороту
) визначається вiдношенням кута повороту  (1.42)
(1.42)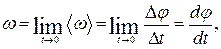 (1.43)
(1.43) (1.44)
(1.44)
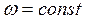 , рух по колу називається рiвномiрним, для нього
, рух по колу називається рiвномiрним, для нього (1. 45)
(1. 45)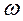 називають циклічною частотою обертання. Час, за який матерiальна точка проходить один оберт по колу, називається перiодом обертання Т, який вимiрюється в секундах. Вираз (1.45) дає:
називають циклічною частотою обертання. Час, за який матерiальна точка проходить один оберт по колу, називається перiодом обертання Т, який вимiрюється в секундах. Вираз (1.45) дає: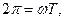 (1.46)
(1.46)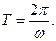
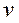 :
: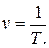 (1.47)
(1.47)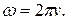 (1.48)
(1.48) ) визначається вiдношенням змiни кутової швидкостi до вiдповiдного промiжку часу:
) визначається вiдношенням змiни кутової швидкостi до вiдповiдного промiжку часу: (1.49)
(1.49) можна записати:
можна записати: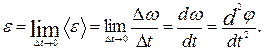 (1.50)
(1.50)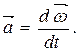 (1.51)
(1.51)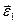 вiдповiдає прискореному руху по колу, напрямок
вiдповiдає прискореному руху по колу, напрямок 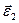 — сповiльненому руху по колу.
— сповiльненому руху по колу.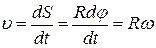
 (1.52)
(1.52)
 (1.53)
(1.53)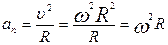
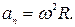 (1.54)
(1.54)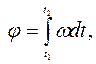 (1.55)
(1.55) (1. 56)
(1. 56)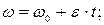 (1.57)
(1.57)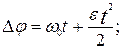 (1.58)
(1.58)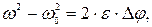 (1.59)
(1.59) — початкова кутова швидкiсть у момент часу t =0,
— початкова кутова швидкiсть у момент часу t =0, 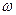 — кутова швидкiсть у момент часу t.
— кутова швидкiсть у момент часу t.


