
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Неiнерцiальнi системи вiдлiкуСодержание книги
Поиск на нашем сайте
Досi ми розглядали рух в iнерцiальних системах вiдлiку. У таких системах, як вiдомо, виконується другий закон Ньютона, який можна записати у виглядi
Розглянемо тепер неiнерцiальнi системи вiдлiку, тобто такi, що рухаються прискорено вiдносно iнерцiальних систем. Нехай неiнерцiальна система К¢ рухається вздовж осi О х iнерцiальної системи К (рис. 2.15). Тодi для координати х ¢ точки М можна записати:
Продиференцiюємо цей вираз двiчi за часом
де Отже,
Помножимо лiву i праву частину цього виразу на масу точки m:
Бачимо, що в iнерцiальнiй системi в другому законi Ньютона крiм “звичайної” сили F з’явилася додаткова сила -
тобто сила iнерції напрямлена протилежно до прискорення неiнерцiальної системи вiдносно iнерцiальної. Сили iнерцiї можна виміряти. Наприклад, прилади, що вимiрюють сили інерції, дають змогу з великою точнiстю визначати мiсце перебування лiтака чи ракети. Оскільки сили iнерцiї зумовленi прискореним рухом неiнерцiальної системи вiдлiку, вони можуть проявлятися не тiльки при поступальному, але й при обертальному русi. Сили iнерцii в системах, що обертаються Нехай маємо диск радiуса R, що обертається навколо нерухомої осi з постiйною кутовою швидкістю w. Зв’яжемо з вiссю iнерцiальну систему К, що не рухається, тодi диск буде неiнерцiальною системою К¢, що обертається. Розглянемо кульку на нитцi, що лежить нерухомо на краю диска (рис. 2.16). Маса кульки m. В системi К на неї дiє сила натягу
У системi К’, в якiй кулька є нерухомою, крiм сили
Ця сила завжди перпендикулярна осi обертання i спрямована по радiусу вiд центра кола. Вiдцентрова сила iнерцiї виникає в усiх системах вiдлiку, що обертаються, i не залежить вiд того, нерухоме тiло в цiй системi, чи рухається. Така сила, наприклад, дiє на нерухоме тiло в зв’язку з обертанням Землi (рис.2.17).
У положенні 2 на екваторi сила тяжiння за модулем дорiвнюватиме рiзницi:
У положеннi 3 на полюсi Саме тому на полюсi прискорення вiльного падiння найбiльше (9,83 м/с), а на екваторi — найменше (9,78 м/с). Загалом вираз для вiдцентрової сили є таким:
де r - радiус-вектор матерiальної точки. Якщо тiло рухається в неiнерцiальнiй системi, що обертається, то крiм вiдцентрової сили виникає ще одна сила iнерцiї, що називається силою Корiолiса Fк. Нехай кулька, що розглянута на рис 2.16, рухається рiвномiрно по краю диска зi швидкiстю υ вiдносно диска, тобто системи К¢ (рис. 2.18). Лiнiйна швидкiсть точок краю диска в системi К дорiвнює
Тодi її доцентрове прискорення вiдносно системи К. буде:
Помножимо лiвi й правi частини на m:
де Тоді для системи К можна записати:
тобто К¢ “звичайної” сили F нат на кульку дiють: вiдцентрова сила Оскiльки для нашого прикладу кут мiж векторами wі υ дорiвнює
Звернімо увагу, що оскiльки сила Корiолiса перпендикулярна до вектора швидкості υ, вона не змінює чисельного значення швидкостi, а змiнює лише її напрямок, тобто викривляє траєкторiю. В умовах Землi, наприклад, це приводить до того, що рiки північної пiвкулi пiдмивають саме правi береги. Слiд зазначити, що введення сил iнерцiї не є вкрай необхiдним. У принципi будь-який рух можна розглянути, наприклад, в гелiоцентричнiй, тобто iнерцiальнiй, системi вiдлiку. Але на практицi здебільшого (особливо в авiацiї), розглядають рух вiдносно неiнерцiальної системи, якою є Земля, виявляється набагато зручнішим i простішим.
ЗАКОНИ ЗБЕРЕЖЕННЯ Найбiльш фундаментальними законами природи у фiзицi є закони збереження. В цих законах йдеться про те, що в замкнутiй (iзольованій) системi за будь-яких фiзичних процесів певнi фiзичнi величини завжди залишаються постiйними, тобто не змiнюються з часом. Закони збереження можуть бути загальними та частковими. Загальнi закони збереження вiрнi для всiх фiзичних явищ, а часткові — тiльки для деяких. Так, закони збереження енергiї iмпульсу, моменту iмпульсу виконуються в усiх фiзичних явищах, вони є загальними законами, а закон збереження механiчної енергiї виконується тiльки в механiчних процесах, вiн є частковим законом. Нагадаємо, що в механiчнiй системi можуть дiяти внутрiшнi i зовнiшнi сили. Система, на яку зовнiшнi сили не діють, називається замкненою системою. Зрозумiло, що в земних умовах замкнених систем немає хоча б тому, що завжди дiють сили тяжiння. Проте реальну систему можна вважати замкненою, якщо внутрiшнi сили взаємодiї набагато бiльші зовнiшнiх сил або рiвнодiйна зовнiшнiх сил дорiвнює нулю.
|
|||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 280; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.12.181 (0.009 с.) |

 (2.72)
(2.72)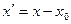 (2.73)
(2.73)
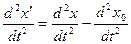 , (2.74)
, (2.74) - прискорення точки в системі К,
- прискорення точки в системі К, 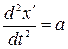 - прискорення точки в системі К¢,
- прискорення точки в системі К¢, 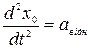 - прискорення системи К відносно системи К¢.
- прискорення системи К відносно системи К¢.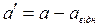 (2.75)
(2.75)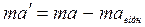
 . Назвемо її силою інерції
. Назвемо її силою інерції  . У векторному вигляді
. У векторному вигляді
 , (2.76)
, (2.76) , що за другим законом Ньютона, пропорцiйна масi кульки i доцентровому прискоренню
, що за другим законом Ньютона, пропорцiйна масi кульки i доцентровому прискоренню  :
:
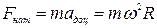 (2.77)
(2.77) на неї має дiяти сила iнерцiї, що в даному випадку називається відцентровою силою F, причому
на неї має дiяти сила iнерцiї, що в даному випадку називається відцентровою силою F, причому (2.78)
(2.78) У положеннi 1 на тіло дiє вiдцентрована сила Fвц, гравiтацiйна Fгр направлена до центра Землi.Сила тяжіння буде дорiвнювати:
У положеннi 1 на тіло дiє вiдцентрована сила Fвц, гравiтацiйна Fгр направлена до центра Землi.Сила тяжіння буде дорiвнювати: .
. .
.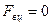 , отже,
, отже,  .
. , (2.79)
, (2.79)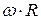 , отже швидкiсть кульки в системi К буде:
, отже швидкiсть кульки в системi К буде: . (2.80)
. (2.80)
 . (2.81)
. (2.81) ,
,  — сила натягу нитки.
— сила натягу нитки. , (2.83)
, (2.83) , сила Корiолiса
, сила Корiолiса  .
. i F к спрямована протилежно вектору нормалi n, силу Корiолiса можна подати як векторний добуток:
i F к спрямована протилежно вектору нормалi n, силу Корiолiса можна подати як векторний добуток: . (2.84)
. (2.84)


