
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основне рiвняння динаміки обертального руху абсолютно твердого тiла
Розглянемо обертання АТТ навколо нерухомої точки О (нехай вона збiгається з центром мас) пiд дiєю зовнiшнiх сил
Продиференціюємо за часом цей вираз:
Оскiльки вектори
де Остаточний вираз має вигляд:
i називається основним рiвнянням динамiки обертального руху АТТ вiдносно нерухомої точки О. Воно свiдчить про те, що похiдна моменту iмпульсу АТТ за часом дорiвнює головному моменту дiючих зовнiшнiх сил. (Моменти
тобто похiдна за часом вiд моменту iмпульсу АТТ вiдносно нерухомої осi обертання дорiвнює головному моменту зовнiшнiх сил вiдносно цiєї осi. Рiвняння (2.43) можна записати iнакше, якщо врахувати вирази (2.41) та (1.50), а також те, що момент iнерцiї I = соnst:
тобто
для обертання навколо нерухомої, осi. Якщо тiло обертається навколо нерухомої точки О, останнiй вираз буде таким:
Цi вирази читаються так: добуток моменту iнерцiї АТТ вiдносно нерухомої точки (або осi) обертання на кутове прискорення дорiвнює головному моменту зовнiшнiх сил вiдносно тiєї ж точки (або осi) обертання. Неважко побачити, що рiвняння (2.42) i (2.45) нагадують записи другого закону Ньютона для поступального руку (див. рiвняння (2.13) та (2.8)). Тiльки роль маси тут вiдiграє момент iнерцiї, роль сили — момент сили Робота, потужнiсть, коефiцiєнт корисної дії Робота Розглянемо матерiальну точку, що рухається довiльною траєкторiєю L пiд дiєю змiнної сили
Розiб’ємо цю траєкторiю на елементарнi перемiщення Тодi скалярний добуток сили
або
де Оскiльки
При При Якщо ж кут Повна робота сили (F) при перемiщеннi з точки 1 в точку 2 буде визначатися сумою елементарних робiт, для обчислення якої слід проiнтегрувати вираз (2.47) або (2.48):
Якщо тiло рухається прямолiнiйно пiд дiєю постiйної сили (тобто F = соnst, соs
тобто
Одиницею роботи в системi СІ є джоуль (Дж). 1Дж=1Н×м. Роботу сили можна знайти графiчно, якщо відомо її залежнiсть вiд перемiщення (рис.2.11). Добуток Для прикладу знайдемо роботу зовнiшньої сили, що розтягує пружину (рис.2.12,а). За третiм законом Ньютона ця сила дорiвнює силi пружностi
Графiк цiєї сили подано на рис. (2.12,б). Робота зовнiшньої сили є додатною i чисельно дорiвнює площi заштрихованого трикутника
Цей же вираз можна одержати з виразу (2.49), пiдставивши вираз (2.51):
Розглянемо роботу у разi обертального руху. Нехай до АТТ прикладено дотичну силу
Оскільки Ftl=M, то
тобто елементарна робота при поворотi тiла на елементарний кут
Зокрема, коли момент дiючої сили є постiйною величиною (М =соnst) з виразу (2.54) маємо, що
Потужнiсть У поняттi роботи час не вiдiграє нiякої ролi. Однак у технiцi дуже суттєво, який час необхiдно витратити на виконання певної роботи. Вiдомссті про це дає потужнiсть. Середньою потужнiстю (N) називається фiзична величина, що визначається вiдношенням всiєї виконаної роботи А до часу
Миттєва потужнiсть (або просто потужнiсть) визначається вiдношенням елементарної роботи
Одиницею вимiрювання потужностi в системi СІ є ват (Вт) 1Вт=1Дж/с. Пiдставляючи у вираз (2.57) вирази для роботи (2.46) i (2.53), одержимо вирази для миттєвої потужностi: — поступального руху
де — обертального руху
де М — момент дiючої сили, Коефiцiєнт корисної дії Характеристикою ефективностi використання технiчного пристрою є його коефiцiєнт корисної дії (ККД). Залежно вiд конкретної задачi, ККД (
де Акор, Nкор. - корисні робота і потужність; Авитр. Nвитр -. витрачені робота і потужність. У реальності в будь-якому процесі присутні тертя, опір та ін., тому завжди Акор. - Авитр, Nкор. - Nвитр і ή-1. ККД виражають у десяткових дробах або у вiдсотках. Наприклад, для авiацiйних двигунiв звичайний ККД — 0,4—0,5 (або 40— 50%), для бортових електрогенераторiв — 0,9—0,95 (або 90—95%). Енергiя. Механiчна енергiя Енергiя — це загальна кiлькiсна мiра руху i взаємодiї всiх видiв матерії. Вiдповiдно до рiзних форм руху i взаємодiї матерiї розглядають рiзнi види енергії: механiчну, внутрiшню, електричну, ядерну та iн. Вiдповiдно до уявлень класичної фiзики енергiя будь-якої системи змiнюється безперервно i може набувати різних значень. Одиницею вимiрювання енергiї є джоуль (Дж) у системi СІ. У механiцi розрiзняють два види енергiї — кiнетичну та потенцiальну — для матерiальної точки
— для механiчної системи
де Кiнетична енергiя Кiнетичною енергією
Скористаємося виразом для елементарної роботи (2.49), другим законом Ньютона (2.8) та виразом для тангенцiального прискорення (1.25):
Оскільки Якщо тiло починає рухатись iз стану спокою, тобто змінює свою швидкість вiд 0 до υ, воно набуде кiнетичну енергiю
Отже, кiнетична енергiя тiла (матерiальної точки) при поступальному русi дорiвнює:
Враховуючи, що iмпульс р = mυ, вираз (2.63) можна записати iнакше, помноживши i поділивши праву частину на m:
Кінетична енергiя системи тiл (матерiальних точок) дорiвнює сумi кiнетичних енергiй окремих елементiв системи тобто є величиною адитивною.
Кiнетична енергiя є величиною вiдносною, i, як i швидкість, залежить вiд системи вiдлiку. Знайдемо вираз для кiнетичної енергії АТТ, що обертається, як уже робилося ранiше, роздiлемо умовно АТТ на малi елементи mi, для кожного з яких кiнетична енергiя за формулою (2.63) дорiвнюватиме
Враховуючи вираз (2.65), а також рiвняння (1.60), запишемо для всього АТТ:
Оскільки
Якщо швидкiсть тiла пiд дiєю сили
Аналогiчне вiдбувається при обертальному русi, коли кутова швидкiсть АТТ змiнюється вiд
Зрозумiло, що додатня робота приводить до збiльшення кiнетичної енергiї тiла, а вiд’ємна робота — до зменшення кiнетичної енергiї Потенцiальна енергiї Потенцiальною енергiєю Загалом взаємодiя мiж тiлами вiдбувається або при безпосередньому контактi, або на вiдстанi, за рахунок сил поля. Сили за їх властивостями можна подiлити на два класи. Для сил одного класу робота при перемiщеннi тiла мiж двома точками не залежить вiд траєкторiї руху, а для сил другого класу — залежить вiд траєкторiї руху тiла. Сили, робота яких не залежить вiд форми траєкторiї руху тiла i визначається тільки початковою i кiнцевою точками траєкторiї, називаються консервативними (наприклад гравiтацiйна сила, електростатична сила). Саме цi сили можна описати за допомогою потенцiальної енергii. Сили, робота яких залежить вiд траєкторiї руху тiла, називаються неконсервативними (наприклад, сили тертя). Для цих сил не iснує поняття потенцiальної енергiї. Область простору, в якiй дiють сили, називається полем сил (або просто полем). Поля, в яких дiють консервативнi сили, називаються потенцiальними полями. Тiло, що перебуває в потенцiальному полi, має потенцiальну енергiю За означенням, потенцiальна енергiя тiла в даному його положеннi чисельно дорiвнює роботi, яку виконують дiючi на тiло консервативнi сили при перемiщеннi його з цього положення в те, де потенцiальна енергiя умовно приймається рiвною нулю. З цього означення можна зробити два висновки.
По-перше, робота консервативних сил, що дiють на тiло в потенцiальному полi, дорiвнює зменшенню потенцiальної енергiї тiла. Дiйсно, оскільки пiд дiєю консервативних сил тiло перемiщується з точки з бiльшою потенцiальною енергiєю
По-друге, значення потенцiальна енергiя залежить вiд того, яке положення тiла умовно взяте за нуль (вибiр нульового рiвня потенцiальної енергiї називається нормуванням потенцiальної енергії). Причому в разi замiни одного нульового рiвня на iнший потенцiальна енергiя змiнюється на сталу величину. Наприклад, вiзьмемо за нульове положення тiла в точцi l (рис.2.14,а). Тодi в положенні 2 потенцiальна енергiя тiла дорiвнюватиме Роботу А, можна позначити як довiльну константу С i записати в загальному виглядi
Таким чином, потенціальна енергiя визначається не однозначно, а з точнiстю до довiльної сталої. Довiльнiсть вибору сталої не впливає на фiзичнi висновки, оскiльки вони характеризуються не абсолютним значенням потенцiальної енергiї, а й змiною, а саме Потенцiальна енергiя залежить вiд характеру взаємодiї тiл, тому єдиної формули для неї, як для кiнетичної енергiї, немає. Крiм того, оскiльки початок вiдлiку вибирається довiльно, потенцiальна енергiя може мати вiд’ємнi значення (кiнетична енергiя завжди додатня). Наприклад, якщо за нуль прийняти потенцiальну енергiю тiла, що пребуває на поверхнi Землi, то потенцiальна енергiя тiла, пiднятого на висоту h 1 буде Запишемо тепер математичний критерiй (тобто ознаку) потенцiальностi поля консервативних сил. Нехай тiло рухалося замкненою траєкторією 1—1 (рис.2.14,б). Оскiльки на нього дiяли консервативнi сили, їх робота в цьому замкненому контуру (позначимо його L) дорiвнює нулю. Математично це записується, з урахуванням рiвняння (2.46), так:
У математиці інтеграл вигляду
тобто циркуляцiя вектора сили
|
||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 862; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.205.146 (0.059 с.) |
 . Вiдповідно до виразу (2.39) його момент iмпульсу
. Вiдповідно до виразу (2.39) його момент iмпульсу

 та
та 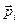 , колiнеарнi, їх векторний добуток дорiвнює нулю. Тодi з урахуванням формули (2.13) останнiй вираз стане:
, колiнеарнi, їх векторний добуток дорiвнює нулю. Тодi з урахуванням формули (2.13) останнiй вираз стане:
 — головний момент зовнiшнiх сил, що дiють на АТТ.
— головний момент зовнiшнiх сил, що дiють на АТТ. (2.42)
(2.42) і
і  i
i 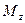 на цю вiсь:
на цю вiсь: (2.43)
(2.43)
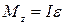 (2.44)
(2.44)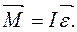 (2.45)
(2.45) . Якщо при поступальному русi причиною змiни руху були дiючi сили
. Якщо при поступальному русi причиною змiни руху були дiючi сили 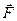 , то при обертальному русi причиною змiни обертання є момент дiючих сил
, то при обертальному русi причиною змiни обертання є момент дiючих сил 
 так, щоб на кожному такому перемiщеннi дiючу силу можна було б вважати постiйною.
так, щоб на кожному такому перемiщеннi дiючу силу можна було б вважати постiйною. на перемiщення
на перемiщення  буде називатись елементарною роботою
буде називатись елементарною роботою 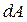 :
: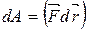 , (2.46)
, (2.46) (2.47)
(2.47)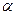 — кут мiж векторами
— кут мiж векторами  .
. ,тобто є проекцiєю сили
,тобто є проекцiєю сили  до траєкторiї в даному мiсцi, то вираз (2.47) можна записати як
до траєкторiї в даному мiсцi, то вираз (2.47) можна записати як (2.48)
(2.48) , тобто кут
, тобто кут 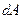 ; 0. Вiдповiдну силу часто називають рушійною силою (наприклад, сила тяги лiтака або ракети).
; 0. Вiдповiдну силу часто називають рушійною силою (наприклад, сила тяги лiтака або ракети). , тобто коли кут
, тобто коли кут 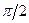 то
то  (2.49)
(2.49)
 (2.50)
(2.50)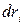 на
на  , (див. рис. 2.11), що визначає елементарну роботу
, (див. рис. 2.11), що визначає елементарну роботу  , є площиною прямокутника з основою
, є площиною прямокутника з основою  i висотою
i висотою  . Такий пiдхiд часто математично спрощує обчислення роботи.
. Такий пiдхiд часто математично спрощує обчислення роботи. =
=  , але протилежна їй за напрямком:
, але протилежна їй за напрямком:  , тому
, тому
 (2.51)
(2.51)
 (2.52)
(2.52)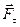 , пiд дiєю якої воно повернулося на малий кут
, пiд дiєю якої воно повернулося на малий кут  (рис. 2.13). При цьому точка прикладання сили перемiстилася на
(рис. 2.13). При цьому точка прикладання сили перемiстилася на  . Як вiдомо, переміщення
. Як вiдомо, переміщення  :
: 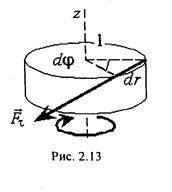

 (2.53)
(2.53) чисельно дорiвнює добутку моменту дiючої сили на цей кут. Якщо ж тiло повернулося на певний кут
чисельно дорiвнює добутку моменту дiючої сили на цей кут. Якщо ж тiло повернулося на певний кут  до положення
до положення  , то повну роботу в обертальному русi знайдемо шляхом iнтегрування виразу (2.53):
, то повну роботу в обертальному русi знайдемо шляхом iнтегрування виразу (2.53): (2.54)
(2.54) (2.55)
(2.55) , за який ця робота була виконана:
, за який ця робота була виконана: (2.56)
(2.56) , за який вона виконана:
, за який вона виконана: (2.57)
(2.57) (2.58)
(2.58) — миттєва швидкiсть тiла;
— миттєва швидкiсть тiла; (2.59)
(2.59)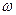 — миттєва кутова швидкiсть обертання АТТ.
— миттєва кутова швидкiсть обертання АТТ.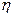 ) визначається через рiзні фiзичні величини, але завжди як вiдношення “корисних результатів” до “витрат”. У механiцi це може бути записано так:
) визначається через рiзні фiзичні величини, але завжди як вiдношення “корисних результатів” до “витрат”. У механiцi це може бути записано так: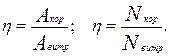 , (2.60)
, (2.60) . Повна механiчна енергiя дорівнює їхній сумі:
. Повна механiчна енергiя дорівнює їхній сумі: (2.61)
(2.61) , (2.62)
, (2.62) та
та  вiдповiдно кiнетична i потенцiальна енергiя i —го елемента системи. Розглянемо кожний з цих видiв механiчної енергiї.
вiдповiдно кiнетична i потенцiальна енергiя i —го елемента системи. Розглянемо кожний з цих видiв механiчної енергiї. . Тодi кiнетична енергiя тiла змiнилася на
. Тодi кiнетична енергiя тiла змiнилася на  . Зрозумiло, що ця змiна кiнетичної енергiї вiдбулася за рахунок виконання силою
. Зрозумiло, що ця змiна кiнетичної енергiї вiдбулася за рахунок виконання силою  ,
, ,
, , а
, а  , то
, то  .
. .
. (2.63)
(2.63) . (2.64)
. (2.64) (2.65)
(2.65) .
.
 є моментом iнерції I всього тiла, остаточно будемо мати для кiнетичної енергії обертального руху АТТ
є моментом iнерції I всього тiла, остаточно будемо мати для кiнетичної енергії обертального руху АТТ (2.66)
(2.66) до
до  то виконана при цьому робота сили дорiвнює змiнi кiнетичної енергiї тiла:
то виконана при цьому робота сили дорiвнює змiнi кiнетичної енергiї тiла: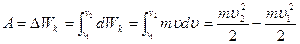 (2.67)
(2.67) до
до  :
: (2.68)
(2.68) називається енергiя взаємодії тiл (або їх частин), що залежить вiд їх взаємного розташування.
називається енергiя взаємодії тiл (або їх частин), що залежить вiд їх взаємного розташування. в точку з меншою потенцiальною енергiєю
в точку з меншою потенцiальною енергiєю  -
-  (2.69)
(2.69)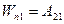 . Якщо ж узяти за нульове положення тiла в точцi l ¢, то його потенцiальна енергiя в точцi 2 буде
. Якщо ж узяти за нульове положення тiла в точцi l ¢, то його потенцiальна енергiя в точцi 2 буде  . Оскiльки сили консервативні, то робота вздовж траєкторiї 2- l ¢ дорiвнює роботi вздовж траєкторiї 2 — 1 — l¢, тобто
. Оскiльки сили консервативні, то робота вздовж траєкторiї 2- l ¢ дорiвнює роботi вздовж траєкторiї 2 — 1 — l¢, тобто  , або
, або 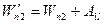
 (2.70)
(2.70)
 . Зрозумiло, що для зручностi найчастiше покладають С = 0.
. Зрозумiло, що для зручностi найчастiше покладають С = 0. , а тiло, що перебуває на днi шахти глибиною h 2, буде
, а тiло, що перебуває на днi шахти глибиною h 2, буде  .
.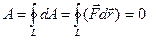 .
. називається циркуляцiєю вектора
називається циркуляцiєю вектора 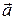 вздовж замкненого контура L. Отже для поля консервативних сил маємо такий математичний критерiй його потенцiальностi:
вздовж замкненого контура L. Отже для поля консервативних сил маємо такий математичний критерiй його потенцiальностi: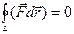 , (2.71)
, (2.71)


