
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Динамiчнi характеристики обертального руху абсолютно твердого тiла (АТТ)Содержание книги
Поиск на нашем сайте З’ясуємо особливостi обертального руху АТТ з динамiчноiї точки зору, розглядаючи такий дослiд. Вiзьмемо тiло у виглядi хрестовини, яке закрiплене на горизонтальнiй осi i може обертатися навколо неї (так званий маятник Обербека). На хрестовинi симетрично осi обертання можуть закрiплятись однаковi тягарцi масами Якщо ж нитку намотати на шкiв з дiаметром R2, що менший за R1, то кутове прискорення зменшиться ( Продовжимо дослiд. Залишимо нитку на другому шкiвi, але змiнимо розташування тягарцiв
Третьою характеристикою обертального руху АТТ є момент iмпульсу (  ). Визначимо цi характеристики, розглядаючи обертання АТТ навколо нерухомої точки О та навколо нерухомої осi, що проходить через цю точку обертання. ). Визначимо цi характеристики, розглядаючи обертання АТТ навколо нерухомої точки О та навколо нерухомої осi, що проходить через цю точку обертання.
Момент сили Моментом сили
Визначення моменту сили дано так, щоб кутове прискорення i кутова швидкiсть, якi виникають внаслiдок дiї моменту сили, збiгалися за напрямком з цим моментом. Тобто вектор Модуль моменту сили дорiвнює:
де Якщо на тiло дiє кiлька сил, можна знайти суму моментiв цих сил відносно точки обертання О. Ця сума називається головним моментом зовнiшнiх сил вiдносно точки обертання О:
Моментом сили вiдносно осi обертання z називають проекцiю вектора
Якщо вектор
Нехай на тiло дiють двi сили, якi рiвнi за модулем, а спрямованi протилежно вздовж паралельних прямих. Такi сили називаються парою сил (рис. 2.4). Згiдно з виразом (2.20), момент пари сил вiдносно точки О
а його модуль
Оскільки  то то
де l = l 1 +l 2 - плече пари, тобто найкоротша вiдстань мiж прямими, вздовж яких дiють сили одержаний вираз не залежить вiд розташування точки О. Узагалі, щоб тiло, на яке дiють рiзнi зовнiшнi сили, не оберталося, тобто знаходилось в рiвновазi, сумарний момент цих сил має дорiвнювати нулю:
Момент iнерції
Моментом iнерції І матерiальної точки вiдносно деякої осi z, називається добуток маси матерiальної точки mi на квадрат її вiдстанi
Момент iнерцiї всього тiла вiдносно деякоiї осi Z дорівнює сумi моментiв iнерції всiх його точок вiдносно цiєї осi:
Ця величина скалярна, одиниця вимiрювання в системi СІ — кг м2. Момент iнерцiї має кожне тiло, незалежно вiд свого руху. Подiбно до того, як тiло має масу незалежно вiд свого стану руху чи спокою, воно має i момент iнерцiї вiдносно будь-якої осi незалежно вiд того, обертається воно навколо цiєї осi чи нi. Як виходить iз означення (2.29), момент iнерцiї залежить не тiльки вiд маси тiла, але й вiд того, як ця маса розподiлена за об’ємом тiла. Враховуючи, що
де ρ — густина речовини у вибраному об’ємi dV, r — вiдстань цього об’єму вiд осi, вiдносно якої обчислюється момент iнерцiї. Знаходження цього iнтеграла загалом випадках є досить складним. Задача значно спрощується, якщо розглядати однорiднi тiла правильної форми. Наведемо вирази для моментiв iнерцiї деяких таких тiл: · момент iнерцiї диска (цилiндра) з радiусом R вiдносно осi симетрiї:
· момент iнерцiї обруча (тонкостiнного порожнього цилiндра) з радiусом R вiдносно осi симетрії:
· момент iнерції суцiльної кулi з радiусом R вiдносно осi, що проходить через центр кулi:
· момент iнерцiї однорiдного стрижня довжиною l вiдносно осi, що проходить через його середину перпендикулярну до l:
· те ж саме вiдносно осi, що проходить через кiнець стрижня:
Як бачимо, момент iнерцiї тiла залежить не тiльки вiд маси, форми i розмiрiв тiла, але й вiд розташування тiла вiдносно осi. Можна обчислити момент iнерцiї тiла вiдносно будь-якої осi. Для цього зручно використовувати теорему Штейнера: момент iнерцiї тiла І вiдносно довiльноiї осi z ’дорiвнює сумi моменту інерції тiла I0, вiдносно осi, що проходить через його центр мас паралельно данiй осi z ’, i добутку маси тiла m на квадрат вiдстанi d мiж осями (рис. 2.6):
Момент iмпульсу Моментом iмпульсу
Напрямок вектора
Якщо через точку О проходить вiсь z, навколо якої точка обертається, то моментом iмпульсу матерiальної точки вiдносно осi називається проекцiя моменту iмпульсу вiдносно точки О на цю вiсь (рис. 2.7,б):
Розглянемо тепер АТТ, що обертається навколо нерухомої осi z. Як i в попередньому пунктi, представимо його як систему N матерiальних точок масою m i.Тодi момент iмпульсу АТТ вiдносно точки О, через яку проходить вiсь обертання, дорiвнюватиме геометричнiй сумi моментiв iмпульсiв його точок вiдносно цiєї точки обертання О:
де
Моментом iмпульсу АТТ вiдносно осi обертання Z, що проходить через точку О, називається проекцiя вектора моменту iмпульсу відносно цiєї точки на вiсь (рис. 2.8,б).
Виходячи з виразiв (2.38) та (2.39), можемо записати
Iз мiркувань симетрiї зрозумiло, що для однорiдного тiла, симетричного вiдносно осi обертання, вектор
Оскiльки для обертального руку
тобто момент iмпульсу АТТ вiдносно осi обертання дорiвнює добутку моменту iнерцiї тiла вiдносно тiєї ж осi на кутову швидкість обертання:
даний вираз не залежить вiд положення на осi обертання точки О, вiдносно якої визначався момент iмпульсу.
|
|||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 709; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |

 кожний. На горизонтальнiй осi хрестовини є два шкiви рiзних дiаметрів R1 і R2. Намотаємо на шкiв дiаметром R1 нитку, другий кiнець якої з тягарцем перекинемо через нерухомий блок (Бл.). Пiд дiєю тягарця, тобто сили
кожний. На горизонтальнiй осi хрестовини є два шкiви рiзних дiаметрів R1 і R2. Намотаємо на шкiв дiаметром R1 нитку, другий кiнець якої з тягарцем перекинемо через нерухомий блок (Бл.). Пiд дiєю тягарця, тобто сили 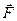 , хрестовина почне обертатися з кутовим прискоренням
, хрестовина почне обертатися з кутовим прискоренням  (рис. 2.2,а).
(рис. 2.2,а). -
-  ) (рис. 2.2,б). Це означає, що одна й та ж сила, залежно вiд точки прикладання, спричиняє рiзну обертальну дiю. Тому в обертальному русi вводиться поняття моменту сили (
) (рис. 2.2,б). Це означає, що одна й та ж сила, залежно вiд точки прикладання, спричиняє рiзну обертальну дiю. Тому в обертальному русi вводиться поняття моменту сили ( ).
).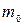 на стрижнях хрестовини, закрiпивши їх ближче до центра (рис. 2.2,в). При цьому кутове прискорення обертання хрестовини теж змiниться. Отже, кутове прискорення залежить не тiльки вiд маси, а й вiд розподiлу маси тiла, що обертається. Характеристика, що визначає цю залежнiсть, називається моментом iнерцiї тiла (І).
на стрижнях хрестовини, закрiпивши їх ближче до центра (рис. 2.2,в). При цьому кутове прискорення обертання хрестовини теж змiниться. Отже, кутове прискорення залежить не тiльки вiд маси, а й вiд розподiлу маси тiла, що обертається. Характеристика, що визначає цю залежнiсть, називається моментом iнерцiї тiла (І).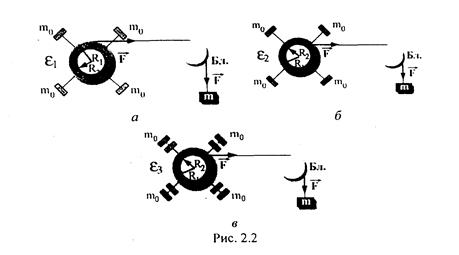
 , проведеного з точки О в точку прикладання сили, на цю силу
, проведеного з точки О в точку прикладання сили, на цю силу 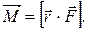 (2.20)
(2.20)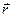 i
i  (2.21)
(2.21)
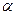 — кут мiж векторами
— кут мiж векторами  — перпендикуляр, проведений з точки О на лiнiю дiї сили
— перпендикуляр, проведений з точки О на лiнiю дiї сили 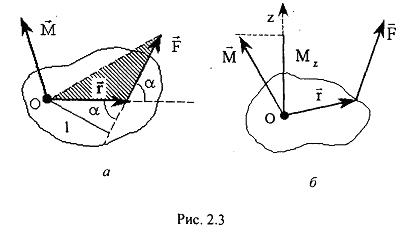
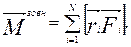 (2.22)
(2.22) (2.23)
(2.23)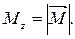 (2.24)
(2.24)
 (2.25)
(2.25)
 (2.26)
(2.26) (2.27)
(2.27) Уявно розiб’ємо АТТ на малi елементи об’ємом
Уявно розiб’ємо АТТ на малi елементи об’ємом  та масою m i якi можна вважати матерiальними точками (тобто представимо АТТ як систему матерiальних точок з масою m i).
та масою m i якi можна вважати матерiальними точками (тобто представимо АТТ як систему матерiальних точок з масою m i).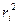 , вiд цiєї осi (рис.2.5):
, вiд цiєї осi (рис.2.5): (2.28)
(2.28) (2.29)
(2.29) та переходячи вiд додавання до iнтегрування перепишемо вираз (2.29):
та переходячи вiд додавання до iнтегрування перепишемо вираз (2.29): (2.30)
(2.30)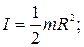 (2.31)
(2.31) (2.32)
(2.32)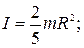 (2.33)
(2.33) (2.34)
(2.34) (2.35)
(2.35)
 (2.36)
(2.36)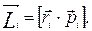 (2.37)
(2.37) .
.

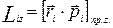 (2.38)
(2.38) (2.39)
(2.39) — радiус-вектор кожної точки тiла вiдносно точки обертання О,
— радiус-вектор кожної точки тiла вiдносно точки обертання О, 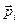 — iмпульс кожної точки тiла. Взагалі, коли тiло несиметричне, вектор
— iмпульс кожної точки тiла. Взагалі, коли тiло несиметричне, вектор  може не збiгатися з вектором кутової швидкостi
може не збiгатися з вектором кутової швидкостi  (рис. 2.8,а).
(рис. 2.8,а).

 (2.40)
(2.40)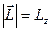 (рис.2.9). Знайдемо модуль L, враховуючи, що
(рис.2.9). Знайдемо модуль L, враховуючи, що  а куг
а куг  завжди дорiвнює 90о.
завжди дорiвнює 90о.
 , то з урахуванням виразiв (2.28) та (2.39) можна записати:
, то з урахуванням виразiв (2.28) та (2.39) можна записати:
 (2.41)
(2.41)


