
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Матеріальною точкою (МТ) називають тiло, геометричними розмiрами якого в умовах конкретної задачi можна знехтувати.Содержание книги
Поиск на нашем сайте
Абсолютно твердим тiлом (АТТ) називають тiло, у якого вiдстань мiж будь-якими двома точками нiколи не змiнюється. Іншими словами, це тіло, деформацією якого можна знехтувати. Основна задача механіки- визначення положення тіла в будь який момент часу.
КIНЕМАТИКА Кiнематика — роздiл механiки, в якому вивчається рух тiл, не встановлюючи причин, що викликали цей рух. Сам термiн походить вiд грецького слова „кiнета”, що означає рух. За законами i залежностями, встановленими в кiнематицi, визначаються параметри польоту лiтальних апаратiв, виконуються розрахунки передач рухiв у рiзних авiацiйних механiзмах та iн. 1.1. Механiчний рух. Система вiдлiку Механiчним рухом називається змiна положення тiла в просторi вiдносно iнших тiл. Це все свідчить, що механiчний рух є вiдносним. Дiйсно, будь-яке тiло може бути нерухомим вiдносно одних тiл i рухається вiдносно iнших. Разом з тим цей рух є абсолютним, оскiльки завжди можна вказати, таке тiло, вiдносно якого дане „нерухоме” тiло рухається, тобто абсолютно нерухомих тiл в природi не iснує. Отже, починаючи дослiджувати рух якогось тiла, слід визначити, вiдносно якого iншого тiла вiн буде розглядатися. Тiло, вiдносно якого розглядається рух, називається тiлом вiдлiку. Для математичного описування руху з тiлом вiдлiку необхiдно зв’язати систему координат. Як вiдомо, iснує багато рiзних систем координат (полярна, цилiндрична, сферична та iн.). Найбiльш поширеною є прямокутна декартова система координат. Слiд звернути увагу, що iснують два види декартових систем: права (рис. 1.1) та лiва (рис.1.2), якi розрiзняють за допомогою правила гвинта: якщо обертати ручку гвинта вiд додатнього кiнця осi ОХ до додатнього кiнця осi ОУ, то в правiй системi координат гвинт буде поступально рухатись у додатньому напрямку осi ОZ, а в лiвiй системi — у вiд’ємному напрямку. У фiзицi здебiльшого застосовується права система. Перемiщення тiл вiдбувається з плином часу, тому для описування руху слід мати також годинник. Тiло вiдлiку, повязана з ним система координат та годинник становлять систему вiдлiку.
1.2. Способи описування руху матерiальноiї точки. Основна (пряма) задача кінематик Важливо зазначити, що в класичнiй механiцi загальновизначеною є концепцiя простору i часу, розроблена Ньютоном. Вiдповiдно до цiєї концепцiї простiр i час розглядаються як такi, що не пов’язанi нi мiж собою, нi з рухом тiл. Iншими словами, в класичнiй механiцi простiр i час вважаються абсолютними та iснуючими не залежно один вiд одного. Тому i хiд годинникiв (тобто плин часу) не залежить вiд системи вiдлiку i всюди є однаковим. Розглянемо спочатку рух найпростiшого об’єкту — матерiальної точки. Визначимо деякi поняття, якi використовують пiд час описування цього руху.
Траєкторiя — це уявна лiнiя, вздовж якої рухається матеріальна точка (рис. 1.3). Шлях (∆S або S) — це довжина траєкторiї (рис. 1.3). Шлях — величина скалярна, в системi СІ вимiрюється в метрах (м). Перемiщення ∆r — це найкоротша вiдстань мiж початковою i кiнцевою точками траєкторїi (рис. 1.4). Перемiщення — величина векторна, має напрямок вiд початковоїi до кiнцевої точки траєкторiї; в системi СІ вимiрюється в метрах.
Радiус-вектор може бути записаний через його проекцiї
та за модулем:
де
де
, (1.3)
У фізиці прийнято модуль будь-якого вектора Зрозумiло, що пiд час руху матерiальної точки‚ її радіус-вектор, шлях та координати з часом змiнюються. Вiдповiдно до цього в кiнематицi використовуються три способи описування руху: — векторний, коли вiдоме рiвняння залежностi радіус-вектора точки вiд часу:
— траєкторний, коли вiдоме рiвняння руху точки вздовж траєкторії:
— координатний, коли вiдомi рiвняння руху точки в декартових координатах: х = х(t), у =у(t), z=z(t). (1.7) Рiвняння (1.5), (1.6), (1.7) називаються кінематичними рiвняннями руху. Основна (пряма) задача кiнематики полягає в тому, щоб за кiнематичними рiвняннями руху знайти положення матеріальної точки в просторi i кiнематичнi характеристики руху в будь-який момент часу. 1.3. Кiнематичнi характеристики поступального руху матерiальної точки До кiнематичних характеристик поступального руху вiдносяться: перемiщення, швидкiсть та прискорення. Перемiщення Нехай у момент часу t матерiальна точка пребувала в положеннi 1, а за деякий промiжок часу ∆t — в положеннi 2 (рис. 1.6,а). Проведемо радiус-вектори
тобто вектор перемiщення являє собою змiну (прирiст) радіуса-вектора за часом. З урахуванням (1.3) вектор ∆ r можна записати через прирiст координат матерiальної точки (∆х, ∆у, ∆z) за час ∆t:
а його модуль як
Як видно з рис. (1.6,б) вектор перемiщення збiгається з хордою, що стягує вiдповiдну дiлянку траєкторії. Тому завжди, крiм прямолiнiйного руху, модуль вектора перемiщення менший, нiж шлях, пройдений за той же промiжок часу:
Тепер будемо зменшувати промiжок часу ∆t до достатньо малого значення, яке назвемо елементарним i позначимо dt. При цьому вiдбудеться також мале перемiщення, яке називатиметься відповiдно елементарним перемiщенням d dr = dS (1.12) За напрямком d
Швидкість Розрiзняють швидкiсть середню i миттєву. Середньою швидкiстю перемiщення (
Вектор Будемо нескiнченно зменшувати промiжок часу, направляючи його до нуля ( Ця границя i визначає швидкiсть руху в даному мiсцi траєкторiї в даний момент часу, тобто миттєву швидкiсть (при цьому точки 1 i 2 на рис. 1.7,а будуть нескiнченно наближатися одна до одної).
Враховуючи (1.12) одержимо:
|
||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 343; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.163.134 (0.008 с.) |



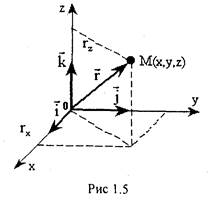 У декартовiй системi координат положення матерiальної точки М може бути задане не тiльки трьома координатами (х, у, z), а й за допомогою радiуса-вектора. Радiус — вектором
У декартовiй системi координат положення матерiальної точки М може бути задане не тiльки трьома координатами (х, у, z), а й за допомогою радiуса-вектора. Радiус — вектором  точки називається вектор, який проведено з початку координат у дану точку (рис. 1.5).
точки називається вектор, який проведено з початку координат у дану точку (рис. 1.5).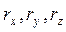 на вiдповiднi координатнi осi:
на вiдповiднi координатнi осi: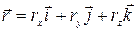 (1.1)
(1.1) , (1.2)
, (1.2)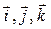 - одиничні вектори (орти) відповідних осей координат:
- одиничні вектори (орти) відповідних осей координат: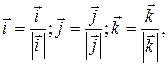

 Оскільки
Оскільки  формули (1.1) і (1.2) можуть бути записані ще й так:
формули (1.1) і (1.2) можуть бути записані ще й так: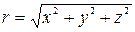 . (1.4)
. (1.4)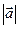 позначати а.
позначати а.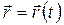 (1.5)
(1.5)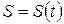 (1.6)
(1.6) і
і 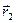 в точки 1 i 2. Тодi вектор перемiщення визначиться як
в точки 1 i 2. Тодi вектор перемiщення визначиться як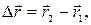 (1.8)
(1.8)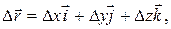 (1.9)
(1.9)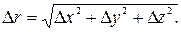 (1.10)
(1.10)
 (1.11)
(1.11)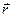 i матерiальна точка пройде досить малий, тобто елементарний шлях d S. Ясно, що iз зменшенням ∆t значення ∆r буде все бiльше наближатися до ∆S. Тобто при (
i матерiальна точка пройде досить малий, тобто елементарний шлях d S. Ясно, що iз зменшенням ∆t значення ∆r буде все бiльше наближатися до ∆S. Тобто при ( ) можна вважати, що
) можна вважати, що , тодi у векторному виглядi можна записати (при
, тодi у векторному виглядi можна записати (при 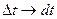 ):
):
 ) за промiжок часу ∆t називається векторна величина, що дорiвнює вiдношенню вектора перемiщення до цього промiжку часу:
) за промiжок часу ∆t називається векторна величина, що дорiвнює вiдношенню вектора перемiщення до цього промiжку часу: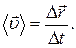 (1.13)
(1.13)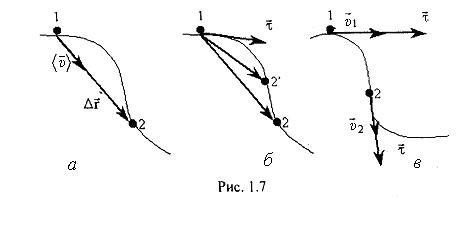
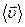 спрямований так, як i вектор
спрямований так, як i вектор 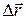 (рис. 1.7,а).
(рис. 1.7,а). перестає змiнюватися. Тобто iснує певна границя, до якої прямує вiдношення
перестає змiнюватися. Тобто iснує певна границя, до якої прямує вiдношення 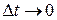 .
. (1.14)
(1.14)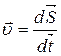 (1.15)
(1.15)


