
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Яка відносна величина характеризує співвідношення між складовими частинами цілого?Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
а) Відносна величина структури; б) Відносна величина координації; в) Відносна величина порівняння; г) Відносна величина інтенсивності. 7. Середню гармонічну використовують: а) тоді, коли загальний обсяг варіюючої ознаки для усієї сукупності становить суму індивідуальних значень усередненої ознаки; б) для узагальненої характеристики тоді, коли відомі окремі значення досліджуваної ознаки і обсяги явищ, а частоти невідомі; в) для узагальненої характеристики тоді, коли відомі окремі значення досліджуваної ознаки і обсяги явищ; 8. Коефіцієнт варіації можна розрахувати на основі: а) середнього квадратичного відхилення; б) середнього лінійного відхилення; в) варіаційного розмаху; г) середньої арифметичної зваженої. 9. Частотою називається: а) окремі значення групувальної ознаки; б) загальні значення групувальної ознаки; в) кількість одиниць спостереження, що мають однакове значення ознаки; В яких одиницях виражаються відносні показники, коли базова величина приймається за 1000? а) У коефіцієнтах; б) У процентах; в) У проміле; г) У продециміле; Чому дорівнює алгебраїчна сума відхилень індивідуальних значень ознаки від середньої арифметичної? а) Постійній величині; б) Нулю; в) Від'ємній величині; г) Додатній величині.
Практична робота №4 Тема: "Кореляція" Мета роботи: З’ясувати сутність, значення, область застосування кореляційного аналізу. Завдання 1. На основі даних підприємств побудуйте кореляційне поле, рівняння зв’язку та розрахуйте коефіцієнт кореляції, детермінації при прямолінійній залежності між ознаками. Проаналізуйте одержані результати. Методика виконання: При прямолінійній залежності парний кореляційний зв’язок між ознаками визначають за рівнянням прямої:
де y - результативна ознака (урожайність); x -факторна ознака (розмір затрат на 1 га); a -початок відліку або значення y при x який дорівнює нулю; b - коефіцієнт регресії рівняння зв’язку, який показує, як змінюється результативна ознака залежно від зміни на одиницю факторної ознаки. Дане рівняння можна розв’язувати способом найменших квадратів. Розв’язок рівняння зводиться до визначення невідомих параметрів a та b. Для їх визначення необхідно розв’язати систему двох нормальних рівнянь способом підстановки:
де n- кількість спостережень. Параметри a і b можна розв’язати,використовуючи формули:
Обчислений коефіцієнт регресії показує, що при збільшені розміру затрат на 1 га на 1 грн урожайність культури збільшується на________ Підставивши в рівняння знайдені параметри і фактичні значення факторної ознаки, дістанемо теоретичні рівні врожайності культури. Якщо, то параметри рівняння визначенні правильно.
Таблиця 1 Вихідні та розрахункові дані для обчислення кореляційного рівняння зв’язку та визначення коефіцієнта кореляції
Коефіцієнт кореляції визначається за формулою:
де r - коефіцієнт кореляції; x -середня величина факторної ознаки; y -середня ознака результативної ознаки; xy -середня величина з добутку ознак та;
Коефіцієнт детермінації:
Висновок: Розрахунковий коефіцієнт кореляції свідчить про те, що між показниками врожайності та розміром затрат на 1 га існує в даному випадку __________, _________ зв’язок. Завдання 2. На основі вихідних даних побудувати кореляційне поле, розв’язати рівняння зв’язку при криволінійній залежності між ознаками. Визначити кореляційне відношення, одержанні результати проаналізувати, а також визначити вірогідність кореляційного відношення.
Методика виконання 1. Якщо криволінійна залежність має форму параболи другого порядку, зв’язок між результативною і факторною ознакою виражають таким рівнянням:
де x - значення факторної ознаки; a, b, c- параметри рівняння. Складають систему рівнянь:
Для спрощення розв’язку,замість значень x вводять відхилення від середньої
а система рівнянь:
Оскільки використовуючи спосіб найменших квадратів ми маємо
Середнє значення факторної ознаки за формулою:
Підставимо табличне значення в систему рівнянь. З другого рівняння визначимо параметр b. Перше і третє рівняння розділимо на коефіцієнти при a. В першому рівнянні на n, в третьому Підставивши в рівняння відповідні значення відхилень та їх квадрати, обчислимо теоретичні рівні результативної ознаки Таблиця 2 Вихідні та розрахункові дані для визначення параметрів рівняння параболи
2. Якщо криволінійна зеленість між результативною і факторною ознакою має гіперболічний характер, розв’язуємо рівняння гіперболи:
де x -значення факторної ознаки. a i b Параметри рівняння регресії. Для визначення параметрів а і в способом найменших квадратів складають систему рівнянь:
Таблиця 3 Вихідні та розрахункові дані для визначення рівняння гіперболи
Підставивши дані таблиці 3 у рівняння, знайдемо параметри a i b. Підставивши в рівняння, значення факторної ознаки х, дістанемо теоретичні значення результативної ознаки 3. Тісноту зв’язку при криволінійних формах залежності визначають за допомогою кореляційного відношення:
де
Можна використати спрощену робочу формулу кореляційного відношення:
Середнє значення результативної ознаки визначають за формулою:
3. Вірогідність коефіцієнта парної кореляції визначають за t- критерієм, який обчислюють за формулою:
де r- коефіцієнт кореляції; n- вибіркова сукупність;
Середня помилка коефіцієнта кореляції визначається:
Якщо Ключові терміни і поняття: Кореляція, кореляційне поле, коефіцієнт регресії, лінійний коефіцієнт кореляції, коефіцієнт детермінації, кореляційний зв'язок, поле графіка, функціональний зв'язок, стохастичний зв'язок.
Тестові завдання: 1. Множинною кореляцією називають: а)кореляція,за допомогою якої вивчається вплив результативної ознаки на факторну; б)кореляція,за допомогою якої вивчається вплив на результативну ознаку 2-ох і більше факторних ознак; в)кореляція,яка вивчає лише факторні ознаки. Кореляційне поле,це а)фактичне відображення точок резулдьтативної і факторної ознак в системі координат; б)порівняння результативної і факторної ознак в системі координат; в)зображення в системі координат точок,які відповідають розміщенню підприємств в ранжированому ряду. 3. Важливою характеристикою кореляційного зв’язку є: а)лінія прогресії б) лінія регресії в) лінія дескреції г) всі відповіді неправильні 4. Серед мір щільності зв’язку найпоширенішим є коефіцієнт:
а) варіації б) детермінації в) кореляції
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 489; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.143.67.105 (0.011 с.) |

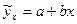 ,
, - теоретичні значення результативної ознаки;
- теоретичні значення результативної ознаки;

 ,
,  .
.
 -середнє квадратичне відхилення факторної ознаки;
-середнє квадратичне відхилення факторної ознаки; -середнє квадратичне відхилення результативної ознаки.
-середнє квадратичне відхилення результативної ознаки.
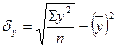

 %
% ,
,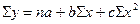


 . Рівняння буде мати такий вигляд:
. Рівняння буде мати такий вигляд: ,
,
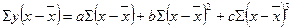
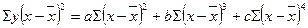
 , які дорівнюють нулю, то система рівнянь спрощується:
, які дорівнюють нулю, то система рівнянь спрощується:


 .
. . З більшого рівняння віднімемо менше, визначимо параметр c. Підставивши в одне з попередніх рівнянь значення параметра c, визначимо a.
. З більшого рівняння віднімемо менше, визначимо параметр c. Підставивши в одне з попередніх рівнянь значення параметра c, визначимо a.


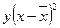
 ,
, .
.

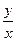
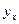 .
.
 - між групова дисперсія;
- між групова дисперсія; - загальна дисперсія.
- загальна дисперсія.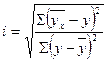


 - середня помилка коефіцієнта кореляції;
- середня помилка коефіцієнта кореляції; - фактичне значення t- критерію.
- фактичне значення t- критерію.
 перевищує табличне значення
перевищує табличне значення  , зв'язок між ознаками вірогідний. Якщо
, зв'язок між ознаками вірогідний. Якщо  , то коефіцієнт кореляції не вірогідний. Вірогідність кореляційного відношення визначають аналогічно.
, то коефіцієнт кореляції не вірогідний. Вірогідність кореляційного відношення визначають аналогічно.


