

Мы поможем в написании ваших работ!
ЗНАЕТЕ ЛИ ВЫ?
|
Волновая оптика. Световая волна и ее основные свойства. Абсолютный показатель преломления и его связь с диэлектрической проницаемостью среды. Волновой вектор. Длина и частота волны, связь между ними.
Похожие статьи вашей тематики
Оптика – раздел физики в котором изучается природа света, законы его распространения и взаимодействия с веществами.
Фазовая скорость распространения волны в вакууме:

Абсолютный показатель преломления среды, связывает эл. магн. и оптические свойства вещества:

Для большинства прозрачных сред 
Значение n характеризует оптическую плотность среды: чем больше n, тем оптически более плотной является среда.
Известно, что физиологическое, фотохимическое, фотоэлектрическое и другие действия вызваны именно электрической составляющей эл. магн. поля. Поэтому вектор направления  электрической составляющей эл. магн. волны называется световым вектором, амплитуду которого часто обозначают электрической составляющей эл. магн. волны называется световым вектором, амплитуду которого часто обозначают  . .

Фаза волны:

Волновая поверхность – поверхность, в каждой точке которой колебания вектора  и вектора ( и вектора ( ) происходят в одинаковой фазе. ) происходят в одинаковой фазе.
В случае плоской волны волновой поверхностью является плоскость перпендикулярная направлению распространения волны, по которому направлен волновой вектор  . .
Волновое число k – модуль волнового вектора равно:

где ω – циклическая частота; υ – фазовая скорость волны; λ – расстояние, которое проходит фронт волны за период T.

λ – расстояние между двумя точками среды, разность фаз колебаний которых равна 2π:

Основные свойства световой волны:
- Эл. магн. волны является поперечной
-  , ,  , ,  – правовинтовая система; – правовинтовая система;
- Векторы  и и  изменяются синфазно; изменяются синфазно;
- 
- При переходе световой волны из вакуума в прозрачную среду с показателем преломления n:
а) частота не изменяется
б) длина волны изм в n раз
 47. Принцип Ферма. Оптическая длина пути. Таутохронность геометрических путей. Законы геометрической оптики 47. Принцип Ферма. Оптическая длина пути. Таутохронность геометрических путей. Законы геометрической оптики
Принцип Ферма в геометрической оптике — постулат, предписывающий лучу света двигаться из начальной точки в конечную точку по пути, минимизирующему время движения. В более точной формулировке: свет выбирает один путь из множества близлежащих, требующих почти одинакового времени для прохождения; другими словами, любое малое изменение этого пути не приводит в первом порядке к изменению времени прохождения.
Оптическая длина пути между двумя точками среды — расстояние, на которое свет распространился бы в вакууме за время его прохождения между этими точками.
Таутохронные пути между двумя точками – пути, требующие для своего прохождения световыми лучами одинакового времени.
В основе геометрической оптики лежат несколько простых эмпирических законов:
1. Закон прямолинейного распространения света(Принцип Ферма)
2. Закон независимого распространения лучей
3. Закон отражения света
4. Закон преломления света
5. Закон обратимости светового луча.
Закон независимого распространения лучей — второй закон геометрической оптики, который утверждает, что световые лучи распространяются независимо друг от друга.
Отражение — физический процесс взаимодействия волн или частиц с поверхностью, изменение направления волнового фронта на границе двух сред с разными свойствами, в котором волновой фронт возвращается в среду, из которой он пришёл. Одновременно с отражением волн на границе раздела сред, как правило, происходит преломление волн.
Закон обратимости светового луча. Согласно ему, луч света, распространившийся по определённой траектории в одном направлении, повторит свой ход в точности при распространении и в обратном направлении.
48.Световая волна на границе раздела двух однородных изотропных прозрачных диэлектриков при ее нормальном падении на границу. Коэффициенты отражения и пропускания.
Соотношения между световыми векторами падающей  1, отражённой 1, отражённой  ’1 и преломлённой ’1 и преломлённой  волнами: волнами:
 ; ; 
из которых следует:
-  ,то колеб-ия свет. вект. падающей и преломл-ой волны происх. cинфазно; ,то колеб-ия свет. вект. падающей и преломл-ой волны происх. cинфазно;
-  т.е. колеб-ия свет. вект. падающей и отраж-ой – синфазно; т.е. колеб-ия свет. вект. падающей и отраж-ой – синфазно;
-  т.е. колеб-ия свет. вект. падающей и отраж-ой – противофазно; т.е. колеб-ия свет. вект. падающей и отраж-ой – противофазно;
При отражении от оптич. более плотной среды ее фаза скачком меняется на противоположную.
Коэффициент отражения:
 где I’1 и I’ — интенсивности отражённой и падающих волн. где I’1 и I’ — интенсивности отражённой и падающих волн.
Коэффициент пропускания:
 где I2 и I’ — интенсивности преломлённой и падающих волн. где I2 и I’ — интенсивности преломлённой и падающих волн.
 При отсутствии поглощения: R+D=1 При отсутствии поглощения: R+D=1
При нормальном падении световой волны на границу разделу двух n1=1, n2=1,5 при расчётах коэффициент отражения R=0.04.
Одним из наиболее распространённых способов уменьшить интенсивность отражения света является просветление оптики, в основе которой лежит интерференция света.
49.Интерференция световых волн. Среднее по времени значение интенсивности результирующего света в точке наблюдения. Понятие о когерентности.
Интер-ция – это явл-ние перерспред-ия в пространстве свет. энергии с образ-нием усойчивой во времени картины чередующихся макс-ов и миним-ов интерфен.ого света, при наложении двух и нескольких световых волн.
Средняя интенсивность результирующего света в точке наблюдения:
 где I1 и I2 – интенсивности двух световых накладываемых волн. где I1 и I2 – интенсивности двух световых накладываемых волн.
Cледует, что I интенсивность света в любой т. простр-ва зависит от Ф2-Ф1.
1. Если, колебания двух световых волн не согласованы друг с другом (их Ф2-Ф1 – изменяется со временем), то такие колеб-ия (и волны) – некогерентные.
 — средняя интенсивность двух некогерентных волн. — средняя интенсивность двух некогерентных волн.
2. Если, Ф2-Ф1=const, то такие волны – когерентные.
 Ф2-Ф1) - ср. интенс-ость двух коге-ных волн. Ф2-Ф1) - ср. интенс-ость двух коге-ных волн.
- если cos(Ф2-Ф1) > 0, то I > I1+I2 – усиление света.
- если cos(Ф2-Ф1) < 0, то I < I1+I2 – ослабление света.
Т.е. при наложении двух когерентных волн происходит чередование максимумов и минимумов, не зависящих от времени.
50.Оптическая разность хода двух когерентных волн и ее связь с разностью фаз этих волн. Условие возникновения интерференционных максимумов и минимумов.
Фаза световых волн:

L= n*r (где r – геометр. путь, n – показатель преломления),  –длина волны в вакууме. –длина волны в вакууме.
 где где  =1 или 0. =1 или 0.
1)  , если общее число отражений первой и второй волны от оптически более плотной среды на L1 и L2 является числом нечетным. , если общее число отражений первой и второй волны от оптически более плотной среды на L1 и L2 является числом нечетным.
2)  во всех остальных случаях. во всех остальных случаях.
Δ =  — оптическая разность хода. — оптическая разность хода.
Тогда, разность фаз можно выразить:
 Условие образования интерференционного max-ума Условие образования интерференционного max-ума
Если cos(Ф2 - Ф1) = 1, то средняя интенсивность max-ума:
 Тогда разность фаз: Тогда разность фаз:  , т.е колебания происходят в одной фазе. , т.е колебания происходят в одной фазе.
Тогда оптическая разность хода Δ должна быть равна чётному числу полудлин:
 Если в нек. т. пространства две когерентные волны возбуждают колебания с одинаковыми фазами или опт. разность хода этих волн равна чётному числу полудлин волн в вакууме, то в этой т. наблюдается интерференционный максимум. Если в нек. т. пространства две когерентные волны возбуждают колебания с одинаковыми фазами или опт. разность хода этих волн равна чётному числу полудлин волн в вакууме, то в этой т. наблюдается интерференционный максимум.
Условие образование интерференционного min-ума
Если cos(Ф2 - Ф1) = -1, то средняя интенсивность min-ума:
 Тогда разность фаз: Тогда разность фаз:  , т.е колебания происходят в одной фазе. , т.е колебания происходят в одной фазе.
Тогда оптическая разность хода Δ должна быть равна чётному числу полудлин:
 Если в нек. т. пространства две когерентные волны возбуждают колебания с противоположными фазами или опт. разность хода этих волн равна нечётному числу полудлин волн в вакууме, то в этой т. наблюдается интерференционный минимум. Если в нек. т. пространства две когерентные волны возбуждают колебания с противоположными фазами или опт. разность хода этих волн равна нечётному числу полудлин волн в вакууме, то в этой т. наблюдается интерференционный минимум.
Для получения устойчивого интерференционную картину от обычного источника света, разделить их на две когерентные между собой волны, затем их свести в области пространства, где должна наблюдаться интерференция, так чтобы оптические пути этих волн были разные.
Все схемы получения устойчивой штриховой картины световых волн основаны на этом одном общем принципе.
51.Опыт Юнга. Координаты положений на экране интерференционных максимумов и минимумов. Ширина интерференционной полосы.
Установка состояла из одной непрозрачной диафрагмы с узкой щелью S, освещенной ярким светом, и другой непрозрачной диафрагмы с двумя узкими щелями S1 и S2. Проходя через S, свет образовывал расходящуюся волну, падающую на щели S1 и S2. Эти щели действ-ли как когерентные источники, и исход. волны перекрываясь, образовывали на экране интерференционную картину – систему черных и белых полос.
Оптическая разность хода:  , где , где  , т.к. волны падая на , т.к. волны падая на  не испытывают отражения от оптически более плотной среды. не испытывают отражения от оптически более плотной среды.
Т.к. n = 1:
1) 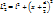 2) 2)  3) 3) 
4)  5) 5)  6) 6) 
Т.к 
7) 
8) 
откуда координаты положительных интерференционных максимумов
9)  
при m = 0  = 0 - центральный максимум; = 0 - центральный максимум;
при m = 1  = 0 - 1-й максимум; = 0 - 1-й максимум;
при m = 2  = 0 - 2-ой максимум; = 0 - 2-ой максимум;
при m = -1  = 0 - -1-й максимум; = 0 - -1-й максимум;
Теперь так же с минимумом:
10) 
координаты положительных интерференционных минимумов
11)  
Ширина интерференционной полосы  - расстояние между двумя соседними максимумами иkb минимумами. - расстояние между двумя соседними максимумами иkb минимумами.
 Измерив длину Измерив длину 
Измерит. приборы, принцип действия которых основан на явл-нии интерференции с помощью которых можно определить длину волны  , называются интерференанометрами. , называются интерференанометрами.
51.Зеркало Ллойда. Координаты положений на экране интерференционных максимумов и минимумов. Ширина интерференционной полосы.
Узкая щель S, освещена монохроматическим светом с  . Расстояние от щели до плоскости зеркала d. На параллельной ели и перпендикулярной плоскости зеркала экране, удалено на расстоянии l >> d от щели, образует светлые и темные интерференционные полосы. Ось Оx направлена верх. Свет волны, исходящий от источника S, интерферируется с волной, отраженной от поверхности зеркала. . Расстояние от щели до плоскости зеркала d. На параллельной ели и перпендикулярной плоскости зеркала экране, удалено на расстоянии l >> d от щели, образует светлые и темные интерференционные полосы. Ось Оx направлена верх. Свет волны, исходящий от источника S, интерферируется с волной, отраженной от поверхности зеркала.
Источник когерентных волн – реал. источник света S, и его мнимое изображ. S’.
Т.к. вторая волна на  испытывает в т. A отражение от оптически более плотной среды, то оптическая разность хода испытывает в т. A отражение от оптически более плотной среды, то оптическая разность хода  от когерентных источников S и S’ в точке P с координатами x равна: от когерентных источников S и S’ в точке P с координатами x равна:
 где учтено, что в воздухе где учтено, что в воздухе  и и 
Т.к n = 1, то по теореме Пифагора:
1)  2) 2)  3) 3) 
4)  5) 5)  6) 6) 
7)  — оптическая разность хода — оптическая разность хода
8) 
9) 
откуда координаты положительных интерференционных максимумов
10)  
Теперь так же с минимумом:
11) 
12) 
координаты положительных интерференционных минимумов
13)  , где m= 0, , где m= 0, 
Ширина интерференционной полосы  - расстояние между двумя соседними максимумами иkb минимумами. - расстояние между двумя соседними максимумами иkb минимумами.
 52.Интерференция света в тонкой плоскопараллельной пластине. Просветление оптики. 52.Интерференция света в тонкой плоскопараллельной пластине. Просветление оптики.
На прозрачную плоскопараллельную пластину толщиной d и показателем преломления n под углом  падает монохромат. свет. волна, длина которой падает монохромат. свет. волна, длина которой  В результате, отражаясь от верхней и нижней части пластины, падающая волна разделяется на две когерентные между собой волны. В результате, отражаясь от верхней и нижней части пластины, падающая волна разделяется на две когерентные между собой волны.
По закону преломления света:
 ,откуда ,откуда  угол преломления) угол преломления)
Исходящие от пластины лучи параллельны друг другу, поэтому наблюдение ведётся на экране, расположенном на фокальной плоскости собирающей линзы Л (или глазом).
Оптич. разность хода  в т. P, т.к и на линии DC (геометр. пути DC и PC – таутохронны). в т. P, т.к и на линии DC (геометр. пути DC и PC – таутохронны).
Поскольку в т. А отражение от более плотной среды, то:
1)  2) 2) 
3) 
4) 
Отраженный свет максимально усилен:
5)  ,тогда ,тогда
6) 
при  - минимальная толщина пластины, при которой отраженный свет будет максимально усилен. - минимальная толщина пластины, при которой отраженный свет будет максимально усилен.
Отражённый свет максимально ослаблен:
7)  ,тогда ,тогда
8) 
при  - минимальная толщина пластины, при которой отраженный свет будет максимально ослаблен. - минимальная толщина пластины, при которой отраженный свет будет максимально ослаблен.
Интерференция света при отражении от тонких пластинок лежит в основе просветления оптики – метода улучшения качества оптических приборов за счёт уменьшения коэффициента отражения поверхностей оптических деталей.
На поверхность линзы наносится тонкая плёнка с 
При отражения света от границ «воздух-плёнка» и «плёнка-стекло» возникает интерференция отражения волн.
Толщину плёнки d, показатель преломления стекла nст и показатель преломления плёнки n подбирают так, чтобы для отражения волн, выполнялось условие интерференционного минимума.
В результате светопропускание этих волн (к области с  глаз наиболее чувствителен) увеличивается. глаз наиболее чувствителен) увеличивается.
54.Кольца Ньютона. Радиусы светлых и темных колец в отраженном свете.
Интерф-ная картина «Кольцо Ньютона» наблюдается при отражении света от поверхн. тонкой клиновидной прослойки, образующ. плоской стеклянной пластинкой и соприкасающейся к ней плоск.-выпуклой линзы с большим радиусом R кривизны поверхности.
При норм. падении на поверхн. линзы света с дл. волны  в т. А луч 1* частично отражается (луч 1) и частично преломляется (луч 2), отражаясь в точке B, испытывая последующее преломление в т. С. Лучи 1 и 2 интерферированны между собой так, что малый угол между ними делает их когерентными. в т. А луч 1* частично отражается (луч 1) и частично преломляется (луч 2), отражаясь в точке B, испытывая последующее преломление в т. С. Лучи 1 и 2 интерферированны между собой так, что малый угол между ними делает их когерентными.
Геом. место точек один-ой толщины hm прослойки представляет собой окружность, поэтому интерф-ая картина имеет вид черед-хся тёмных и светлых концентрических колец с центром в т. соприкосновения линзы с пластиной.
Т.к R-велико, то точки A и C наход-ся на малом расстоянии друг от друга.
Если прослойка воздушная (n = 1), то опт-кие длины путей отража-ся от её обеих поверхностей интерф-ных лучей 1 и 2 соответственно равны:
L1 = 0 L2 = hm
где hm – толщина воздушн. прослойки, где происходят отражения волн 1 и 2
Тогда оптическая разность хода равна:
 где где 
Пот теор. Пифагора:
 где где  , то , то
 Тогда Тогда
 Светл. кольца будут наблюдаться в тех точках, для которых выполняется условие образования интерфер-ого максимума: Светл. кольца будут наблюдаться в тех точках, для которых выполняется условие образования интерфер-ого максимума:

Тогда
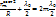 Откуда радиус светлых конец: Откуда радиус светлых конец:
 где m=1,2,… где m=1,2,…
А радиус тёмных колец:
 , где m=0,1,2,… , где m=0,1,2,…
Значение m = 0 соответственно минимум тёмного пятна, конечные размеры которого обусловлены упругой деформацией стекла.
55.Дифракция света. Принцип Гюйгенса – Френеля. Дифракция Френеля и Фраунгофера.
Дифракция света – явление перераспределения в пространстве световой энергии с возможностью образования устойчивой картины чередующихся максимумов и минимумов интенсивности света при его распространении в среде с резкой неоднородностью. В узком смысле – огибание волнами препятствий встречающихся на их пути и проникновение света в области геом. тени. Такое явление можно наблюдать при прохождении света через непрозрачные тела произвольной формы или если свет проходит через малые отверстия в непрозрачной диафрагме.
По законам геометрической оптики за ними находились бы области геометр. тени, однако из-за дифракции вместо резкой границы между светом и тенью наблюдается сложная картина интенсивности света.
В зависимости от соотношения между характерными размерами неодн. r0, расстоянием l между ней и т. наблюдения, а также длиной волны  различают: различают:
1. Дифракция Френеля – диф-ция в сход-хся пучках, когда 
2. Дифракция Фраунгофера – диф-ция в парал-ных пучках, когда 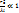
3. Если  , свет распр-яется прямолинейно – условие геом. оптики , свет распр-яется прямолинейно – условие геом. оптики
Задача теории дифракции заключается в том, чтобы при данном расположении и форме неоднородности, а также источн. света определ. раст. во всём пространстве.
Точное решение этой задачи возможно в рамках волновой теории света путём решения волнового уравнения с соотв. граничн. усл-ями на поверхности тела. В некоторых случаях оказывается достаточно приближённый метод решения дифр. задач на основе принципа Гюйгенса-Френеля.
Принцип Г-Ф
Каждый элемент dS волн. поверхности рассматривает волны являющиеся источником вторичных сфер. волн, а её амплитуда А(Р) в неко. точке Р является результатом интер-сти когерентных волн.
Аналитическое выражение П Г-Ф

  ( ( ) )
Интенсивность света пропорциональна квадрату амплитуды
 Между интерф-ией и дифракцией нет принцип. различия. Между интерф-ией и дифракцией нет принцип. различия.
Исторически интерференция называла суперпозиции от конечного числа дискретных когерентных источников, а дифракция – от непрерывно расположенных когерентных источников.
56.Дифракция Френеля на круглом отверстии. Метод зон Френеля.
В случае обладания симметрии, нахождение амплитуды A(P) результ. колеб-ния в т. Р интегрирование можно заменить вычислением дискретной суммы.
МЕТОД ЗОН ФРЕНЕЛЯ
Волновая поверхность разбивается на участки – зоны Френеля – т.к. что расстояние от краёв соседних до т. Р отличается на  . .
При этом колеб-ия свет.вектора, возбуждаемого в т. Р вторичными источниками, расположенных в двух соседних зонах, будут отличаться на  по фазе. по фазе.
Амплитуда результирующих колебаний:
 m – число зон Френеля m – число зон Френеля
“+”- соотв. нечётным значениям i и m;
“-”- соотв. чётным значениям i и m
Площадь i- ой зоны:
 Следует, что площадь всех зон одинаковы при достаточно малых i. Следует, что площадь всех зон одинаковы при достаточно малых i.
Амплитуда результирующих колебаний светового вектора, возбуждаемых в т. Р всеми открытыми отверстиями зон общим числом m:
 Общее число зон Френеля: Общее число зон Френеля:
 Т.к. (I=A2), то интенсивность в т. Р при: Т.к. (I=A2), то интенсивность в т. Р при:



 Дифракционная картина – тёмные и светлые кольца. Дифракционная картина – тёмные и светлые кольца.
В отсутствии диафрагмы амплитуда равна:
 Т.к. площадь половины первой зоны очень мала, то можно считать, что свет распространяется прямолинейно. Т.к. площадь половины первой зоны очень мала, то можно считать, что свет распространяется прямолинейно.
Данное является доказательством прямолинейного распространения света в однородной среде, основанного на принципе Г-Ф.
Теория дифракции (и интерференции) применима к волнам любой физической волны.
57. Дифракция Фраунгофера на щели. Угловое распределение интенсивности света в дифракционной картине. Условие положений дифракционных минимумов.
ДФ – это дифракция света в параллельных пучках, которые в рамках волновой теории моделируется с помощью плоских волн.
Амплитуда результирующих колебаний светового вектора в т.Р 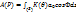
Фаза колебаний:
 Таким образом амплитуда равна: Таким образом амплитуда равна:
 а угловое распределение интенсивности: а угловое распределение интенсивности:
 1) при 1) при  в центре расположен дифракционный максимум, в котором интенсивность света наибольшая. в центре расположен дифракционный максимум, в котором интенсивность света наибольшая.
2)  ) = 0 при ) = 0 при
 и в итоге условие условных положений минимумов в дифракционной картине: и в итоге условие условных положений минимумов в дифракционной картине:
 Для определения положения максимумов: Для определения положения максимумов:
58.Дифракционная решетка. Угловое распределение интенсивности света в дифракционной картине. Условие положений главных максимумов, главных и промежуточных минимумов. Угловая дисперсия и разрешающая способность.
Дифр-ая решётка – спектральный прибор, состоящий из большого числа регулярно расположенных щелей.
Период d дифр-ой решётки – расстояние между двумя серединами щелей.
d=a+b, где a – ширина непрох-ого участка; b – ширина щели.
Угловое распределение интенсивности света в дифрак-ой картине:
 1) I максимальна при 1) I максимальна при  и и
Условие угловых положений главных максимумов(урав-ие дифр-ной решётки):
 2) I минимальна при: 2) I минимальна при:
 Условие угловых положений главных минимумов: Условие угловых положений главных минимумов:
 Условие угловых положений добавочных минимумов: Условие угловых положений добавочных минимумов:
 При большом числе N щелей интен-ость добав-ных макс-умов практ-и равна нулю. При большом числе N щелей интен-ость добав-ных макс-умов практ-и равна нулю.
Угловая дисперсия D – характеризует степень углового разделения волн с разделёнными длинами:

 Чем меньше период d решётки и чем выше порядок спектра m, тем больше её угловая дисперсия. Чем меньше период d решётки и чем выше порядок спектра m, тем больше её угловая дисперсия.
Разрешающая способность R:
 где где  – минимальная разность длин волн, соответствующих двум спектральным линиям, при которой эти линии воспринимаются раздельно, т.е. разрешающе. – минимальная разность длин волн, соответствующих двум спектральным линиям, при которой эти линии воспринимаются раздельно, т.е. разрешающе.
Для дифр-ой решётки  с помощью критерия Релея, согласно которому, если две одинаковые интенсивности I1 спектральных линий, соответств. с помощью критерия Релея, согласно которому, если две одинаковые интенсивности I1 спектральных линий, соответств.  , разрешающие, если максимум одной линии совпадает с минимумом другой. , разрешающие, если максимум одной линии совпадает с минимумом другой.
При этом в промежутке между максимумами результирующая интенсивность I составляет 80% от I1.
Разрешающая способность дифр-ной решётки:
 59.Поляризация света. Естественный и поляризованный свет. Закон Малюса. 59.Поляризация света. Естественный и поляризованный свет. Закон Малюса.
Свет обычного источника является результатом изменения его атомами независимо друг от друга огромного числа цугов волн (кратковременный световой импульс τ~10-8 ), в каждом из которых направление колебаний светового вектора ориентированно случайным образом.
То есть в результате световые волны колебания вектора Е происходит вдоль всевозможных равномерных направлений, перпендикулярно направлениям распространения света(вект k).
Если в каждой точке поля световой волны вектор Е совершает колебания, которые быстро и беспорядочно изменяются в плоскости, перпендикулярно направлены распространению света (вект k), то свет – естественный.
Поляризованный свет – светоавя волна в которой направление колебательного вектора Е, упорядочена некоторым образом, либо направление колебаний вектора Е в каждо точке просто остается неизменным, либо ищменяется по определенному закону.
Если в каждой точке поля световой волны вектор Е совершает колебания, изменяющиеся только в одной плоскости, содержащей вектор, то свет – линейно поляризованный.
Плоскость поляризации – плоскость, содержащая векторы E и k.
Кроме линейного разложения есть эллиптическое и круговое.
Если в каждой точек поле световой волны вектор Е изменяестся со временем так, что в плоскости, перпендикулярной направления распространения вдоль конца вектора описывает эллипс, то свет эллиптически поляризован; Окружность – циркулярно поляризован.
Частично поляризованным называется свет, если в нем имеется преимущественно направленный вектор Е.
Частично поляризованный свет можно рассмотреть как совокупность одновременно распространяющихся в одном и том же направлении естественного и линейно поляризованного света.
Поляризация света может возникнуть при различных физических процессах:
1. отражение и преломление света на границе раздела двух изотропных сред
2. прохождение света при прохождении через анизотропическую среду
3. рассеивание света и др.
Поляризатор – оптическое устройство для получения полностью или частичн поляризованного света.
Линейный поляризатор пропускает тольлко ту часть падающей на него световой волны, в которой направление колебания вектора Е параллельно некоторой плоскости, называения плоскостью пропускания ПП.
При этом остаточная часть световой волны задерживается полностью или частично.
Анализатор – поляризатор с помощью которого исследуется поляризация света.
Линейный свет падает на поляризатор, плоскость пропускания которого составляет с направлением колебания вектора Е0 угол ф.
Векторы А0 и А - Амплитуды светового вектора соответственно падающего на поляризатор и прошедшего через него света, модули которых связаны равенством:
 Так как поляризатор пропускает только ту составляющую А0 которая параллелтна плоскости пропускания. Так как поляризатор пропускает только ту составляющую А0 которая параллелтна плоскости пропускания.
Поэтому I~A2, то
 - Закон Малюса - Закон Малюса
I0 – интенсивность падающего света.
I – интенсивность света прошедшего через поляризатор.
Если на поляризатор падает естественно равнов., то среднее значение квадрата косинуса от 0 до 2π
 Тогда по закону Малюса интенсивность I прошедшего света через поляризатор: Тогда по закону Малюса интенсивность I прошедшего света через поляризатор:
 60.Степень поляризации частично поляризованного света. Поляризация света при его отражении и преломлении. Закон Брюстера. 60.Степень поляризации частично поляризованного света. Поляризация света при его отражении и преломлении. Закон Брюстера.
Частично поляризацию света можно представить в виде наложения двух некогерентных линейно … волн с взаимно перпендикулярными плоскостями поляризации.
При этом взаимно перпендикулярные составляющие света имеют различные интенсивности.
Частичная поляризация света характеризуется степенью поляризации P:

где  и и  – максимальная и минимальная интенсивности частично поляризованного света, соответствующие двум взаимно перпендикулярным составляющим вектора – максимальная и минимальная интенсивности частично поляризованного света, соответствующие двум взаимно перпендикулярным составляющим вектора  . .
Для естественного света  поэтому P = 0; поэтому P = 0;
Для линейно поляризованного света  поэтому P = 1; поэтому P = 1;
Для частичной поляризации  поэтому 0 < P < 1; поэтому 0 < P < 1;
Возможность получения линейно поляризованного света при его отражении и преломлении на границе раздела двух изотропных однородных прозрачных диэлектриков следует из формул Френеля, которые определяют соотношение между амплитудами падающей, отраженной и преломленной световых волн.
Амплитуду светового вектора разложим на два вектора, один из которых лежит в плоскости падения (ǁ), а другой – перпендикулярно этой плоскости (⊥):

где  вектор перпендикулярный плоскости падения; вектор перпендикулярный плоскости падения;

 – волновой вектор падающей волны; – волновой вектор падающей волны;
Для отраженной волны:


Для преломленной волны:


Формулы Френеля:




Из формул следует, что при падении на границу раздела естественного света  под под  преломление и отражение света оказываются частично поляризованными: в преломлении преобладают колебания светового вектора параллельного плоскости падения преломление и отражение света оказываются частично поляризованными: в преломлении преобладают колебания светового вектора параллельного плоскости падения  , а в отражении – перпендикулярного ей , а в отражении – перпендикулярного ей  . .
Степень поляризации преломления и отражения зависит от угла α.
Т.к.  ,то ,то 
т.к.  , т.е. отраженный свет будет полностью поляризован в плоскости, перпендикулярной плоскости падения. При этом степень поляризации P преломленного света максимально, но P < 1. , т.е. отраженный свет будет полностью поляризован в плоскости, перпендикулярной плоскости падения. При этом степень поляризации P преломленного света максимально, но P < 1.
Угол паления  , при котором отраженный свет полностью поляризуется, называется углом Брюстера. , при котором отраженный свет полностью поляризуется, называется углом Брюстера.
Закон Брюстера:

|






 электрической составляющей эл. магн. волны называется световым вектором, амплитуду которого часто обозначают
электрической составляющей эл. магн. волны называется световым вектором, амплитуду которого часто обозначают  .
.

 ) происходят в одинаковой фазе.
) происходят в одинаковой фазе. .
.



 47. Принцип Ферма. Оптическая длина пути. Таутохронность геометрических путей. Законы геометрической оптики
47. Принцип Ферма. Оптическая длина пути. Таутохронность геометрических путей. Законы геометрической оптики 1, отражённой
1, отражённой  волнами:
волнами: ;
; 
 ,то колеб-ия свет. вект. падающей и преломл-ой волны происх. cинфазно;
,то колеб-ия свет. вект. падающей и преломл-ой волны происх. cинфазно;  т.е. колеб-ия свет. вект. падающей и отраж-ой – синфазно;
т.е. колеб-ия свет. вект. падающей и отраж-ой – синфазно; где I’1 и I’ — интенсивности отражённой и падающих волн.
где I’1 и I’ — интенсивности отражённой и падающих волн. где I2 и I’ — интенсивности преломлённой и падающих волн.
где I2 и I’ — интенсивности преломлённой и падающих волн. При отсутствии поглощения: R+D=1
При отсутствии поглощения: R+D=1 где I1 и I2 – интенсивности двух световых накладываемых волн.
где I1 и I2 – интенсивности двух световых накладываемых волн. — средняя интенсивность двух некогерентных волн.
— средняя интенсивность двух некогерентных волн. Ф2-Ф1) - ср. интенс-ость двух коге-ных волн.
Ф2-Ф1) - ср. интенс-ость двух коге-ных волн.
 –длина волны в вакууме.
–длина волны в вакууме. где
где  =1 или 0.
=1 или 0.  , если общее число отражений первой и второй волны от оптически более плотной среды на L1 и L2 является числом нечетным.
, если общее число отражений первой и второй волны от оптически более плотной среды на L1 и L2 является числом нечетным. во всех остальных случаях.
во всех остальных случаях. — оптическая разность хода.
— оптическая разность хода. Условие образования интерференционного max-ума
Условие образования интерференционного max-ума Тогда разность фаз:
Тогда разность фаз:  , т.е колебания происходят в одной фазе.
, т.е колебания происходят в одной фазе. Если в нек. т. пространства две когерентные волны возбуждают колебания с одинаковыми фазами или опт. разность хода этих волн равна чётному числу полудлин волн в вакууме, то в этой т. наблюдается интерференционный максимум.
Если в нек. т. пространства две когерентные волны возбуждают колебания с одинаковыми фазами или опт. разность хода этих волн равна чётному числу полудлин волн в вакууме, то в этой т. наблюдается интерференционный максимум. Тогда разность фаз:
Тогда разность фаз:  , т.е колебания происходят в одной фазе.
, т.е колебания происходят в одной фазе. Если в нек. т. пространства две когерентные волны возбуждают колебания с противоположными фазами или опт. разность хода этих волн равна нечётному числу полудлин волн в вакууме, то в этой т. наблюдается интерференционный минимум.
Если в нек. т. пространства две когерентные волны возбуждают колебания с противоположными фазами или опт. разность хода этих волн равна нечётному числу полудлин волн в вакууме, то в этой т. наблюдается интерференционный минимум. , где
, где  не испытывают отражения от оптически более плотной среды.
не испытывают отражения от оптически более плотной среды.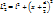 2)
2)  3)
3) 
 5)
5)  6)
6) 





 = 0 - центральный максимум;
= 0 - центральный максимум; = 0 - 1-й максимум;
= 0 - 1-й максимум; = 0 - 2-ой максимум;
= 0 - 2-ой максимум; = 0 - -1-й максимум;
= 0 - -1-й максимум;

 - расстояние между двумя соседними максимумами иkb минимумами.
- расстояние между двумя соседними максимумами иkb минимумами. Измерив длину
Измерив длину 
 , называются интерференанометрами.
, называются интерференанометрами. . Расстояние от щели до плоскости зеркала d. На параллельной ели и перпендикулярной плоскости зеркала экране, удалено на расстоянии l >> d от щели, образует светлые и темные интерференционные полосы. Ось Оx направлена верх. Свет волны, исходящий от источника S, интерферируется с волной, отраженной от поверхности зеркала.
. Расстояние от щели до плоскости зеркала d. На параллельной ели и перпендикулярной плоскости зеркала экране, удалено на расстоянии l >> d от щели, образует светлые и темные интерференционные полосы. Ось Оx направлена верх. Свет волны, исходящий от источника S, интерферируется с волной, отраженной от поверхности зеркала. испытывает в т. A отражение от оптически более плотной среды, то оптическая разность хода
испытывает в т. A отражение от оптически более плотной среды, то оптическая разность хода  от когерентных источников S и S’ в точке P с координатами x равна:
от когерентных источников S и S’ в точке P с координатами x равна: где учтено, что в воздухе
где учтено, что в воздухе  и
и  2)
2)  3)
3) 
 5)
5)  6)
6) 
 — оптическая разность хода
— оптическая разность хода 


 , где m= 0,
, где m= 0, 
 52.Интерференция света в тонкой плоскопараллельной пластине. Просветление оптики.
52.Интерференция света в тонкой плоскопараллельной пластине. Просветление оптики.  падает монохромат. свет. волна, длина которой
падает монохромат. свет. волна, длина которой  В результате, отражаясь от верхней и нижней части пластины, падающая волна разделяется на две когерентные между собой волны.
В результате, отражаясь от верхней и нижней части пластины, падающая волна разделяется на две когерентные между собой волны. ,откуда
,откуда  угол преломления)
угол преломления)


 ,тогда
,тогда
 - минимальная толщина пластины, при которой отраженный свет будет максимально усилен.
- минимальная толщина пластины, при которой отраженный свет будет максимально усилен.  ,тогда
,тогда
 - минимальная толщина пластины, при которой отраженный свет будет максимально ослаблен.
- минимальная толщина пластины, при которой отраженный свет будет максимально ослаблен.
 глаз наиболее чувствителен) увеличивается.
глаз наиболее чувствителен) увеличивается. где
где 
 где
где  , то
, то  Тогда
Тогда  Светл. кольца будут наблюдаться в тех точках, для которых выполняется условие образования интерфер-ого максимума:
Светл. кольца будут наблюдаться в тех точках, для которых выполняется условие образования интерфер-ого максимума:
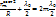 Откуда радиус светлых конец:
Откуда радиус светлых конец: где m=1,2,…
где m=1,2,… , где m=0,1,2,…
, где m=0,1,2,…
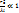
 , свет распр-яется прямолинейно – условие геом. оптики
, свет распр-яется прямолинейно – условие геом. оптики

 (
( )
) Между интерф-ией и дифракцией нет принцип. различия.
Между интерф-ией и дифракцией нет принцип. различия. .
. по фазе.
по фазе.  m – число зон Френеля
m – число зон Френеля Следует, что площадь всех зон одинаковы при достаточно малых i.
Следует, что площадь всех зон одинаковы при достаточно малых i. Общее число зон Френеля:
Общее число зон Френеля: Т.к. (I=A2), то интенсивность в т. Р при:
Т.к. (I=A2), то интенсивность в т. Р при:


 Дифракционная картина – тёмные и светлые кольца.
Дифракционная картина – тёмные и светлые кольца. Т.к. площадь половины первой зоны очень мала, то можно считать, что свет распространяется прямолинейно.
Т.к. площадь половины первой зоны очень мала, то можно считать, что свет распространяется прямолинейно.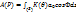
 Таким образом амплитуда равна:
Таким образом амплитуда равна: а угловое распределение интенсивности:
а угловое распределение интенсивности: 1) при
1) при  в центре расположен дифракционный максимум, в котором интенсивность света наибольшая.
в центре расположен дифракционный максимум, в котором интенсивность света наибольшая. ) = 0 при
) = 0 при и в итоге условие условных положений минимумов в дифракционной картине:
и в итоге условие условных положений минимумов в дифракционной картине: Для определения положения максимумов:
Для определения положения максимумов:  1) I максимальна при
1) I максимальна при  и
и 2) I минимальна при:
2) I минимальна при: Условие угловых положений главных минимумов:
Условие угловых положений главных минимумов: Условие угловых положений добавочных минимумов:
Условие угловых положений добавочных минимумов: При большом числе N щелей интен-ость добав-ных макс-умов практ-и равна нулю.
При большом числе N щелей интен-ость добав-ных макс-умов практ-и равна нулю.
 Чем меньше период d решётки и чем выше порядок спектра m, тем больше её угловая дисперсия.
Чем меньше период d решётки и чем выше порядок спектра m, тем больше её угловая дисперсия. где
где  – минимальная разность длин волн, соответствующих двум спектральным линиям, при которой эти линии воспринимаются раздельно, т.е. разрешающе.
– минимальная разность длин волн, соответствующих двум спектральным линиям, при которой эти линии воспринимаются раздельно, т.е. разрешающе. , разрешающие, если максимум одной линии совпадает с минимумом другой.
, разрешающие, если максимум одной линии совпадает с минимумом другой. 59.Поляризация света. Естественный и поляризованный свет. Закон Малюса.
59.Поляризация света. Естественный и поляризованный свет. Закон Малюса. Так как поляризатор пропускает только ту составляющую А0 которая параллелтна плоскости пропускания.
Так как поляризатор пропускает только ту составляющую А0 которая параллелтна плоскости пропускания. - Закон Малюса
- Закон Малюса Тогда по закону Малюса интенсивность I прошедшего света через поляризатор:
Тогда по закону Малюса интенсивность I прошедшего света через поляризатор: 60.Степень поляризации частично поляризованного света. Поляризация света при его отражении и преломлении. Закон Брюстера.
60.Степень поляризации частично поляризованного света. Поляризация света при его отражении и преломлении. Закон Брюстера.
 и
и  – максимальная и минимальная интенсивности частично поляризованного света, соответствующие двум взаимно перпендикулярным составляющим вектора
– максимальная и минимальная интенсивности частично поляризованного света, соответствующие двум взаимно перпендикулярным составляющим вектора  поэтому P = 0;
поэтому P = 0; поэтому P = 1;
поэтому P = 1; поэтому 0 < P < 1;
поэтому 0 < P < 1;
 вектор перпендикулярный плоскости падения;
вектор перпендикулярный плоскости падения;








 под
под  преломление и отражение света оказываются частично поляризованными: в преломлении преобладают колебания светового вектора параллельного плоскости падения
преломление и отражение света оказываются частично поляризованными: в преломлении преобладают колебания светового вектора параллельного плоскости падения  , а в отражении – перпендикулярного ей
, а в отражении – перпендикулярного ей  .
. ,то
,то 
 , т.е. отраженный свет будет полностью поляризован в плоскости, перпендикулярной плоскости падения. При этом степень поляризации P преломленного света максимально, но P < 1.
, т.е. отраженный свет будет полностью поляризован в плоскости, перпендикулярной плоскости падения. При этом степень поляризации P преломленного света максимально, но P < 1. , при котором отраженный свет полностью поляризуется, называется углом Брюстера.
, при котором отраженный свет полностью поляризуется, называется углом Брюстера.



