
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение показателя преломления стеклянной плоскопараллельной пластинки при помощи микроскопаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Определение показателя преломления стеклянной плоскопараллельной пластинки при помощи микроскопа Теоретическое обоснование работы
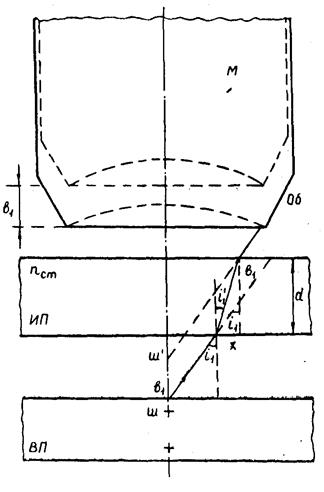
Тубус микроскопа может перемещаться в вертикальном направлении, и значения этого перемещения могут отсчитываться. Из рис. 1.2 видно, что штрих ш сетки Горяева при наблюдении в микроскоп будет виден в положении ш', смещенном от плоскости сетки Горяева на величину b1 вверх. При этом справедливы соотношения
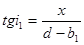 , откуда , откуда
Для определения значения d, входящего в формулу (1.1), микроскоп фокусируют на царапину ц1, нанесенную на нижнюю поверхность пластины ИП, а затем на царапину ц2, нанесенную на верхнюю поверхность пластины ИП (рис. 1.1).
где В этой работе допустима замена отношений тангенсов углов отношениями синусов, что вызывает относительную погрешность результата, не превышающую 2%. Поэтому выражение (1.1) можно переписать

откуда
Выражение (1.2) можно переписать
откуда
Подставляя значение d из выражения (1.4) в (1.3), получаем
Значения b1 и b2 измеряются по вертикальной шкале микроскопа при его перемещениях для фокусировки на резкое видение штриха сетки Горяева и царапин, нанесенных на пластину ИП.
Порядок выполнения работы
Контрольные вопросы 1. Закон преломления и физический смысл показателя преломления. 2. Нормальная и аномальная дисперсия вещества. 3. Групповая и фазовая скорость распространения света. 4. Ход лучей в микроскопе и его увеличение.
Рекомендуемая литература 1. Савельев И.В. Курс общей физики. Изд. 2-е. Т. 3, гл.I, II, VII. М., Наука, 1967. Изд. 4-е, кн. 4, гл. 3,6. М., «Наука - Физматлит», 1998г. 2. Фриш С. Э., Тиморева А. В. Курс общей физики. Т. 3. главы XXII, XXIV, XXVIII. М., Физматгиз, 1962 Лабораторная работа №3 Исследование микроскопа Содержание работы заключается в определении видимого увеличения микроскопа, линейного увеличения объектива, видимого увеличения окуляра, числовой апертуры объектива.
Порядок выполнения работы II. Определение линейного увеличения объектива 1. Надеть винтовой окуляр-микрометр. 2. С помощью винтового окуляр-микрометра измерить размер изображения стороны сетки Горяева (b) (не менее 5 раз). Результаты измерений занести в табл. 3.2. (инструкция по использованию винтового окуляр-микрометра- на рабочем столе) 3. Сетку Горяева и винтовой окуляр- микрометр снять. Результаты измерений занести в табл. 3.2. Вычислить погрешность в определении значения Таблица 3.2
Описание установки На столик измерительного микроскопа помешается стеклянная пластинка р, на которой при помощи специальной оправы с зажимами укреплена линза L. (рис. 8.2). Над линзой помещена стеклянная пластинка О, которая располагается под углом 45° к горизонтальной поверхности пластинки р. Пластинка О освещается
В работе используется измерительный микроскоп МИР-12. Микроскоп фокусируется на поверхность пластинки р. В поле зрения будут видны кольца Ньютона в отраженном свете. Измерение радиусов колец производится перемещением тубуса микроскопа в горизонтальной плоскости при помощи
Порядок выполнения работы
1. Включить лампу. Изменяя наклон пластинки О, добиться равномерного освещения поля зрения. 2. Перемещением глазной линзы окуляра сфокусировать его на четкую видимость нитей. 3. Вращением объектива в тубусе микроскопа получить четкое изображение колец Ньютона. 4. Подготовить две таблицы для записи наблюдений и вычислений. Таблица 8.1.
Здесь N1, N2 - отсчеты по микроскопу для k -го кольца слева и справа от центра; d = N2 - N1 - диаметр k -го кольца; r = 5. Вращая барабан микрометрического винта, следует подводить нить на середину пятнадцатого темного кольца и, двигаясь в одном направлении, записывать отсчеты N1 по микроскопу и номера колец в таблицу. Вращать барабан нужно только в одном направлении, иначе возникнут грубые ошибки за счет люфта винта каретки микроскопа. Перейдя центральное пятно, продолжать измерять положения середины колец и записывать в таблицу отсчеты N2 по микроскопу до пятнадцатого кольца. 6. Заменив зеленый светофильтр на красный, произвести аналогичные измерения и результаты занести в таблицу 8.2, идентичную таблице 8.1.
Подготовка к измерениям
Труба фотоэлемента должна быть закрыта крышкой. Снимать крышку следует только на время снятия отсчета. Электрическая схема (рис, 13.3) собрана. Перед началом работы следует проверить правильно ли подключены все элементы схемы. По окончании измерений схему не разбирать, следует только отключить приборы от сети.
Измерения Определение коэффициента отражения для света, поляризованного в плоскости падения rs = rs(i) в функции от угла падения i. На оправе поляризатора нанесен красный штрих. Повернуть оправу поляризатора до совмещения с индексом на трубе коллиматора. В этом положении поляризатора Р луч, выходящий из коллиматора, будет поляризован в плоскости падения на стеклянную пластинку. а) Измерение падающего светового потока F0 Снять внутренний лимб с пластиной. Повернуть трубу Т и расположить ее по направлению распространения лучей света (зайчик совместить с центром крышки трубы фотоэлемента). Снять крышку трубы фотоэлемента и снять показание милливольтметра. Сила тока в цепи селенового фотоэлемента пропорциональна падающему на него световому потоку соответственно падению напряжения U на сопротивлении милливольтметра
F0 =αU0
α - коэффициент пропорциональности; U 0 - показание милливольтметра. б) Определение коэффициента отражения rs = rs(i). Не изменяя диаметра отверстия диафрагмы коллиматора (чтобы поддерживать величину падающего светового потока постоянным), поместить внутренний лимб со стеклянной пластинкой на столик гониометра и повернуть лимб до совмещения красных индексов обоих лимбов. Это положение соответствует нормальному падению лучей на пластинку. Измерение отраженного светового потока начинать с угла падения 10°. Повернуть внутренний лимб с пластиной на угол 10°, указатель трубы фотоэлемента совместить с делением 20° (отраженный зайчик совпадает с центром крышки трубы фотоэлемента). Снять крышку трубы фотоэлемента и записать показания милливольтметра U 1. Закрыть крышку. Отраженный световой поток при данном угле падения будет равен
F 1= α U 1,
где U 1 - показание милливольтметра, α - коэффициент пропорциональности. Измерения отраженного светового потока произвести для углов падения, указанных в табл. 13.1. Результаты занести в эту таблицу. Коэффициент отражения rs для каждого угла падения определяется как отношение
rs =F1 /F0 = α U 1 / α U 0 = U 1 / U 0. Вычисленные значения rs записать в табл. 13.1. Таблица 13.1
Определение коэффициента отражения для света, поляризованного в плоскости, перпендикулярной плоскости падения rp = rp(i) На оправе поляризатора нанесен красный штрих с точкой. Повернуть оправу поляризатора до совмещения индекса на трубе коллиматора. В этом положении луч выходящий из коллиматора, будет поляризован в плоскости перпендикулярной плоскости падения. Измерения и расчет коэффициента отражения rp производят таким же способом, что и для случая света, поляризованного в плоскости падения. Результаты занести в табл. 13.2.
Таблица 13.2
Закон Малюса При вращении анализатора в своей плоскости, когда направление его пропускания перпендикулярно направлению колебаний в линейно-поляризованном луче (анализатор скрещен с поляризатором), за анализатором темно. Максимальная интенсивность за анализатором имеет место, когда направление пропускания анализатора совпадает с направлением колебаний в поляризованном луче.
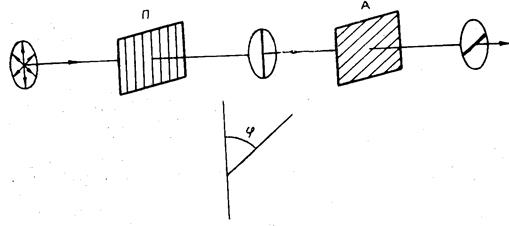
Зависимость интенсивности вышедшего из анализатора А (рис. 14.1) луча от угла между направлением 1 колебаний в линейно-поляризованном луче, вышедшем из поляризатора П, и направлением 2 пропускания анализатора, управляется законом Малюса
где
Закон Брюстера
Угол Брюстера iБ определяется выражением
где Линейно-поляризованный свет и в этом случае может анализироваться с помощью любого анализатора. Преломленный свет при любом угле падения на границу раздела всегда частично-поляризован и, в частности, при угле Брюстера. Преимущественное направление колебаний в преломленном луче находится в плоскости падения (преломленный свет частично-поляризован в плоскости, перпендикулярной плоскости падения).
Закон Малюса
При вращении анализатора в своей плоскости, когда направление его пропускания перпендикулярно направлению колебаний в линейно-поляризованном луче (анализатор скрещен с поляризатором), за анализатором темно. Максимальная интенсивность за анализатором имеет место, когда направление пропускания анализатора совпадает с направлением колебаний в поляризованном луче. Зависимость интенсивности вышедшего из анализатора А (см. рис. 15.1) луча от угла
I = I0соs2 φ,
где I0 - интенсивность вышедшего из анализатора луча при
Цель работы и ее выполнение Цель работы заключается в измерении концентрации Сx, раствора сахара по вращению им плоскости поляризации путем сравнения с вращением плоскости поляризации раствором сахара с известной концентрацией С. На основании формулы (15.2) можно записать
тогда
К0 - отсчет, соответствующий выравниванию яркости полуполей, когда в сахариметр помещена трубка R с дистиллированной водой; К - отсчет, соответствующий установке в прибор трубки R с раствором известной концентрации С; Кх - аналогичный отсчет, когда в прибор установлена трубка с раствором неизвестной концентрации Сx. Определение значений К повторяются пять раз, результаты заносятся в таблицу 15.1.
Таблица 15.1.
По разбросу значений K находим абсолютную ошибку Относительная погрешность определения неизвестных концентраций вычисляется по следующей формуле
Окончательно результат по каждой концентрации записывается в следующем виде
Контрольные вопросы 1. Объяснить явление поляризации света. Способы поляризации. Виды поляризованных лучей. Законы поляризации. 2. Законы вращения плоскости поляризации. 3. Для какой цели поставлен третий - добавочный - николь П1? 4. Объяснить устройство клинового компенсатора. 5. Что такое вращательная дисперсия и удельное вращение? Рекомендуемая литература 1. Савельев И. В. Курс общей физики. Изд. 2-е. Т. 3, гл. V. М., Наука, 1970. Изд. 4-е. кн. 4, гл. 6, §6.8, М., «Наука- Физматлит», 1998. 2. Яворский Б. М., Детлаф А. А. Курс физики. Т. 3, гл. 8, М., «Высшая школа», 1967 3. Калитеевский Н. И. Волновая оптика. Изд. 3-е, гл. 4, §4.5, М., «Высшая школа», 1995 4. Трофимова Т. И. Оптика и атомная физика: законы, проблемы, задачи. Гл. 3, М., «Высшая школа», 1999.
Лабораторная работа № 18 Порядок выполнения работы Первая часть работы заключается в определении длин волн линий спектра неона. Спектр неона получается при помощи неоновой лампы «тлеющего разряда». Призматический спектр в различных участках растянут различно. Одному и тому же интервалу длин волн

1. Поставить на скамью ртутную лампу. Включить. Режим включения указан на рабочем месте. 2. Необходимо снять показания, по шкале барабана монохроматора, соответствующие наиболее ярким спектральным линиям. Эти отсчеты занести в таблицу. Измерения произвести один раз, погрешность оценить в два деления шкалы барабана. 3. После выполнения градуировки ртутную лампу заменяют исследуемой лампой. 4. Измеряют положение линий спектра газа, отмечая цвет линий и занося отсчеты по барабану в таблицу. Таблица
Вторая часть работы заключается в наблюдении спектров поглощения. Если осветить щель коллиматора белым светом от нити лампы накаливания, то в окуляр виден сплошной спектр. Если между источником и щелью поместить вещество (жидкость, газ, твердое вещество), поглощающее свет определенных длин волн, то в спектре появятся темные места. Таким образом, получается спектр поглощения. Спектры поглощения находятся в соответствии со спектрами испускания (закон Кирхгофа) и по ним также можно судить о химическом составе поглощающего вещества. Определение постоянной Планка Под действием света могут происходить различные химические реакции. Например, разложение иона
Каждому поглощенному кванту света соответствует разложение одной поглотившей свет молекулы (иона). Вызвать разложение могут только те кванты, энергия которых не меньше Е1, необходимой для разложения молекулы, т.е. удовлетворяющие условию
где N0 = 6,024·1026 1/кмоль - число Авогадро; с = 3·108 м/сек- скорость распространения света в вакууме. Тогда постоянная Планка определяется из уравнения (18.1)
Порядок определения h
Щель спектрометра освещается лампой накаливания. Между щелью и лампой помещают кювету с раствором
Вычисляем относительную и абсолютную ошибки определения h и записываем результат в следующем виде
Следует соблюдать осторожность при обращении с раствором, не допуская его разбрызгивания и попадания на руки и одежду.
Контрольные вопросы 1. Различие между дифракционным и призматическим спектром. 2. Дисперсия призмы и дисперсия вещества призмы. 3. Виды спектров. Спектральный анализ. 4. Ход лучей в призматическом спектрографе.
Рекомендуемая литература 1. Савельев И.В. Курс общей физики. Изд. 4-е, кн. 4, гл. 7; кн. 5, гл. 5. М., «Наука - Физматлит», 1998г. 2. Яворский Б. М., Детлаф А. А. Курс общей физики: Т. 3, гл. VII. М., «Высшая школа», 1965г. 3. Ландсберг Г. С. Оптика. М., Наука, 1967. 4. Трофимова Т.И. «Оптика и атомная физика: законы, проблемы, задачи». Гл. 4, 8 и 9. М., «Высшая школа», 1999г. 5. Путилов К. А. Фабрикант В. А. Курс физики. Т. 3, гл. VI. М., Физматгиз, 1963.
Лабораторная работа № 20 Порядок выполнения работы
Включение лазера производится дежурным лаборантом или преподавателем. Все приборы смонтированы на оптической скамье. 1. Для выполнения первой части работы на рейтер устанавливается пластинка с ликоподием. 2. Производится отсчет положения рейтера по шкале оптической скамьи. 3. Закрепляется чистый лист бумаги на экране, фиксируется экран на скамье и снимается отсчет положения стойки по шкале скамьи. Следует стремиться к тому, чтобы расстояние между пластинкой с ликоподием и экраном было достаточно большим, чтобы дифракционные кольца наблюдать в большом масштабе. 4. Наносятся карандашом на экране окружности, представляющие середины темных колец. 5. Для выполнения второй части работы пластинка с ликоподием заменяется дифракционной решеткой 1. 6. Дифракционная решетка устанавливается так, чтобы ее щели были горизонтальными, и соответственно на экране интерференционные максимумы располагались по вертикали. Карандашом на экране наносятся положения центров светлых пятен для решетки 1. 7. Для выполнения третьей части работы на рейтер помещаются две скрещенные между собой дифракционные решетки. 8. Закрепляется чистый лист бумаги на экране и карандашом наносятся центры светлых пятен. 9. Измеряются расстояния между карандашными отметками, нанесенными в процессе выполнения работы. Диаметры окружностей промеряются в нескольких направлениях и берутся средние значения диаметров. 10. Вычисляются диаметры частиц ликоподия по формуле (20.2) на основе определения диаметра 1 и 2-го темных колец дифракционной картины. Оцениваются погрешности измерения диаметра частиц по 1 кольцу и измерения диаметра по 2-му кольцу по рабочей формуле (20.2). Предпочесть результат с меньшей относительной погрешностью 11. Вычисляется период решетки 1 по формуле (20.4) на основании средних значений результатов измерений интервалов Δу между главными максимумами интерференционной картины. Погрешность вычисляется для периода решетки тем же способом, что и погрешность размеров частиц. 12. Вычисляются периоды скрещенных решеток.
Контрольные вопросы
1. Принципы работы газовых и полупроводниковых лазеров. 2. Чем различаются индуцированное и спонтанное излучения атомов? 3. Какова роль резонатора в квантовом генераторе? 4. Что представляет собой состояние, характеризующееся отрицательной абсолютной температурой? 5. Дифракция от хаотического множества частиц и галография. 6. Дифракция от пространственной решетки.
Рекомендуемая литература 1. Савельев И. В. Курс общей физики. Изд. 2-е. Т. 3, гл.IV, XIII. М., Наука, 1970. Изд. 4-е. кн. 4, гл. 5, кн. 5, гл. 5, §§5.15,5.16. М., «Наука- Физматлит», 1998. 2. Калитеевский Н. И. Волновая оптика. Изд. 3-е, гл. 6. М., «Высшая школа», 1995 3. Трофимова Т. И. Оптика и атомная физика: законы, проблемы, задачи. Гл. 2, М., «Высшая школа», 1999.
Лабораторная работа № 21 Порядок выполнения работы 1. Включается лазер (лаборантом). 2. На пути луча лазера вблизи выходного окна помещается спектральная щель, установленная на рейтере. 3. Устанавливается экран на расстоянии Z, которое больше расстояний от центра картины на экране до используемого минимума наиболее высокого порядка. Измеряется расстояние Z от щели до экрана. 4. Щель полностью перекрывается. Вращением барабана в обратном направлении щель медленно открывается до появления отчетливой дифракционной картины. Устанавливается на барабане значение, ближайшее к найденному в сторону увеличения и кратное 10 мкм (20, 30,... мкм). На экране (листе бумаги) отмечаются карандашом положения минимумов по одну и по другую стороны дифракционной картины и записывается номер эксперимента. При переходе к очередному измерению бумага перемещается, а ширина щели увеличивается на 10 мкм. Из-за возможного люфта барабан должен вращаться каждый раз в одном направлении. 5. Измерения выполняются при 13-14 положениях ширины щели.
Обсчет результатов эксперимента выполняется следующим образом. Для определенной ширины щели измеряется расстояние между полосками заносятся в таблицу.
Таблица
Значения ширины щели b рассчитываются по формуле (21.4). Длина волны Строится график, связывающий истинные значения ширины щели с номинальными. Для этого по оси абсцисс откладываются номинальные значения ширины щели, а по оси ординат наносятся точки, представляющие измеренные истинные значения. Масштабы по осям выбирают одинаковыми. В идеальном случае график должен представлять собой прямую с наклоном 45° (теоретическая прямая). По экспериментальным точкам проводится ближайшая ко всем точкам прямая. Проводится сравнение теоретической и экспериментальной кривых и дается анализ полученных результатов, включая оценку погрешности измерений из графика.
Контрольные вопросы 1. Дифракция света от одной и двух щелей. 2. Принцип работы лазера. 3. Чем различаются индуцированное и спонтанное излучения атомов? 4. Что представляет собой состояние, характеризующееся отрицательной абсолютной температурой? 5. Какова роль резонатора в оптическом квантовом генераторе?
Рекомендуемая литература 1. Савельев И. В. Курс общей физики. Изд. 2-е. Т. 3, гл.IV, XII, XIII. М., Наука, 1970. Изд. 4-е. кн. 4, гл. 5, кн. 5, гл. 5, §§5.15,5.16. М., «Наука- Физматлит», 1998. 2. Калитеевский Н. И. Волновая оптика. Изд. 3-е, гл. 6. М., «Высшая школа», 1995. 3. Трофимова Т. И. Оптика и атомная физика: законы, проблемы, задачи. Гл. 2, гл. 9, §9.9. М., «Высшая школа», 1999.
Лабораторная работа № 70
Краткие сведения из теории
В геометрической оптике принято считать, что свет распространяется вдоль некоторых линий, называемых лучами. В основе геометрической оптики лежат четыре
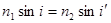 , где n1 и n2 - абсолютные показатели преломления I и II среды; i - угол падения; i' - угол преломления. , где n1 и n2 - абсолютные показатели преломления I и II среды; i - угол падения; i' - угол преломления.
Абсолютный показатель преломления вещества - Относительным показателем преломления вещества второй среды относит
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 1063; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.247.59 (0.011 с.) |


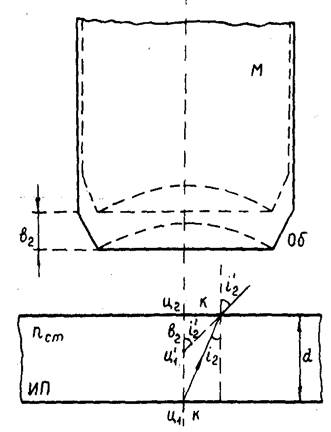 Пусть требуется определить показатель преломления nст стеклянной пластинки ИП, толщина которой d (рис. 1.1). Воспользуемся для этой цели вспомогательной пластинкой ВП, на поверхности которой нанесены штрихи ш (сетка Горяева), две царапины ц1 и ц2, на нижней и верхней поверхности пластинки ИП (рис. 1.2), и микроскопом М, объектив которого Об.
Пусть требуется определить показатель преломления nст стеклянной пластинки ИП, толщина которой d (рис. 1.1). Воспользуемся для этой цели вспомогательной пластинкой ВП, на поверхности которой нанесены штрихи ш (сетка Горяева), две царапины ц1 и ц2, на нижней и верхней поверхности пластинки ИП (рис. 1.2), и микроскопом М, объектив которого Об.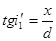 и
и 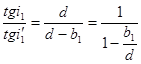 (1.1)
(1.1)
 Из рис. 1.1 видно, что
Из рис. 1.1 видно, что  ; и
; и 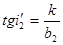 и
и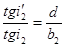 (1.2)
(1.2) - расстояние от верхней поверхности пластины ИП до видимого положения царапины ц1, нанесенной на нижнюю поверхность пластины.
- расстояние от верхней поверхности пластины ИП до видимого положения царапины ц1, нанесенной на нижнюю поверхность пластины. (1.3)
(1.3)
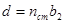 . (1.4)
. (1.4)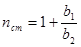 . (1.5)
. (1.5)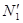 вертикального положения микроскопа, значение b1 определяется по разности отсчетов.
вертикального положения микроскопа, значение b1 определяется по разности отсчетов. , разность отсчетов равна b2.
, разность отсчетов равна b2. 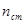 .
. .
.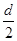 .
.
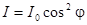 (14.1)
(14.1) - интенсивность вышедшего из анализатора луча при
- интенсивность вышедшего из анализатора луча при 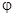 = 0.
= 0.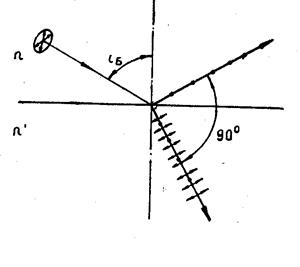 При отражении на границе раздела между двумя диэлектриками естественный свет преобразуется в частично-поляризованный с преимущественным направлением колебаний, перпендикулярным направлению падения луча. Когда угол падения луча на эту границу становится равным некоторому значению, называемому углом Брюстера или углом полной поляризации, то отраженный свет
При отражении на границе раздела между двумя диэлектриками естественный свет преобразуется в частично-поляризованный с преимущественным направлением колебаний, перпендикулярным направлению падения луча. Когда угол падения луча на эту границу становится равным некоторому значению, называемому углом Брюстера или углом полной поляризации, то отраженный свет 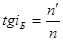 (14.2)
(14.2)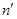 - показатель преломления среды, в которую луч входит; n - показатель преломления среды, из которой луч идет.
- показатель преломления среды, в которую луч входит; n - показатель преломления среды, из которой луч идет.

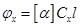
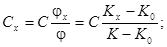
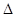 Кср. Для оценки абсолютной ошибки определения концентрации С (если она не указана) можно взять половину разряда последней значащей цифры.
Кср. Для оценки абсолютной ошибки определения концентрации С (если она не указана) можно взять половину разряда последней значащей цифры.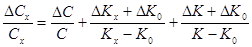
 соответствует возрастающее по мере перехода от красного к фиолетовому концу спектра линейное расстояние
соответствует возрастающее по мере перехода от красного к фиолетовому концу спектра линейное расстояние 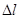 . Таким образом, для определения длин волн спектральных линий необходимо прежде всего проградуировать шкалу барабана 7 в длинах волн, т.е. найти зависимость
. Таким образом, для определения длин волн спектральных линий необходимо прежде всего проградуировать шкалу барабана 7 в длинах волн, т.е. найти зависимость 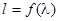 , где l - отсчет по шкале. Градуировка осуществляется с помощью известного линейчатого спектра паров ртути. Расположение и
, где l - отсчет по шкале. Градуировка осуществляется с помощью известного линейчатого спектра паров ртути. Расположение и 




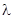 , нм
, нм
 , входящего в состав водного раствора
, входящего в состав водного раствора 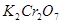 , описывается уравнением
, описывается уравнением
 . Следовательно, квант света с длиной волны
. Следовательно, квант света с длиной волны  , еще способной вызвать распад иона, удовлетворяет условию
, еще способной вызвать распад иона, удовлетворяет условию (18.1)
(18.1)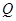 = 22,3·107 дж/кмоль (для нашего раствора) - энергия, необходимая для разложения киломоля ионов
= 22,3·107 дж/кмоль (для нашего раствора) - энергия, необходимая для разложения киломоля ионов  (18.2)
(18.2)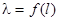 , где l - деления шкалы спектрометра, определяют
, где l - деления шкалы спектрометра, определяют 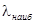 . Тогда постоянную Планка определяют по формуле (18.2). Определение
. Тогда постоянную Планка определяют по формуле (18.2). Определение  по разбросу значений
по разбросу значений 
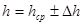
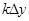 по обе стороны от центра. Данные
по обе стороны от центра. Данные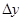
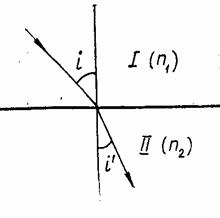
 закона: прямолинейного распространения света в однородной среде, независимости световых лучей, а также отражения и преломления света.
закона: прямолинейного распространения света в однородной среде, независимости световых лучей, а также отражения и преломления света.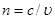 (
(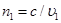 ;
;  ) показывает, во сколько раз скорость распространения света в вакууме с больше скорости распространения света в данной среде
) показывает, во сколько раз скорость распространения света в вакууме с больше скорости распространения света в данной среде  .
.


