
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Изучение кристаллов под микроскопом.Содержание книги
Поиск на нашем сайте
Основы кристаллооптики. Изучение кристаллов под микроскопом. Цель работы: изучение распространения электромагнитных волн в анизотропных средах; определение кристаллов под микроскопом в ортоскопическом и коноскопическом свете.
Введение. Для анизотропного диэлектрика становится неверной простая зависимость D = εE, которой пользуются при описании любой изотропной среды. В случае прохождения электромагнитной волны через анизотропную среду связь между D и Е задается более сложным соотношением
Эти уравнения можно переписать в более компактной форме
Девять величин являются постоянными среды и составляют тензор диэлектрической проницаемости, следовательно, вектор D равен произведению этого тензора на вектор Е. Решения уравнений Максвелла в этом случае показывают, что тензор диэлектрической проницаемости должен быть симметричным, т.е. εkl = εlk. Для любого кристалла можно найти три главных направления и связать их с координатными осями x, y, z. В этом случае тензор диэлектрической проницаемости примет диагональный вид и связь D и Е упростится
В выбранных таким образом координатах x, y, z выполняется соотношение
Это есть уравнение некого эллипсоида. Его называют эллипсоидом Френеля. Используя равенство ε = n2, уравнение можно записать в виде
Полученное уравнение есть уравнение поверхности, называемой оптической индикатрисой. В общем случае это трехосный эллипсоид.
p nz
0 ny nz y
x
Рис. 1 Оптическая индикатриса обладает следующим важным свойством. Если из её центра провести прямую 0Р вдоль распространения волнового фронта, то центральное сечение, перпендикулярное этому направлению будет эллипсом, длины полуосей которого являются показателями преломления волн, распространяющихся в направлении 0Р. Пусть в общем случае nx ≠ ny ≠ nz. В кристаллофизике их принято обозначать ng, nm, np, где ng - наибольший, а np - наименьший показатель преломления. В этом случае в индикатрисе найдутся два симметричных направления, в которых сечения будут круговыми. Эти направления будут лежать в плоскости ng, np. В этих направлениях n = const и кристалл будет вести себя как изотропная среда. Эти направления называют оптическими осями. А такие кристаллы называют двуосными. К ним относятся кристаллы триклинной, моноклинной и ромбической сингоний.
Если nm = np = no, a ng = ne, то трехосный эллипсоид превращается в эллипсоид вращения. Показатель преломления no называют обыкновенным, ne - необыкновенным. У эллипсоида вращения индикатрисы такого кристалла только одно круговое сечение, поэтому их называют одноосными. Если ne > no, то кристалл называют оптически положительным. Если ne < no, то такой кристалл называют оптически отрицательным. У оптически положительного кристалла индикатриса вытянута вдоль оптической оси, а у отрицательного - сплюснута. Для более четкого понимания прохождения света через кристаллы вводят еще ряд поверхностей, которые описывают оптические свойства кристаллов. Если в качестве главных полуосей использовать отрезки, равные Vx, Vy, Vz, то получается поверхность, описываемая в декартовой системе координат уравнением
Её называют эллипсоидом Френеля. Проанализируем несколько случаев прохождения света через одноосный
Ez ne E'z
no x y
Рис. 2
кристалл. Пусть вектор Е в падающей волне направлен вдоль оси Z, тогда для падающей волны, распространяющейся вдоль оси Х (рис. 2)
Внутри кристалла, если его оптическая ось параллельна оси Z, будет распространятся волна
Совершенно аналогичные рассуждения нас приведут к случаю, если Е || Y, т.е. после выхода из кристалла свет имеет плоскую поляризацию параллельную соответствующей оси. Пусть теперь вектор Е в падающем луче лежит в плоскости YZ и составляет угол α с осью Z (рис. 3). z
Ez ne E'z E α x no Ey y E'y
Рис. 3 Разложим Е на составляющий Ez и Ey, тогда в кристалле будут распространяться две волны со взаимно перпендикулярными колебаниями векторов Е. Они будут иметь разные скорости
В зависимости от толщины кристалла между E'z и E'y возникнет разность фаз δ и следовательно на выходе в общем случае получится эллиптически поляризованная волна. Рассмотрим более общий случай, когда естественный свет падает на границу раздела двух сред под произвольным углом и произвольной ориентацией вектора Е (рис. 4). Сориентируем оси системы координат, главные оси кристалла и световую волну так, что ne || Z, no || X, тогда рассматриваемый случай будет плоским.
ne Ey φ
x no
y φ1 φ2
Рис. 4 Заменив естественную волну двумя плоскими волнами Еz и Еy, получим
Так как ne ≠ no, то φ1 ≠ φ2, следовательно в кристалле будут распространятся две разные волны со взаимно перпендикулярными векторами Е в различных направлениях. Впервые это явление открыл Эразм Бартолини, а объяснил его с волновых позиций Гюйгенс. Оно было названо двойным лучепреломлением. Двойное лучепреломление наглядно иллюстрируют построения Гюйгенса. Пусть на границу раздела двух сред (воздух - кристалл) падает плоская волна. Если кристалл одноосный и оптически положительный, а оптическая ось параллельна границе раздела сред, то распространение света в кристалле можно изобразить поверхностями Френеля. Они описываются концом вектора скорости обыкновенной и необыкновенной волн.
Воздух
Ve
Vo
Кристалл no ne
Рис. 5
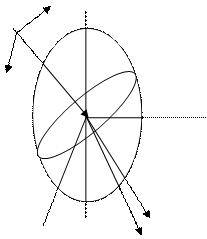
В нашем случае распространение обыкновенной волны описывается сферой, а необыкновенной эллипсоидом вращения с полуосями Vo и Ve. На рис. 5 представлены построения Гюйгенса, которые показывают, что в кристалле будут распространяться две волны "обыкновенная no" и "необыкновенная nе" по разным направлениям. Световые волны, проходя через кристаллы, проявляют интерференцию. Эти явления очень красочны и информативны. По интерференционной окраске кристаллов можно судить об осности кристаллов, ориентации оптических осей, анизотропии показателя преломления. Кристаллы наблюдают в поляризованном ортоскопическом и коноскопическом свете. Рассмотрим прохождение поляризованного света через одноосный оптически положительный кристалл. Световые волны падают на поверхность кристалла перпендикулярно его поверхности и оптической оси. Вектор напряженности электрического поля Е световой волны составляет угол α с оптической осью (рис. 6). Плоскополяризованная волна в кристалле разлагается на две волны одинаковой частоты обыкновенную Ео и
Оптическая ось
Е Ее
α Ео x
Рис. 6 необыкновенную Ее.
Пройдя через толщу кристалла, эти волны приобретут разность хода
Чтобы получить траекторию результирующего колебания, следует из этих уравнений исключить время t. Представим Х в следующем виде
Возведем последнее выражение в квадрат, а уравнение Z = Ee cosωt умножив обе части на sin φ и также возведя в квадрат, сложим с предыдущим.
и окончательно получим:
Это уравнение эллипса. Форма эллипса зависит от его полуосей и величин α и φ. Таким образом, после прохождения линейнополяризованного света через кристаллическую пластинку, получаем световую волну, конец вектора Е которой, описывает кривую с эллиптическим торцевым профилем. Такой свет называют эллиптически поляризованным. Рассмотрим несколько частных случаев. 1. Толщина кристаллической пластинки такова, что
В таком случае
Это уравнение эллипса ориентированного относительно главных осей. Величины Ео и Ее зависят от угла ориентации плоскости поляризации падающей волны относительно оптической оси кристалла "α". В частности, если α = 45о, то Ео = Ее, и тогда эллипс обращается в круг
При таком типе поляризации конец вектора Е описывает окружность. Такую поляризацию именуют циркулярной поляризацией. 2. Пусть теперь толщина кристаллической пластинки такова, что разность хода двух волн составляет
В этом случае
Это есть прямая, но повернутая на угол α относительно оптической оси кристалла симметрично плоскости поляризации падающей волны. Выходящая из такого кристалла световая волна имеет плоскую поляризацию.
3. И, наконец, пусть кристаллическая пластинка имеет толщину кратную одной длине волны.
Уравнение эллипса примет вид:
Кристаллооптический анализ. Одним из наиболее точных методов диагностики оптически анизотропных сред, кристаллов и минералов является изучение их оптических свойств при помощи особого микроскопа, оснащенного поляризационным приспособлением. Наблюдения в нем производятся в поляризованном свете как в параллельном, так и в сходящемся (коноскопическом). Поляризационный микроскоп широко используется в исследовательских институтах в практике заводских лабораторий благодаря сравнительной простоте работы с ним и высокой точности получаемых результатов. Увеличительная система микроскопа позволяет наблюдать кристаллы размерами до 1 - 2 мкм, что весьма существенно, поскольку минералы и синтетические кристаллы часто обладают мелкозернистой структурой.
Задание 1. Наблюдение двойного лучепреломления в кристалле Исландского шпата. Включить осветитель микроскопа. Установить объектив с кратностью увеличения 3,7х. Анализатор выключить. Поместить образец №1 кристалла исландского шпата на предметный столик микроскопа и добиться резкости изображений отверстия подложки. Совместив одно из изображений с центром поля зрения и вращая столик микроскопа, наблюдать поочередное погасание и просветление изображений отверстия. Распознать обыкновенный и необыкновенный лучи и ориентацию их плоскостей поляризации относительно огранки кристалла. Зарисовать результаты опытов в тетради отчетов.
Задание 2. Наблюдение положений погасания и определение Направлений колебаний света Задание 3. Определение видимой толщины шлифа кристалла кальцита Задание 4. Определение постоянной Малляра для микроскопа Дифракционным методом. Определение углового положения изохром или угла двуосности проводится по методике Малляра. Метод основан на том, что расстояние любой точки коноскопической фигуры от её центра пропорционально синусу угла, составляемого лучами, сходящимися в этой точке, с оптической осью микроскопа. Отсюда получаем известную формулу Sin V = Rd, где R - константа Малляра, d - число делений шкалы окуляр микрометра. Для определения постоянной Малляра можно измерить d у кристалла с известным углом двуосности V. Однако, есть более точный метод. Угловое положение точки в поле зрения коноскопической фигуры зададим лучами рассеянными дифракционной решеткой с периодом 1/100 мм. Направление дифракционных максимумов определится известной формулой p SinV = mλ. Используя условие Sin V = Rd, получим R = mλ/pd. Для измерения постоянной Малляра провести следующий эксперимент: 1. Установить объектив с кратностью увеличения 20х, а окуляр-микрометр - 15х, выключить анализатор. 2. Поместить на столик микроскопа дифракционную решетку с периодом 1/100 мм и сфокусировать её в поле зрения окуляра. 3. Уменьшить полевую диафрагму конденсора до минимума. 4. Ввести линзу Бертрана и отцентрировать её юстировочными винтами. 5. Наблюдать дифракционную картину в поле зрения окуляра. 6. Измерить положение желтого спектра второго, третьего и четвертого порядков по шкале окуляр микрометра с правой и с левой стороны от центра. Результаты свести в таблицу 3. 7. Рассчитать постоянную Малляра.
Таблица 3.
Задание 5. Наблюдение коноскопической фигуры одноосного кристалла Задание 6. Получение коноскопической фигуры двуосного кристалла Список рекомендуемой литературы.
1. Ландсберг Г.С. Оптика. М.: Наука. 1976. 2. Борн М., Вольф Э. Основы оптики. М.: Изд. Наука, 1970. 3. Шубников А.В. Основы оптической кристаллографии. М.: Изд. АН СССР, 1958. 4. Стойбер Р., Морзе С. Определение кристаллов под микроскопом. М.: Мир. 1974. 5. Торопов Н.А., Булак Л.И. Лабораторный практикум по минералогии. Стройиздат., Ленинград. 1969.
Основы кристаллооптики. Изучение кристаллов под микроскопом. Цель работы: изучение распространения электромагнитных волн в анизотропных средах; определение кристаллов под микроскопом в ортоскопическом и коноскопическом свете.
Введение. Для анизотропного диэлектрика становится неверной простая зависимость D = εE, которой пользуются при описании любой изотропной среды. В случае прохождения электромагнитной волны через анизотропную среду связь между D и Е задается более сложным соотношением
Эти уравнения можно переписать в более компактной форме
Девять величин являются постоянными среды и составляют тензор диэлектрической проницаемости, следовательно, вектор D равен произведению этого тензора на вектор Е. Решения уравнений Максвелла в этом случае показывают, что тензор диэлектрической проницаемости должен быть симметричным, т.е. εkl = εlk. Для любого кристалла можно найти три главных направления и связать их с координатными осями x, y, z. В этом случае тензор диэлектрической проницаемости примет диагональный вид и связь D и Е упростится
В выбранных таким образом координатах x, y, z выполняется соотношение
Это есть уравнение некого эллипсоида. Его называют эллипсоидом Френеля. Используя равенство ε = n2, уравнение можно записать в виде
Полученное уравнение есть уравнение поверхности, называемой оптической индикатрисой. В общем случае это трехосный эллипсоид.
p nz
0 ny nz y
x
Рис. 1 Оптическая индикатриса обладает следующим важным свойством. Если из её центра провести прямую 0Р вдоль распространения волнового фронта, то центральное сечение, перпендикулярное этому направлению будет эллипсом, длины полуосей которого являются показателями преломления волн, распространяющихся в направлении 0Р. Пусть в общем случае nx ≠ ny ≠ nz. В кристаллофизике их принято обозначать ng, nm, np, где ng - наибольший, а np - наименьший показатель преломления. В этом случае в индикатрисе найдутся два симметричных направления, в которых сечения будут круговыми. Эти направления будут лежать в плоскости ng, np. В этих направлениях n = const и кристалл будет вести себя как изотропная среда. Эти направления называют оптическими осями. А такие кристаллы называют двуосными. К ним относятся кристаллы триклинной, моноклинной и ромбической сингоний. Если nm = np = no, a ng = ne, то трехосный эллипсоид превращается в эллипсоид вращения. Показатель преломления no называют обыкновенным, ne - необыкновенным. У эллипсоида вращения индикатрисы такого кристалла только одно круговое сечение, поэтому их называют одноосными. Если ne > no, то кристалл называют оптически положительным. Если ne < no, то такой кристалл называют оптически отрицательным. У оптически положительного кристалла индикатриса вытянута вдоль оптической оси, а у отрицательного - сплюснута. Для более четкого понимания прохождения света через кристаллы вводят еще ряд поверхностей, которые описывают оптические свойства кристаллов. Если в качестве главных полуосей использовать отрезки, равные Vx, Vy, Vz, то получается поверхность, описываемая в декартовой системе координат уравнением
Её называют эллипсоидом Френеля. Проанализируем несколько случаев прохождения света через одноосный
Ez ne E'z
no x y
Рис. 2
кристалл. Пусть вектор Е в падающей волне направлен вдоль оси Z, тогда для падающей волны, распространяющейся вдоль оси Х (рис. 2)
Внутри кристалла, если его оптическая ось параллельна оси Z, будет распространятся волна
Совершенно аналогичные рассуждения нас приведут к случаю, если Е || Y, т.е. после выхода из кристалла свет имеет плоскую поляризацию параллельную соответствующей оси. Пусть теперь вектор Е в падающем луче лежит в плоскости YZ и составляет угол α с осью Z (рис. 3). z
Ez ne E'z E α x no Ey y E'y
Рис. 3 Разложим Е на составляющий Ez и Ey, тогда в кристалле будут распространяться две волны со взаимно перпендикулярными колебаниями векторов Е. Они будут иметь разные скорости
В зависимости от толщины кристалла между E'z и E'y возникнет разность фаз δ и следовательно на выходе в общем случае получится эллиптически поляризованная волна. Рассмотрим более общий случай, когда естественный свет падает на границу раздела двух сред под произвольным углом и произвольной ориентацией вектора Е (рис. 4). Сориентируем оси системы координат, главные оси кристалла и световую волну так, что ne || Z, no || X, тогда рассматриваемый случай будет плоским.
ne Ey φ
x no
y φ1 φ2
Рис. 4 Заменив естественную волну двумя плоскими волнами Еz и Еy, получим
Так как ne ≠ no, то φ1 ≠ φ2, следовательно в кристалле будут распространятся две разные волны со взаимно перпендикулярными векторами Е в различных направлениях. Впервые это явление открыл Эразм Бартолини, а объяснил его с волновых позиций Гюйгенс. Оно было названо двойным лучепреломлением. Двойное лучепреломление наглядно иллюстрируют построения Гюйгенса. Пусть на границу раздела двух сред (воздух - кристалл) падает плоская волна. Если кристалл одноосный и оптически положительный, а оптическая ось параллельна границе раздела сред, то распространение света в кристалле можно изобразить поверхностями Френеля. Они описываются концом вектора скорости обыкновенной и необыкновенной волн.
Воздух
Ve
Vo
Кристалл no ne
Рис. 5
В нашем случае распространение обыкновенной волны описывается сферой, а необыкновенной эллипсоидом вращения с полуосями Vo и Ve. На рис. 5 представлены построения Гюйгенса, которые показывают, что в кристалле будут распространяться две волны "обыкновенная no" и "необыкновенная nе" по разным направлениям. Световые волны, проходя через кристаллы, проявляют интерференцию. Эти явления очень красочны и информативны. По интерференционной окраске кристаллов можно судить об осности кристаллов, ориентации оптических осей, анизотропии показателя преломления. Кристаллы наблюдают в поляризованном ортоскопическом и коноскопическом свете. Рассмотрим прохождение поляризованного света через одноосный оптически положительный кристалл. Световые волны падают на поверхность кристалла перпендикулярно его поверхности и оптической оси. Вектор напряженности электрического поля Е световой волны составляет угол α с оптической осью (рис. 6). Плоскополяризованная волна в кристалле разлагается на две волны одинаковой частоты обыкновенную Ео и
Оптическая ось
Е Ее
α Ео x
Рис. 6 необыкновенную Ее.
Пройдя через толщу кристалла, эти волны приобретут разность хода
Чтобы получить траекторию результирующего колебания, следует из этих уравнений исключить время t. Представим Х в следующем виде
Возведем последнее выражение в квадрат, а уравнение Z = Ee cosωt умножив обе части на sin φ и также возведя в квадрат, сложим с предыдущим.
и окончательно получим:
Это уравнение эллипса. Форма эллипса зависит от его полуосей и величин α и φ. Таким образом, после прохождения линейнополяризованного света через кристаллическую пластинку, получаем световую волну, конец вектора Е которой, описывает кривую с эллиптическим торцевым профилем. Такой свет называют эллиптически поляризованным. Рассмотрим несколько частных случаев. 1. Толщина кристаллической пластинки такова, что
В таком случае
Это уравнение эллипса ориентированного относительно главных осей. Величины Ео и Ее зависят от угла ориентации плоскости поляризации падающей волны относительно оптической оси кристалла "α". В частности, если α = 45о, то Ео = Ее, и тогда эллипс обращается в круг
При таком типе поляризации конец вектора Е описывает окружность. Такую поляризацию именуют циркулярной поляризацией. 2. Пусть теперь толщина кристаллической пластинки такова, что разность хода двух волн составляет
В этом случае
Это есть прямая, но повернутая на угол α относительно оптической оси кристалла симметрично плоскости поляризации падающей волны. Выходящая из такого кристалла световая волна имеет плоскую поляризацию.
3. И, наконец, пусть кристаллическая пластинка имеет толщину кратную одной длине волны.
Уравнение эллипса примет вид:
|
|||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 626; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.18.97 (0.013 с.) |







 z
z
 z
z .
.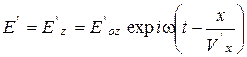 , где V'x = c/ne.
, где V'x = c/ne.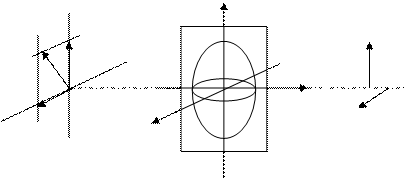

 Ez z
Ez z ,
, 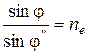 .
.
 z
z

 или разность фаз
или разность фаз  . Сложение двух взаимно перпендикулярных колебаний с разными амплитудами и разными фазами дадут нам новую волну с той же частотой. Координата вектора Е по осям х и z будет изменяться по закону
. Сложение двух взаимно перпендикулярных колебаний с разными амплитудами и разными фазами дадут нам новую волну с той же частотой. Координата вектора Е по осям х и z будет изменяться по закону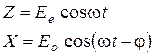 или
или 
 или
или 


 .
.
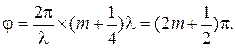 Уравнение эллипса примет вид:
Уравнение эллипса примет вид: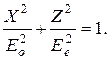
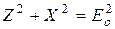 .
.
 , а уравнение эллипса преобразуется к виду:
, а уравнение эллипса преобразуется к виду: .
.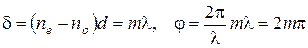 .
. . Это есть прямая, которая имеет ориентацию вектора Е такой же, как и в падающей плоскополяризованной волне. Выходящий из кристалла свет плоскополяризован.
. Это есть прямая, которая имеет ориентацию вектора Е такой же, как и в падающей плоскополяризованной волне. Выходящий из кристалла свет плоскополяризован.


