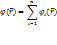Напряжённость электрического поля точечного заряда

Для точечного заряда в электростатике верен закон Кулона

или

Электростатическое поле — поле, созданное неподвижными в пространстве и неизменными во времени электрическими зарядами (при отсутствии электрических токов).

Электрическое поле представляет собой особый вид материи, связанный с электрическими зарядами и передающий действия зарядов друг на друга.

Если в пространстве имеется система заряженных тел, то в каждой точке этого пространства существует силовое электрическое поле. Оно определяется через силу, действующую на пробный точечный заряд, помещённый в это поле. Пробный заряд должен быть ничтожно малым, чтобы не повлиять на характеристику электростатического поля.

Электрическое поле называют однородным, если вектор его напряженности одинаков во всех точках поля.

Основные характеристики электростатического поля:

· напряженность

· потенциал

Принцип суперпозиций -если поле образовано не одним зарядом, а несколькими, то силы, действующие на пробный заряд, складываются по правилу сложения векторов. Поэтому и напряженность системы зарядов в данной точке, поля равна векторной сумме напряженностей полей от каждого заряда в отдельности.
4. Поток векторного поля E. Теорема Гаусса для поля вектора E в вакууме в интегральной форме, ее содержательный смысл.

Поток векторного поля через поверхность — поверхностный интеграл второго рода по поверхности S. По определению

Теорема Гаусса для поля вектора Е в вакууме:

Поток вектора Е электростатического поля в вакууме через любую замкнутую поверхность (S) равен алгебраической сумме зарядов q(вн), охватываемых этой поверхностью.

Содержательный смысл: заряд является источником электрического поля.

5.Дивергенция поля вектора Е. Теорема Гаусса для поля вектора Е в вакууме в дифференциальной форме и ее содержательный смысл.
Дивергенция — это линейный дифференциальный оператор на векторном поле, характеризующий поток данного поля через поверхность достаточно малой (в условиях конкретной задачи) окрестности каждой внутренней точки области определения поля.

Теорема Гаусса для поля вектора Е в вакууме в дифференциальной форме устанавливает связь между объемной плотностью заряда в некоторой точке поля.

Потенциальность электростатического поля. Циркуляция поля вектора Е. Теорема о циркуляции вектора Е электростатического поля в инт. и диф. формах, их содержательный смысл.

Так как для напряженности электростатического поля справедлив принцип суперпозиции, то потенциальным является любое электростатическое поле.

Теорема о циркуляции вектора Е электростатического поля: Циркуляция Е по замкнутому контуру L всегда равно нулю.

В диф. форме:

Электростатическое поле является потенциальным.

 

Потенциальная энергия точечного заряда в электростатическом поле. Потенциал электростатического поля. Эквипотенциальные поверхности. Потенциал поля точечного неподвижного заряда. Принцип суперпозиции для потенциала.

Потенциальная энергия заряда в однородном электростатическом поле равна:

Потенциал – скалярная величина, является энергетической характеристикойполя в данной точке и равный отношению потенциальной энергии, которой обладает пробный заряд, к этому заряду.

Эквипотенциальная поверхность – это поверхность, на которой потенциал данного поля принимает одно и то же значение.

Потенциал поля точечного неподвижного заряда:

Принцип суперпозиций для потенциалов - Потенциал поля, созданного ГРУ ппой зарядов в произвольной точке равен сумме потенциалов полей, созданных каждым зарядом.

Градиент скалярного поля. Связь между вектором напряженности электростатического поля и потенциалом.

 

Градиент — вектор, своим направлением указывающий направление наибольшего возрастания некоторой величины φ, значение которой меняется от одной точки пространства к другой.

Вектор напряженности электростат. поля равен градиенту потенциала в данной точке поля с обратным знаком.