
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сила Ампера. Взаимодействие параллельных токов.Содержание книги
Поиск на нашем сайте Сила ампера – сила, действующая на проводник с током в магнитном поле.
Модуль силы Ампера:
Два параллельных бесконечно длинных проводника с токами Модуль силы магнитного взаимодействия, приходящийся на единицу длины:
Контур с током в магнитном поле. Момент сил, действующих на контур с током, и потенциальная энергия контура с током в однородном магнитном поле. Работа сил магнитного поля при перемещении контура с током. Магнитный момент
S – площадь поверхности, ограниченной контуром; в СИ [ Результирующая сила Ампера, действующая на контур с током в однородном магнитном поле равна 0. Поэтому суммарный момент амперовых сил не зависит от выбора точки О, относительно которой он вычисляется:
Момент сил, действующий на замкнутый контур с током I в магнитном поле индукции
При При Потенциальная энергия
Работа сил Ампера:
При этом направление положительной нормали 29. Магнитное поле в веществе. Намагничение диа- и парамагнетиков. Вектор намагниченности Любое вещество – магнетик (т.е. способно намагничиваться под действием внешнего магнитного поля) Ток проводимости (I, Молекулярные токи ( Диамагнетики – вещества, магнитные моменты атомов которых в отсутствие внешнего магнитного поля равны нулю, т.е. магнитные моменты всех элементарных частиц атома (молекулы) скомпенсированы. Парамагнетики – вещества, атомы которых в отсутствие внешнего магнитного поля имеют отличный от нуля магнитный момент, но их направление ориентировано хаотично, поэтому При внесении во внешнее магнитное поле При внесении во внешнее магнитное поле парамагнетика магнитный момент его атомов (молекул) приобретают ориентированную по направлению внешнего поля Намагничение вещества обусловлено приемущественной ориентацией или индуцирование отдельных молекул в одном направлении. Намагничение вещества приводит к возникновению токов намагничения
где Согласно принципу суперпозиции:
где
Вектор намагниченности
В СИ [J] = А/м. Теорема о циркуляции вектора в любой точке магнитостатического поля ротор вектора
Теорема о циркуляции поля вектора циркуляция вектора намагниченности магнитостатического поля по любому замкнутому конуру (L) равна алгебраической сумме токов намагничивания J’, охватываемых этим контуром:
30. Вектор напряженности Величина: - вектор напряженности магнитного поля. Теорема о циркуляции вектора
Теорема о циркуляции поля вектора
Циркуляция вектора Для изотропных диамагнитных и парамагнитных сред
где
где 31.Условия на границе раздела двух магнетиков для векторов Вблизи поверхности раздела двух изотропных магнетиков (при отсутствии токов проводимости) поля вектора
на границе раздела 2-ух магнетиков: 1)нормальная составляющая вектора 2)тангенциальная составляющая вектора Закон преломления силовых линий вектора
|
||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 501; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.008 с.) |

 обусловлена действием на каждый направленно движущийся носитель тока магнитной составляющей
обусловлена действием на каждый направленно движущийся носитель тока магнитной составляющей  :
: - Сила Ампера, действующая на элемент тока (
- Сила Ампера, действующая на элемент тока (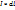 ) в магнитном поле индукции
) в магнитном поле индукции  .
.
 , находящихся в вакууме на расстоянии b друг от друга, взаимодействуют с силой притяжения в случае с одинаково направленных токов или с силой отталкивания в случае противоположно направленных токов.
, находящихся в вакууме на расстоянии b друг от друга, взаимодействуют с силой притяжения в случае с одинаково направленных токов или с силой отталкивания в случае противоположно направленных токов.
 линейного тока I, идущего по замкнутому плоскому контуру (все точки которого лежат в одной плоскости):
линейного тока I, идущего по замкнутому плоскому контуру (все точки которого лежат в одной плоскости):
 ] = А*
] = А* 


 M=0 (т.е. контур с током находится в положении равновесия).
M=0 (т.е. контур с током находится в положении равновесия). на контур действует максимальный момент сил
на контур действует максимальный момент сил  .
. замкнутого контура с током в магнитном поле:
замкнутого контура с током в магнитном поле:

 образует правовинтовую систему. Данная формула справедлива в случае произвольного перемещения контура любой формы в магнитном поле.
образует правовинтовую систему. Данная формула справедлива в случае произвольного перемещения контура любой формы в магнитном поле. . Теорема о циркуляции поля вектора
. Теорема о циркуляции поля вектора  ) – ток, обусловленный направленным движением в веществе носителей тока.
) – ток, обусловленный направленным движением в веществе носителей тока. ) – токи, связанные с орбитальным движением и спином элементарных частиц в атомах вещества. Каждый молекулярный ток обладает магнитным моментом.
) – токи, связанные с орбитальным движением и спином элементарных частиц в атомах вещества. Каждый молекулярный ток обладает магнитным моментом. .
. диамагнетика в каждом его атоме индуцируется дополнительный момент
диамагнетика в каждом его атоме индуцируется дополнительный момент 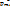 , направленный против внешнего магнитного поля
, направленный против внешнего магнитного поля 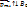 .
. .
. (усредненные по макроскопической области молекулярные токи):
(усредненные по макроскопической области молекулярные токи):
 - вектор плотности тока намагничивания, идущего через ориентированную поверхность S.
- вектор плотности тока намагничивания, идущего через ориентированную поверхность S.
 - индукция магнитного поля токов намагничивания.
- индукция магнитного поля токов намагничивания. – количественная характеристика намагниченного состояния вещества, равная отношению суммарного магнитного момента физически малого объема магнетика у этому объему
– количественная характеристика намагниченного состояния вещества, равная отношению суммарного магнитного момента физически малого объема магнетика у этому объему  :
:


 магнитного поля. Теорема о циркуляции поля вектора
магнитного поля. Теорема о циркуляции поля вектора 
 магнитостатического поля в дифференциальной форме:
магнитостатического поля в дифференциальной форме:
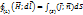
 :
:
 - магнитная восприимчивость, характерная для каждого магнетика:
- магнитная восприимчивость, характерная для каждого магнетика:
 - магнитная проницаемость вещества.
- магнитная проницаемость вещества. . Закон преломления силовых линий.
. Закон преломления силовых линий. удовлетворяют условиям:
удовлетворяют условиям:







