
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уравнение непрерывности (закон сохранения заряда в диф. форме), его содержательный смысл. Условие стационарности электрического тока.Содержание книги
Поиск на нашем сайте Уравнение непрерывности – аналитическое выражение закона сохранения электрического заряда.:
Содержательный смысл: в точках, которые являются ист. поля вектора Если в каждой точке области эл. тока вектор пл. Тогда
Из последних 2-х ур. следует, что силовые линии стационарного тока не имеют точечных источников и являются замкнутыми. Сторонние силы. ЭДС. Напряжение. Закон Ома в интегральной и дифференциальной форме. Т.к. работа сил э-статического поля вдоль любой замкнутой траектории равна нулю, то для длит. поддержания тока в замкнутом проводнике действия на носители тока только э-статического поля недостаточно. Поэтому на каком-либо участке должны действовать сторонние силы. Сторонние силы – силы неэлектростатического происхождения, действующие на заряд. Всякое устройство, в кот. действуют стор. силы, называется источником эл. тока. ЭДС – скалярная физ. величина, равная отношению работы Астор при переносе заряда q на участке проводника, к этому заряду.
Напряжение U на уч. проводника – скалярная физ. величина, равная отношению работы всех сил при переносе заряда, к этому заряду.
Значит Участок проводника, на кот. не действ. сторонние силы, называется однородным (для него Закон Ома в интегральной форме: Сила тока I, идущего на участке проводника, прямо пропорциональна напряжению U на участке:
В СИ [G] = Cм (Сиеменс) Величина, обратная проводимости, наз. сопротивлением: В СИ [R] = Ом Сопротивление R участка изотропного пров. длиной l и площадью поперечного сечения S
В дифференциальной форме устанавливается зависимость между вектором пл. тока напряженности
Закон Джоуля-Ленца в интегральной и в дифференциальной форме. Удельная тепловая Мощность электрического тока. Закон Джоуля-Ленца в интегр. форме: при прохождении эл. тока через пров., в котором отсутствует хим. превращения, в нем выдел. количество теплоты, равное: За конечный промежуток времени в проводнике выдел. количество теплоты, равное:
Удельная тепловая мощность тока в т. проводника при прохождении эл. тока:
Закон Джоуля-Ленца в дифференциальной форме: удельная тепловая мощность в точке срадиус-вектором
Данное ур. представляет собой наиболее общую форму закона Джоуля-Ленца, применимую для люб. проводников вне зависимости от их формы и природы сил, возбуждающих эл. ток Магнитостатическое поле в вакууме. Опыт Эрстеда. Электрическая и магнитная составляющая силы взаимодействия 2-х движущихся зарядов. Вектор магнитной индукции Равномерно движущегося заряда. Силовые линии магнитного поля. Над магнитной стрелкой параллельно её располагают мет. проводник, при пропуск. через него эл. тока стрелка поворачивалась перпенд. проводнику. При изм. направления тока или при переносе провода под стрелку она разворачивалась на В опыте Эрстеда впервые было замечено действие проводника с током на магнитную стрелку, что указывало на связь между электрич. и магнитными явлениями. Движущийся эл.заряд создает не только электрическое, но и магнитное поле.
Силу 2-х составляющих: электрической и магнитной
зарядом В СИ [B] = Тл Линия, касательная к которой в каждой точке содержит вектор магнитного поля Магнитостатика – раздел электромагнетизма, изучающий магнитные поля, созд. постоянными токами.
|
||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 587; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |


 эл. заряд со временем убывает.
эл. заряд со временем убывает.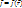
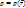 и
и 
 – условие стационарности эл. тока
– условие стационарности эл. тока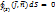
 ; В СИ [
; В СИ [  ]=В;
]=В;  ; В СИ [
; В СИ [  ]=В
]=В ;
;  ;
;
 )
)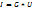 , где G – проводимость участка.
, где G – проводимость участка.
 , где
, где  – удельное сопротивление проводника
– удельное сопротивление проводника
 в этой же точке с радиус-вектором
в этой же точке с радиус-вектором 
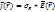 ;
; – удельная электропроводимость среды:
– удельная электропроводимость среды:  ; В СИ [
; В СИ [ 
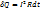

 – величина, характеризующая мощность теплоты, выделяемой
– величина, характеризующая мощность теплоты, выделяемой ;
;  –количество теплоты, выдел. за время dt в малом объеме dV
–количество теплоты, выдел. за время dt в малом объеме dV
 . Магнитное поле
. Магнитное поле .
. – магнитная постоянная, равная 4*10-7 Гн
– магнитная постоянная, равная 4*10-7 Гн , с которой движущийся заряд
, с которой движущийся заряд  действует на движ. заряд q можно предст. в виде
действует на движ. заряд q можно предст. в виде

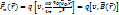

 – вектор индукции магнитного поля, созд. движ. со скор.
– вектор индукции магнитного поля, созд. движ. со скор.  точечным
точечным , называется силовой линией
, называется силовой линией


