
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод нахождения общего порядка реакцииСодержание книги
Поиск на нашем сайте Для нахождения общего порядка реакции необходимо взять реагенты в стехиометрическом соотношении. Если стехиометрическое уравнение реакции: аА + вВ → продукты то при СА : СВ = а: в, Тогда кинетическое уравнение примет вид:
Далее логарифмирование приведет к линейной зависимости
Метод по доле непревращенного вещества к моменту времени t Если
получаем:
Интегрирование в пределах (а = 1; а) и (t = 0; t) приводит к уравнению:
Уравнение сложно для расчета «n», поэтому его применяют в двух частных случаях: а) проводят ряд опытов, в которых взяты разные начальные концентрации, но во всех опытах реакция доведена до одинаковой доли а. В таких условиях левая часть уравнения (3.9) постоянна, обозначим ее В:
Полученное уравнение прямой в координатах (lnt; lnC0) позволяет графически найти «n», поскольку Если проведено два опыта с одинаковым значением а, то, записав уравнение 3.10 для обоих опытов и вычитая одно из другого, получаем уравнение для n:
-
б) Можно определить порядок, располагая одной полной кинетической кривой. Выбирают на кривой два значения а, связанные между собой соотношением: При этом скобка в левой части уравнения (3.9) для а2 будет иметь вид:
Записав уравнение (3.9) для второго опыта и для первого и поделив уравнения одно на другое получаем, сократив общие множители:
После логарифмирования получаем:
Сложные реакции Сложная реакция состоит из нескольких элементарных стадий, связанных друг с другом определенным образом через исходные вещества и промежуточные продукты. В отношении сложных реакций в кинетике возникают две задачи. Прямая задача. Известны механизм и константы скорости каждой элементарной стадии. Необходимо для конкретных условий (Т, Сi) описать кинетическое поведение каждого молекулярного продукта. Это достигается составлением и решением системы дифференциальных уравнений. Зная (вычислив) кинетические кривые для всех веществ, можно рассчитать скорость отдельных стадий для разных моментов времени протекания реакции. Обратная задача. Экспериментально получают набор кинетических кривых и на основании полученных результатов проверяют предполагаемую схему реакции, определяют порядок и константу скорости каждой из стадий. В сложных реакциях действует принцип независимости реакций, согласно которому: если в системе одновременно протекает несколько реакций, каждая из них независима от других реакций и будет протекать со скоростью, определяющейся своим дифференциальным уравнением и своей константой скорости. Из этого принципа следует условие материального баланса: если в результате протекания химических реакций исчезает или появляется какой-либо компонент, то скорость изменения концентрации этого вещества будет равна алгебраической сумме скоростей его образования и расходования во всех стадиях, то есть
где n – число элементарных стадий, в которых участвует i компонентов; νi – стехиометрический коэффициент i -го компонента в данной стадии, для исходных веществ νi < 0, для продуктов νi > 0; υ – скорость реакции в единичном объеме в данной стадии, определяется кинетическим уравнением υ = k СаАСвВ (А и В – исходные вещества в данной системе). Рассмотрим пример. k1 A + 1/2B k2
Эта сложная реакция может быть расписана в две строчки k1 A + 1/2B k2 C + 2D
Обе записи тождественны. Запишем условие материального баланса для компонента D. Он участвует в трех стадиях (n = 3) с константами скоростей k1, k2 и k3
Таким образом, произведений νD . υ будет три. νD в реакции 1, где D является продуктом, равна +2; а в реакциях 2 и 3, где D является исходным веществом, νD = -2.
Аналогично для вещества В:
Параллельные реакции При параллельных реакциях одно и то же вещество (или вещества) участвует в нескольких реакциях, давая различные продукты. Например, разложение бертолетовой соли возможно по двум реакциям
Рассмотрим простейший случай – две параллельные реакции первого порядка. Получим уравнения для расчета констант реакции k1 и k2:
В начальный момент (t = 0) в системе присутствует только вещество А с концентрацией a, к моменту времени t концентрация a уменьшилась на x, появилось x1 вещества В и х2 вещества D. Составим дифференциальное уравнение для вещества А. Решая его, найдем k1 и k2.
Составим дифференциальные уравнения для веществ В и D.
Разделив уравнение (3.13) на (3.14), получим
Решая систему уравнений (3.12) и (3.15), находим k1 и k2. Поскольку взята реакция мономолекулярная, следовательно, количество израсходованного вещества А равно сумме получившихся веществ В и D, то есть х = х 1 + х 2
Обратимые реакции Обратимыми (двусторонними) в кинетике называют реакции, которые протекают одновременно, как в прямом, так и в обратном направлении. В этом смысле почти все химические реакции являются двусторонними. В ходе их протекания исходные вещества образуют продукты, которые, вступая во взаимодействие между собой, образуют снова молекулы исходных веществ. Пока скорости этих процессов неодинаковы, происходят заметные изменения количества реагентов. Если скорости прямого и обратного процессов становятся равными, то наступает динамическое равновесие. В этом случае концентрации реагентов перестают изменяться и подчиняются термодинамическому закону действующих масс. Если же скорость обратной неизмеримо меньше скорости прямой реакции, то такая реакция считается кинетически необратимой. Это может произойти, если продукты быстро удаляются из зоны реакции и не успевают вступать во взаимодействие. Например, при выделении газа или выпадении осадка. Заметим, что обратимые (двусторонние) реакции в кинетике не соответствуют термодинамически обратимому процессу. В первом случае речь идет о направлении процесса, во втором – о способе его проведения. Рассмотрим наиболее простой тип обратимых реакций с мономолекулярными стадиями. Задача состоит в определении констант прямой и обратной реакций. k1 А k2 t = 0 a 0 t a - x x t = ∞ a - xравн. xравн.
Составим дифференциальное кинетическое уравнение для А.
В момент равновесия
В любой момент времени t, заменив в уравнении (3.16) (k1+k2) из уравнения (3.17), и СА = (a – x)
Таким образом, зная концентрации реагента в начальный момент времени и в момент времени t, а также в момент равновесия, можно определить k1 и k2 по уравнениям (3.18) и (3.19). х равн. может быть найдено по закону действующих масс, если известна константа равновесия. При равновесии
то есть, отношение констант скоростей прямой и обратной реакций равно константе равновесия обратимой реакции. k 1 и k 2 можно найти, решая систему уравнений (3.19) и (3.20). Можно получить уравнение для количества прореагировавшего вещества А в любой момент времени t. Из уравнения (3.19)
Последовательные реакции Последовательные реакции состоят из нескольких стадий, следующих друг за другом. Примером является реакция гидролиза трисахаридов в кислой среде: С18Н32О16 + Н2О → С6Н12О6 + С12Н22О11 Промежуточными продуктами могут быть обычные молекулы, свободные атомы или радикалы, обладающие повышенной химической активностью. Математическое решение уравнений для последовательных реакций является довольно сложным и целесообразно лишь для простейших случаев. Рассмотрим реакцию, состоящую из двух простых мономолекулярных стадий:
t = 0 C0A 0 0 t C0A – x x – y y, где (х – у) и у – концентрации веществ В (CB) и D (CD) в момент времени t, соответственно. Реакция превращения вещества А идет по первому порядку и текущая концентрация вещества А рассчитывается по уравнению (3.3) СА = С0А e-k1t. Приведем уравнение текущей концентрации вещества В (без вывода) СВ = Ввиду того, что обе стадии мономолекулярны и расходование некоторого количества молекул А приводит к образованию точно такого же количества молекул В, а затем из В образуется D, выполняется равенство С0А = СА + СВ + СD, откуда СD = С0А - С0А . e-k1t -
Полученные зависимости могут быть представлены графически в виде кинетических кривых (рисунок 3.9).
Рисунок 3.9 – Зависимость концентраций участников последовательной реакции от времени
Для вещества А кривая представляет собой экспоненту. Кривая вещества В проходит через максимум. Время tmax можно найти, если взять первую производную
Из уравнения (3.23) видно, что время, необходимое для достижения максимального значения СВ зависит от соотношения констант. Чем больше Обратимся к конечному продукту D. Скорость его образования зависит от концентрации вещества В: В начальный период, когда концентрация вещества В невелика, образование D идет с очень малой скоростью и аналитически не обнаруживается. Такой начальный период реакции называют периодом индукции, tинд. Далее кривая имеет S-образный вид, максимальная скорость роста приходится на максимальную концентрацию В, то есть при tmax (B), здесь линия имеет перегиб и дальнейший рост концентрации D замедляется. Любой процесс, состоящий из ряда последовательных стадий, определяется самой медленной стадией, тормозящей весь процесс. Эта стадия называется лимитирующей. Выясним условия, когда одна стадия становится лимитирующей, определяющей выход продукта D. Запишем скорость образования D.
Рассмотрим два крайних случая: 1. Если k1 «k2, то в уравнении (3.24) величиной k1 в знаменателе можно пренебречь. Поскольку e-k2t «e-k1t, то в скобках останется e-k1t. Таким образом,
то есть скорость образования продукта определяется первой стадией, которая и будет в этих условиях лимитирующей. 2. Если k1» k2, пренебрегаем в алгебраических суммах величинами k2 (в знаменателе) и e-k1t (в скобках).
в данном случае лимитирующей стадией будет вторая.
Сопряженные реакции Химическая индукция – такое явление, когда одна химическая реакция вызывает (индуцирует) протекание в системе другой, неосуществимой в отсутствие первой. Две реакции, из которых одна индуцирует протекание другой, называются сопряженными. Схема сопряженной реакции в простейшем случае: 1. А + С 2. А + J → В (реакция идет самостоятельно);
Часто в обеих реакциях принимает участие одно и то же вещество, которое самопроизвольно реагирует во второй реакции. Это вещество называется актором (в нашем случае вещество А). Компонент, который реагируя с актором, индуцирует превращение другого вещества в другой реакции, называется индуктором (вещество J). Компонент, который вступает в реакцию с актором только в присутствии индуктора, называется акцептором (вещество С). Например, реакция 2СО + О2→2СО2 Идет только при достаточно высоких температурах. Но если в системе протекает реакция окисления водорода 2Н2 + О2 → 2Н2О, то в этой системе окисляется и СО при невысоких температурах. В этих сопряженных реакциях кислород О2 является актором, Н2 – индуктором, а СО – акцептором. Явление химической индукции было подробно исследовано Н.А.Шиловым. Им было дано объяснение этому явлению, согласно которому химическая индукция обусловлена тем, что сопряженные реакции протекают через общие активные промежуточные вещества. Такими активными промежуточными продуктами могут быть свободные радикалы, промежуточные окисленные формы ионов, лабильные комплексы и так далее. Тогда схема простейших сопряженных реакций будет содержать активное промежуточное вещество R и примет вид: A + J R + J R + C Таким образом, в сопряженных реакциях образующиеся активные промежуточные вещества взаимодействуют как с индуктором, так и с акцептором, вызывая расходование последнего. В приведенном выше примере индукция обусловлена образованием радикала гидроксила НО ∙ в цепной реакции окисления водорода, который окисляет и СО НО ∙ + СО → СО2 + Н ∙ Количественной мерой химической индукции служит фактор индукции Ф, который представляет собой отношение скорости расходования акцептора,
Однако, полученное уравнение не может быть рассчитано практически, поскольку в формулу входит СR – концентрация неустойчивого промежуточного продукта, которая не может быть определена аналитически. Для такого типа реакций предложен приближенный метод стационарных концентраций, позволяющий избежать использования концентрации СR. Рассмотрим этот метод подробнее.
|
||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 400; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.009 с.) |

 .
.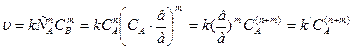 .
.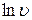 от
от  и определению (n + m) как тангенс угла наклона (аналогично нахождению в методах 3 и 4).
и определению (n + m) как тангенс угла наклона (аналогично нахождению в методах 3 и 4). - доля исходного вещества, не вступившего в химическую реакцию к моменту времени t, то
- доля исходного вещества, не вступившего в химическую реакцию к моменту времени t, то  . Подставляя выражение для С в уравнение
. Подставляя выражение для С в уравнение


 . (3.9)
. (3.9)
 .
.

 и отвечающие этим значениям t2 и t1.
и отвечающие этим значениям t2 и t1. .
. ,
, ,
, .
. .
. (3.11)
(3.11) C + 2D
C + 2D  E.
E.
 2k1CAC
2k1CAC  – 2k2CC C
– 2k2CC C  – 2k3CC C
– 2k3CC C  = - 1/2 k1CAC
= - 1/2 k1CAC 


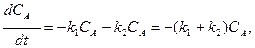



 (3.13)
(3.13) (3.14)
(3.14)
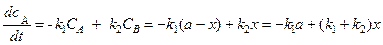 . ( 3.16)
. ( 3.16)

 . ( 3.17)
. ( 3.17) ,
,




 откуда получаем
откуда получаем
 (3.21)
(3.21) 3С6Н12О6
3С6Н12О6
 (e-k1t - e-k2t). (3.22)
(e-k1t - e-k2t). (3.22)
 и приравнять ее к нулю (условие экстремума).
и приравнять ее к нулю (условие экстремума). . (3.23)
. (3.23) .
. (e-k1t - e-k2t). (3.24)
(e-k1t - e-k2t). (3.24) e-k1t =
e-k1t =  ,
, e-k2t,
e-k2t,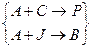 реакции идут совместно в одной системе
реакции идут совместно в одной системе R
R B
B P
P , к скорости расходованияиндуктора,
, к скорости расходованияиндуктора,  , то есть
, то есть .
.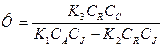 . (3.25)
. (3.25)


