
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Гоу впо «алтайский государственный техническийСодержание книги
Поиск на нашем сайте
Российской Федерации ГОУ ВПО «Алтайский государственный технический университет им. И. И. Ползунова» М. Ф. Стенникова, Н. П. Мусько, О. С. Беушева, Н. Г. Комарова Руководство По физической химии Учебное пособие Часть II Барнаул 2010 М. Ф. Стенникова, Н. П. Мусько, О. С. Беушева, Н. Г. Комарова Руководство По физической химии Учебное пособие в 2-х частях Часть II Барнаул 2010 УДК 541.1
Стенникова М. Ф. Руководство по физической химии: учебное пособие / М. Ф. Стенникова, Н. П. Мусько, О. С. Беушева, Н. Г. Комарова. – Барнаул: Изд-во АлтГТУ, 2010.- 107 с.
Рассмотрено и одобрено кафедрой ТППЭ Протокол № от 24.03.10
Рекомендовано Алтайским государственным техническим университетом им. И. И. Ползунова в качестве учебного пособия для студентов АлтГТУ, обучающихся по специальностям: 280201 ООС; 240801 МАХП; 260201 ТПЗ; 260501 ТОП; 260204 ТБПВ; 260303 ТМП; 260202 ТХ.
Содержание 1 РАСТВОРЫ... 5 1.1 Основные понятия и определения. 5 1.2 Способы выражения состава раствора. 5 1.3 Закон Рауля. Идеальные растворы.. 6 1.4 Следствия из закона Рауля. 8 1.4.1 Повышение температуры кипения идеального раствора. 8 1.4.2 Понижение температуры замерзания раствора. 9 1.5 Осмотическое давление. 10 1.6 Реальные растворы.. 12 1.6.1 Отклонения от закона Рауля. 12 1.7 Растворимость. 15 1.7.1 Растворимость твердых веществ в жидкости. 15 1.7.2 Растворимость газов в жидкости. 16 1.7.3 Взаимная растворимость жидкостей. 18 1.8 Равновесие жидкий раствор – насыщенный пар в различных жидких смесях. 19 1.8.1 Неограниченно смешивающиеся жидкости. 19 2 ЭЛЕКТРОХИМИЯ.. 36 2.1 Электрическая проводимость растворов электролитов. 36 2.1.1 Сильные и слабые электролиты.. 36 2.1.2 Удельная электрическая проводимость. 37 2.1.3 Молярная и эквивалентная электрические проводимости. 39 2.2 Кондуктометрия. 42 2.2.1 Определение растворимости труднорастворимой соли. 42 2.2.2 Определение предельной эквивалентной электрической проводимости растворов сильных электролитов. 43 2.2.3 Кондуктометрическое титрование. 43 2.3 Электродные процессы.. 44 2.3.1 Основные понятия и определения. 44 2.3.2 Классификация электродов. 47 2.3.3 Типы гальванических элементов. 50 2.3.4 Диффузионный потенциал. 51 2.3.5 Потенциометрическое титрование. 52 2.4.3.3 Законы Фарадея. 62 2.5 Примеры решения задач. 63 2.6 Вопросы для самоконтроля. 71 3 КИНЕТИКА.. 72 3.1 Скорость химической реакции. 72 3.2 Кинетическая классификация химических реакций. 74 3.2.1 Молекулярность реакции. 75 3.2.2 Порядок реакции. 76 3.3 Влияние температуры на скорость реакции. Энергия активации. 80 3.4 Методы определения порядка реакции. 84 3.4.1 Параллельные реакции. 90 3.4.2 Обратимые реакции. 91 3.4.3 Последовательные реакции. 92 3.4.4 Сопряженные реакции. 95 3.4.5 Метод стационарных концентраций. 96 3.5 Примеры решения задач. 99 3.6 Вопросы для самоконтроля. 106 Литература. 107
РАСТВОРЫ
1.1 Основные понятия и определения
Раствор – это многокомпонентная, гомогенная, термодинамически равновесная система, образованная за счет всех возможных сил взаимодействия между всеми составляющими ее частицами. Раствор образуется из компонентов самопроизвольно. Поэтому, его образование при постоянных температуре и давлении, идет с уменьшением энергии Гиббса. Величина энергии Гиббса одного моля раствора зависит от состава (рисунок 1.1)
Рисунок 1.1 - Энергия Гиббса бинарного раствора Пунктирная линия - энергия Гиббса системы из несмешивающихся компонентов А и В. Кривая линия - энергия Гиббса гомогенной системы, все ее точки лежат ниже прямой линии. Следствия из закона Рауля По закону Рауля давление растворителя над раствором всегда ниже, чем над чистым растворителем,
Осмотическое давление
Поясним понятие осмоса в растворах (рисунок 1.4). Поместим в сосуд (А) чистый растворитель. Трубка (В) заканчивается расширением. Широкий конец этой трубки закрывается полупроницаемой перегородкой (С). В трубку (В) наливается раствор до уровня жидкости в сосуде (А). Через полупроницаемую перегородку растворитель из сосуда (А) переходит в раствор в сосуде ( В ). Самопроизвольный переход растворителя через полупроницаемую перегородку в раствор называется осмосом. Частицы растворенного вещества через полупроницаемую перегородку перейти при этом не могут. Объем раствора в трубке (В) увеличивается. Через некоторое время подъем уровня раствора прекратится. Этому состоянию отвечает равенство двух противоположных сил: силе осмотического давления, способствующей всасыванию растворителя в раствор, и гидростатического давления столба жидкости (h), препятствующего осмосу.
Рисунок 1.4 – Простейший прибор для измерения осмотического давления А – внешний сосуд, В – внутренний сосуд, С – полупроницаемая мембрана
Если в сосуд (А) поместить раствор с концентрацией большей, чем в (В), то растворитель будет переходить из (В) в (А) (обратный осмос). Обратный осмос наблюдается и при создании давления в трубке В больше осмотического. При этом возникает миграция молекул растворителя из раствора в сосуд А. Этим методом опресняют морскую воду. Осмотическое давление зависит от концентрации растворенного вещества и температуры по уравнению Вант-Гоффа:
где Уравнение (1.4) справедливо для разбавленных растворов неэлектролитов. В растворах электролитов из-за диссоциации на ионы, число частиц будет больше, чем в растворах неэлектролитов, при тойже концентрации. Вследствие этого, осмотическое давление будет больше:
где i - изотонический коэффициент, i >1. Явление осмоса и осмотическое давление играют важную роль в жизнедеятельности живых и растительных организмов, в технологических процессах - везде, где есть полупроницаемые перегородки. Нормальное осмотическое давление клеточного сока у человека 7,5 -7,9 атм. Любое нарушение осмотического давления вызывает заболевание или свидетельствует о заболевании. В очаге воспаления осмотическое давление увеличивается до 15 -20 атм. Клетка, например, дрожжевая, помещенная в дистиллированную воду, будет набухать и станет упругой и эластичной. В некоторых случаях избыточная вода может привести к разрыву оболочки и гибели клетки (например, красные кровяные тельца гибнут при поступлении воды внутрь, происходит, так называемый, гемолиз). Если клетка помещена в концентрированный раствор, то происходит переход воды из сока клетки в раствор, обезвоживание клетки, сморщивание ее, так называемый, плазмолиз, который вызывает нарушение нормального течения физических и химических процессов. В процессе консервирования и сахар, и соль вызывают плазмолиз клетки микроорганизмов и, тем самым, обеззараживают систему. Кроме того, плазмолиз растительных клеток в растворе соли нарушает полупроницаемые клеточные оболочки. При этом выделяется клеточный сок, содержащий сахара, служащие основой молочно-кислого брожения. Полученная молочная кислота является антисептиком и придает специфический вкус продукту.
Реальные растворы Отклонения от закона Рауля В реальных растворах закон Рауля применим для растворителя лишь в бесконечно разбавленных растворах. В более концентрированных растворах за счет сил межмолекулярного взаимодействия наблюдаются отклонения от закона Рауля. а) Положительные отклонения Если
Положительные отклонения наблюдаются в системах: этанол - диэтиловый эфир; бензол - ацетон; кислород - азот и других. б) Отрицательные отклонения от идеального поведения характерны для растворов, компоненты которых взаимодействуют друг с другом сильнее, чем однородные молекулы, то есть εА-В > εА-А; εА-В > εВ-В. При этом возникают водородные связи, происходит сольватация, а иногда образуются химические соединения. Теплота при смешении выделяется, Такие отклонения наблюдаются в системах хлороформ - бензол; вода - серная кислота и других.
Рисунок 1.5 - Зависимость давления пара от состава раствора в реальных системах: а) положительные отклонения; б) отрицательные отклонения от закона Рауля
Иногда при одних соотношениях компонентов в растворе наблюдаются положительные отклонения, при других - отрицательные. Пример - раствор пиридина в воде (рисунок 1.6). Зависимость общего давления от состава жидкости в системах с отклонениями от закона Рауля будет также нелинейной (рисунки 1.5 и 1.6).
Рисунок 1.6 – Давление в системе пиридин – вода
В системах со значительными отклонениями от закона Рауля на диаграмме Робщ = f(Xж) возможно появление экстремума (минимума или максимума). Экстремум может появиться и при небольшом отклонении от идеального поведения, если давление пара над чистыми компонентами мало отличаются друг от друга, то есть
Рисунок 1.7 – Кривые общего давления с максимумом
Растворимость
Растворимость – это способность веществ образовывать гомогенные системы. Количественно она выражается в виде концентрации насыщенного раствора. Раствор считается насыщенным, если он находится в равновесии с избытком растворяемого вещества. Жидкие растворы могут быть образованы растворением в жидком растворителе твердого вещества, газа или жидкости.
Примеры решения задач Задача 1 50 г водного раствора FeCl2 с моляльностью 1,97 моль/кг с плотностью 1,332 г/см3 смешали со 150 мл 5 масс. % раствора FeCl2 с плотностью 1,038 г/см. Выразить состав полученного раствора всеми возможными способами. Дано: Раствор 1: Раствор 2:
b
b3 =? W 3 =? Х 3 =? Решение: Для каждого раствора найдем массу FeCl2 и Н20. Раствор 1: b
1251 г (р-ра) - 251г FeCl2; 50 г р-ра -
Итак, в растворе 1:
Раствор 2: m р.ра =r∙V = 1,038 ∙ 50 =156 г;
Раствор 3: m р-pa = 50 + 156 = 206 г; mH2O =40+ 148 = 188 г
b
Рассчитать молярную концентрацию нет возможности, поскольку неизвестна плотность полученного раствора.
Задача 2 При 100 °С тетрахлорэтилен имеет давление насыщенного пара 400 мм.рт.ст., а бромбензол - 196 мм.рт.ст.. Найти состав раствора, кипящего при 100 °С под давлением 360 мм.рт.ст., и состав насыщенного пара над раствором. Считать раствор идеальным. Дано:
t = 100 °С Pобщ = 360 мм.рт.ст.
Решение: Кипение наступает тогда, когда внешнее давление и давление насыщенного пара равны. Следовательно, 360 мм.рт.ст. - это и внешнее давление и общее давление насыщенного пара над раствором.
Задача 3 При 25 °С константа распределения иода между водой и амиловым спиртом равна 0,00435. Сколько граммов иода останется в трех литрах водного раствора (С = 1,3 г/л) после двухкратной экстракции амиловым спиртом, если всего израсходовано 400 мл спирта? Дано: К = 0,00435 =
п = 2 V = 3 л
Решение: Экстрагентом является амиловый спирт. Следовательно, данная константа распределения является обратной, требуемой в уравнении для расчета эффективности экстракции:
Рассчитываем константу распределения:
Масса растворенного иода в исходном растворе:
m = m0×x = 3,9 . 0,0037 = 0,014 г - масса иода, оставшегося в рафинате
Задача 4 Закрытый сосуд объемом 5,0 л содержит газ Н2S при температуре 20 0С и давлении равном 740 мм. рт. ст. Какой объем воды должен быть добавлен, чтобы парциальное давление Н2S понизилось до 500 мм. рт. ст.? Коэффициент абсорбции Н2S (α) равен 2,58.
Дано:
t1 = 20 0C T1 = T2 = 293 K P = 740 мм.рт.ст.= 0,984∙105 Па α = 2,58
Решение: Понижение давления происходит за счет растворения части Н2S в воде. Рассчитаем исходное количество Н2S и остаточное количество Н2S после растворения его в воде.
Пренебрежем изменением объема газа за счет добавления воды, то есть V2 = V1.
Рассчитаем количество Н2S, растворенное в воде:
Рассчитаем V0 – объем Н2S, приведенный к нормальным условиям (Р = 1,0133∙105 Па, Т = 273,15 К), который растворен в воде:
Задача 5 Метан плавится при температуре 90,5 К, его теплота плавления равна 70,7 Дж/моль. Определить растворимость метана в жидком азоте при температуре 50 К.
Дано:
Решение: Обычно мы знаем метан как газ, но в данном случае речь идет о твердом метане при температуре ниже его температуры плавления. Следовательно, надо найти растворимость твердого вещества в жидкости, что можно выполнить по уравнению Шредера:
Вопросы для самоконтроля 1. Смешение двух жидкостей сопровождается выделением теплоты и уменьшением объема. Какой тип отклонения от закона Рауля в данной системе? 2. Растворимость твердого вещества в жидкости является идеальной. Как изменится растворимость при понижении температуры? 3. Одинаковы ли величины осмотического давления КСl и сахара в воде, если их моляльности равны? 4. Изобразить диаграмму двух жидкостей в координатах (Ткип.- состав) для системы с положительным отклонением от закона Рауля, имеющей азеотроп состава х А = 0,5; причем 5. Система, состоящая из жидкостей А и В, имеет максимум на диаграмме (Ткип.- состав). Провести перегонку растворов с х А = 0,8 и х В = 0,8. Что отгоняется и что остается в кубе? 6. В какой воде – дистиллированной или морской – больше растворяется кислорода? 7. Какие из перечисленных веществ можно перегонять с водяным паром: С6Н6, NaCl,С2Н5ОН, СН3СООН, С6Н5NН2, С10Н8? 8. Коэффициент распределения иода между: водой и четыреххлористым углеродом - 0,0117; водой и сероуглеродом - 0,0017; водой и хлороформом - 0,0074. Каким из перечисленных экстрагентов наиболее эффективно извлекать иод из водного раствора? 9. Что называется термодинамической активностью?
ЭЛЕКТРОХИМИЯ
Числа переноса При прохождении электрического тока через раствор электролита катионы движутся к катоду, а анионы – к аноду. Благодаря разной подвижности катионы и анионы будут переносить неодинаковую часть тока. Доля электричества, перенесенная ионами одного вида, называется числом переноса иона. Обозначается t+ и t- - для катионов и анионов соответственно. Количество электричества, перенесенное ионами данного вида через единицу времени поверхности за 1 секунду, равно: для катионов q+ = z+ν+ CU+F, для анионов q- = z-ν- CU-F, где z+, z- - заряд ионов; ν+, ν- - число ионов; U+, U- - абсолютная скорость движения ионов; С – молярная концентрация электролита. Общее количество электричества равно сумме (q+ + q-). Тогда, согласно определению чисел переноса с учетом равенства z+ν+ = z-ν- (вследствие электронейтральности раствора), получаем выражение для чисел переноса:
Практически удобно рассматривать не целые ионы, а их части с зарядом, равным единице (например, Na +, ½ SО 42-). Тогда z+ и z- = 1; ν+ и ν- = 1; U+F = λ +; U-F = λ- - эквивалентные электропроводности катионов и анионов или подвижности ионов Очевидно, что t+ + t- = 1.
Кондуктометрия Измерение электрической проводимости – кондуктометрия широко применяется в лабораторной практике для определения физико-химических характеристик электролитов и растворов. Электродные процессы 2.3.1 Основные понятия и определения При погружении металлического электрода в раствор, содержащий ионы этого же металла, устанавливается равновесие на границе металл - раствор. Разность химических потенциалов в растворе и электроде приводит к тому, что электрод растворяется и посылает ионы в раствор, если Экспериментальному определению доступна лишь электрическая разность потенциалов между точками, которые находятся в одинаковых по химическому составу фазах. Если же точки расположены в различных по химическому составу фазах, то электрическую разность потенциалов измерить невозможно. Такой разностью потенциалов между электродом и раствором является гальвани-потенциал. Если же соединить два металлических электрода, погруженных в растворы, содержащие ионы этих металлов, тогда можно замерить разность потенциалов между этими электродами. При этом концы электрохимической цепи должны заканчиваться одинаковыми по своему составу металлами. Такая цепь называется правильно разомкнутой (рисунок 2.4).
Рисунок 2.4 - Правильно разомкнутые электрохимические цепи
На практике это обычно достигается простым подключением медных проводов к обоим электродам (рисунок 2.4 б). Электрохимическая цепь является равновесной, если процессы на электродах протекают бесконечно медленно. Разность потенциалов на концах правильно разомкнутой равновесной электрохимической цепи называется электродвижущей силой (ЭДС). Обозначается ЭДС - Е. Электрохимическую цепь можно представить схематически. Например:
Cu | Zn | ZnS04
Вертикальной сплошной чертой показывается наличие скачка потенциала на границе металл-металл, металл-раствор, а пунктирной - на границе двух растворов, так называемый диффузионный потенциал. Часто при записи цепи опускается повторение металла, предполагая, что цепь является правильно разомкнутой: Zn | ZnS04 Разность потенциалов Е на концах этой цепи складывается из четырех гальвани-потенциалов, каждый из которых отдельно замерен быть не может:
Рассмотрим, как определяется величина и знак ЭДС. Полезная работа обратимого процесса (в данном случае электрическая) равна убыли энергии Гиббса, то есть Для реакций, самопроизвольно протекающих в гальваническом элементе, (∆G < 0), ЭДС - положительна. Этому соответствует запись гальванического элемента так, чтобы правый электрод был более электроположителен, чем левый, движение электронов при этом происходит от левого электрода к правому, на котором и идет реакция восстановления. На положительном электроде идет реакция восстановления, на отрицательном - окисления. Электрод, на котором идет восстановление, называется катодом, а на котором идет окисление – анодом. В гальваническом элементе катод имеет положительный знак (в отличие от электролиза, где восстановление идет на отрицательном электроде, то есть катод будет отрицательным, см. раздел 2.4). ЭДС гальванического элемента можно рассчитывать по формуле Нернста: где Е0 - стандартная ЭДС цепи при активностях всех компонентов, равных единице; n - число электронов, участвующих в реакции; Так, для приведенной выше гальванической цепи, где протекает реакция
CuS04 + Zn →ZnS04 + Сu,
ЭДС можно рассчитать по уравнению (2.13):
Комбинируя различные электроды между собой, можно получить множество электрохимических цепей. Поскольку измерить гальвани-потенциал невозможно, то за величину, характеризующую процесс на отдельном электроде, принимают электродный потенциал. Электродным потенциалом называют ЭДС электрохимической цепи, построенной из стандартного водородного электрода и электрода окислительно - восстановительной полуреакции. Стандартный водородный электрод представляет собой платинированный платиновый электрод в растворе кислоты с активностью, равной единице, который омывается током водорода под давлением 1 атм. (1,013·105 Па), то есть a Н+ = 1;
При обозначении электрода водородный электрод не записывается, а подразумевается, и запись электрода выглядит так: CuSO4 | Cu, ZnSO4 | Zn. Знак электродного потенциала определяется знаком ЭДС при движении электронов от левого электрода (водородного) к правому. Если этот процесс самопроизволен, ∆G < 0, то Электродный потенциал нередко обозначается знаком Е. Мы принимаем обозначение Величины электродных потенциалов зависят от концентрации всех компонентов, участвующих в окислительно-восстановительной полуреакции. Зависимость эта выражается уравнением Нернста. Так, величина электродного потенциала Сu2+ |Сu равна ЭДС цепи, где протекает реакция: Н2 + Сu2+ → Сu + 2Н+. Учитывая, что
В общем случае уравнение Нернста для электродного потенциала имеет вид:
где аокисл, авосст - активности окисленных и восстановленных форм участников реакции. Если активности участников полуреакции равны единице, то ЭДС цепи типа (А) и (В) будет называться стандартным электродным потенциалом. Величина потенциала стандартного водородного электрода равна нулю. Классификация электродов В зависимости от природы веществ, участвующих в электродной реакции, электроды делятся на две группы: 1. Электроды, образованные электрохимически активными металлами, участвующими в токообразующей реакции. 2. Электроды с инертными металлами, не участвующими в токообразующей реакции. К первой группе относятся электроды первого и второго рода. Электроды первого рода - системы, состоящие из металла, опущенного в раствор соли этого металла. Например: Ag+ | Ag; Sn2+ | Sn. Реакции, протекающие на электродах: Ag+ + e Sn2+ + 2e Потенциал рассчитывается по уравнению (2.14)
К электродам первого рода также относятся амальгамные электроды и электроды, образованные сплавами, в которых меняется активность металла. Амальгама – металлическая система, одним компонентом которой является ртуть. Это, в основном, твердые растворы, химические соединения, жидкие растворы. Например:
Здесь электродный потенциал зависит также и от активности металла в амальгаме. К электродам второго рода относят металлические электроды, покрытые труднорастворимым соединением этого металла (солью, гидроксидом или оксидом), погруженные в раствор, содержащий анионы этой соли или ионы ОН- или Н+ (в случае гидроксида или оксида). Восстановление металла в этом случае идет из соли, оксида или гидроксида. При записи электрода вещества, из которых состоит электрод, записываются через запятую. Раствор отделяется вертикальной чертой, показывающей наличие скачка потенциала.
В случае оксидно - металлических электродов (б, в, г) электродный потенциал зависит от рН раствора. Ко второй группе относятся окислительно - восстановительные и газовые электроды. Газовые электроды состоят из инертного металла (часто платины), к которому подводится электрохимически активный газ. Молекулы газа адсорбируются на поверхности металла, распадаясь на атомы, которые и участвуют в электродном процессе. Платина с адсорбированным газом частично погружена в раствор, содержащий ионы этого газа. Примерами таких электродов могут служить водородный, хлорный, кислородный. Водородный электрод в кислой среде:
Н+ | H2, Pt; Н+ + е
Водородный электрод в щелочной среде: ОН-│H2, Pt 2Н2О + 2е
Кислородный электрод, в отличие от водородного электрода, является необратимым. Кислородный электрод в кислом растворе:
Кислородный электрод в нейтральном или щелочном растворах
Уравнения для Окислительно-восстановительные (редокс) электроды. Это электроды, составленные из инертного металла (обычно платины), погруженного в раствор, где присутствуют ионы какого-либо вещества, имеющие различную степень окисления. В этом случае реакции окисления – восстановления идут без образования новой фазы. Множество разнообразных редокс-электродов можно разделить на два класса: а) не зависящие от рН раствора. К ним относятся некоторые неорганические окислительно – восстановительные системы: Fe3+, Fe2+ | Pt Fe3+ + e → Fe2+
б) зависящие от рН раствора. К этой группе относятся часть неорганических и все органические системы. Н+, MnO4-, Mn2+ | Pt MnO4- + 8H+ + 5e → Mn2+ + 4H2O H+, HCOOH, HCOH | Pt HCOOH+2H+ + 2e → HCOH + H2O
Диффузионный потенциал На границе двух растворов электролитов произвольного состава возникает скачок потенциала, называемый диффузионным потенциалом. Причиной его возникновения является различная подвижность ионов в растворах. Рассмотрим два наиболее простых случая. 1) Граница растворов одного и того же электролита с различной концентрацией.
2) Граница растворов различных электролитов с одинаковой концентрацией.
где По этим формулам рассчитывается численное значение φдифф, но не его знак. Выбор знака φдифф зависит от взаимного направления полей: 1) на границе двух растворов; 2) электродов. Если направление полей совпадает, то φдифф > 0; если не совпадает, то φдифф < 0 (смотри раздел 2.5 задачи 4, 5). На практике для того, чтобы снизить величину φдифф до
|
||||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 201; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.146.206.87 (0.011 с.) |


 <
<  . Это приводит к повышению температуры кипения раствора и понижению температуры замерзания растворителя из раствора нелетучего компонента по сравнению с соответствующими температурами для чистого растворителя.
. Это приводит к повышению температуры кипения раствора и понижению температуры замерзания растворителя из раствора нелетучего компонента по сравнению с соответствующими температурами для чистого растворителя.
 , (1.4)
, (1.4) - осмотическое давление, Па; С - концентрация растворенного вещества в растворе, моль/м3; R - газовая постоянная, Дж/(моль×К); Т - температура, К.
- осмотическое давление, Па; С - концентрация растворенного вещества в растворе, моль/м3; R - газовая постоянная, Дж/(моль×К); Т - температура, К. ,
,
 ;
;  >
>  > 0 (объем увеличивается), а
> 0 (объем увеличивается), а 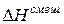 > 0 (тепло поглощается). При этом за счет ослабления сил взаимодействия выход молекул в паровую фазу облегчается и давление пара над реальным раствором становится больше, чем над идеальным:
> 0 (тепло поглощается). При этом за счет ослабления сил взаимодействия выход молекул в паровую фазу облегчается и давление пара над реальным раствором становится больше, чем над идеальным: >
>  ,
,  >
>  .
. < 0; выход молекул в пар затрудняется и
< 0; выход молекул в пар затрудняется и  <
<  ,
,  <
< 
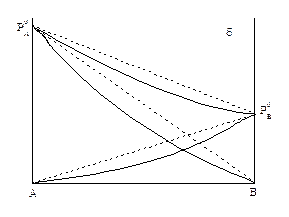

 (рисунок 1.7).
(рисунок 1.7).
 =50r
=50r  = 150 мл
= 150 мл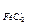 =1,97моль/кг
=1,97моль/кг 
 = 1,332 г/см3
= 1,332 г/см3  = 1,038 г/см3
= 1,038 г/см3 = l,97×M FeCl2 = 1,97∙127,5 =251 г;
= l,97×M FeCl2 = 1,97∙127,5 =251 г; 
 = 1000 г; mp.pa= 1251 г
= 1000 г; mp.pa= 1251 г г.
г.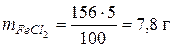



 =400 мм.рт.ст.
=400 мм.рт.ст.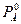 = 196 мм.рт.ст.
= 196 мм.рт.ст.


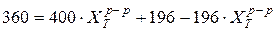
 ;
; 


 =1,3г/л
=1,3г/л = 400/2 = 200 мл = 0,2 л
= 400/2 = 200 мл = 0,2 л =?
=?

 - доля иода, оставшегося в рафинате.
- доля иода, оставшегося в рафинате.
 = 5,0 л = 5,0∙10-3 м3
= 5,0 л = 5,0∙10-3 м3 -?
-?




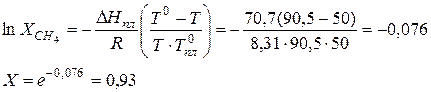
 >
>  .
.

 ;
;  .
. >
>  . Если же
. Если же 
 CuS04 | Cu
CuS04 | Cu

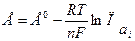 , (2.13)
, (2.13)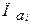 - произведение активностей всех участников окислительно-восстановительной реакции в гальваническом элементе с учетом стехиометрических коэффициентов, которые для исходных веществ берутся со знаком «минус», а для продуктов со знаком «плюс».
- произведение активностей всех участников окислительно-восстановительной реакции в гальваническом элементе с учетом стехиометрических коэффициентов, которые для исходных веществ берутся со знаком «минус», а для продуктов со знаком «плюс». .
. . При записи cхемы гальванического элемента стандартный водородный электрод всегда располагается слева.
. При записи cхемы гальванического элемента стандартный водородный электрод всегда располагается слева.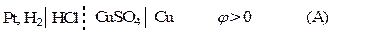

 > 0, значит и
> 0, значит и  > 0.
> 0. , чтобы различать электродный потенциал и ЭДС суммарной цепи.
, чтобы различать электродный потенциал и ЭДС суммарной цепи. а
а  = 1; а
= 1; а  = 1, получим:
= 1, получим:
 , (2.14)
, (2.14) Ag
Ag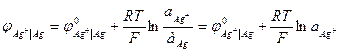 , так как активность чистого твердого вещества равна единице.
, так как активность чистого твердого вещества равна единице.


 ;
;


 .
.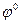 = 0 при а Н+ = 1 и рН = 0.
= 0 при а Н+ = 1 и рН = 0.
 В при а ОН- = 1 и рН = 14.
В при а ОН- = 1 и рН = 14.
 (при РО2 = 1)
(при РО2 = 1) В при а Н+ = 1 и рН = 0
В при а Н+ = 1 и рН = 0

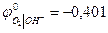 В при а ОН- = 1 и рН = 14
В при а ОН- = 1 и рН = 14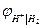 и
и  термодинамически идентичны. Идентичны и уравнения для
термодинамически идентичны. Идентичны и уравнения для 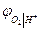 и
и  . Это объясняется термодинамической зависимостью активностей
. Это объясняется термодинамической зависимостью активностей  и
и  через константу диссоциации воды
через константу диссоциации воды  (ионное произведение воды).
(ионное произведение воды).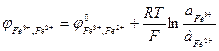

 , где a 1 > a 2;
, где a 1 > a 2; ,
,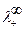 и
и  - предельные подвижности ионов одного электролита;
- предельные подвижности ионов одного электролита; 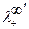 и
и  - предельные подвижности ионов другого электролита.
- предельные подвижности ионов другого электролита.


