
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Влияние температуры на скорость реакции. Энергия активацииСодержание книги
Поиск на нашем сайте
В общем случае скорость химической реакции с повышением температуры увеличивается. Поскольку
Если известны константы скорости при температурах, отличающихся не на 10 К, то коэффициент Вант-Гоффа может быть определен из уравнения:
где k2 и k1 – константы скорости при температурах Т2 и Т1.
Более строгую зависимость константы скорости от температуры дает уравнение:
которое получило название уравнения Аррениуса. Величина Е имеет размерность энергии и носит название энергии активации. Энергию активации можно определить как тот избыток энергии по сравнению со средней энергией молекул при данной температуре, которым должны обладать молекулы, чтобы они могли легко вступить в химическую реакцию. Поскольку Е > 0, то производная Связь энергии активации с тепловым эффектом можно проиллюстрировать с помощью представления об энергетическом барьере (рисунок 3.6). Химическую реакцию можно представить как переход системы из энергетического состояния 1 в состояние 2, сопровождающееся тепловым эффектом В задачу химической кинетики входит поиск способов уменьшения энергетического барьера, энергии активации, для увеличения скорости. Одним из таких способов является применение катализатора. При осуществлении реакции в прямом направлении выделяется количество энергии Уравнение (3.6) легко проинтегрировать. Считая, что
где lnA – константа интегрирования.
Отсюда видно, что величинами, характеризующими реакцию, являются предэкспоненциальный множитель А и энергия активации Е.
Рисунок 3.6 – Диаграмма, иллюстрирующая связь Е и
Поскольку для вступления в химическую реакцию молекулы должны обладать некоторой избыточной энергией (Е) по сравнению со средней величиной (рисунок 3.7), то влияние повышения температуры на рост скорости реакции можно объяснить увеличением числа частиц, обладающих этим избытком энергии. Обратимся к рисунку 3.7, где изображена зависимость величины
Рисунок 3.7 – Кривая распределения молекул по энергиям
Площадь под кривой правее абсциссы Величину энергии активации можно определить двумя методами. Первый метод – графический, с использованием уравнения Аррениуса в виде (3.7):
Если построить график зависимости экспериментальных величин ln k от 1/Т, то получим прямую. По оси ординат отсекается отрезок, равный lnA. Тангенс угла наклона на кривой равен
Рисунок 3.8 – Зависимость логарифма константы скорости химической реакции от обратной температуры
Второй метод основан на измерении скорости химической реакции при двух температурах. Для этого из уравнения (3.6) получим:
Постоянной энергия активации может быть только в простых реакциях. Для сложных реакций величина Е является переменной и не имеет такого простого физического смысла, как в случае простых реакций. Тем не менее, и в этом случае, принято величину Е называть энергией активации, но определяют ее из дифференциального уравнения Аррениуса Для сложных реакций, следовательно, не будет линейной зависимости
3.4 Методы определения порядка реакции
Для определения порядка реакции в целом необходимо определить частные порядки по каждому веществу, вступающему в реакцию, а затем суммировать их. Для определения порядка по данному веществу необходимо создать условия, при которых будет изменяться концентрация только этого вещества.
Укажем некоторые из таких условий: 1. В реакции принимает участие одно исходное вещество. 2. Скорость реакции зависит от концентрации одного реагента и катализатора, а концентрация катализатора постоянна по ходу реакции. 3. Все реагенты, кроме одного, берутся в большом избытке, в результате чего их концентрации мало меняются по ходу реакции и могут рассматриваться как постоянные. 4. Концентрация всех реагентов, кроме одного, поддерживается постоянной каким-либо искусственным путем. Например, проводя реакции с участием иона ОН - как реагента, можно обеспечить присутствие буфера для поддержания концентрации ОН -. При определении порядка реакции используется основное свойство кинетического уравнения
Метод подстановки
По ходу реакции определяют текущие концентрации исходного вещества в различные моменты времени от начала реакции. Предполагают, что реакция первого порядка. По уравнению для константы скорости первого порядка (раздел 3.2.2, с. 78) рассчитывают все возможные значения К. Если значения К постоянны (в пределах ошибки опыта), то реакция имеет первый порядок. Если же не постоянны значения К, или закономерно убывают или возрастают, то реакция не первого порядка. Аналогично проверяют на второй порядок. Если реакция не первого и не второго порядка, то для определения порядка используют другие методы.
Графический метод
Этот метод основан на том, что кинетическая кривая может иметь линейный вид (x) = f(t), где вид (x) соответствует конкретному порядку реакции: для первого порядка ln C = f (t), для второго порядка 1/С = f (t), для третьего порядка 1/С2 = f (t), для нулевого порядка Спродукта = f (t). Поочередно строя такие зависимости, смотрят, в каких координатах получается прямая линия. Этот метод и метод подстановки взаимосвязаны, и нет смысла его использовать, если метод подстановки не выявил порядок реакции.
Метод начальных скоростей
Скорость расходования вещества в начальный момент времени определяется по уравнению:
Для понижения порядка проводят ряд опытов, в которых берется вещество А с различной начальной концентрацией,
Получилось уравнение прямой в координатах ( Порядок реакции можно приблизительно определить по значениям двух начальных скоростей (
Вычитая второе уравнение из первого, получаем Для приближенного расчета скоростей можно использовать соотношение: где
Метод избытка (метод Вант - Гоффа)
Это метод определения порядка по изменяющейся во времени скорости реакции от концентрации реагента. Реакцию проводят при большом избытке всех реагентов, кроме одного, например А. Тогда
В процессе реакции расходуется реагент и уменьшается скорость реакции. Скорости реакции находят из полной кинетической кривой, проводя графическое дифференцирование, определяя тангенсы углов наклона касательных к кинетической кривой (рисунок 3.9).
Рисунок 3.9 – Графическое дифференцирование кинетической кривой
Рисунок 3.10 – Определение порядка реакции
По найденным значениям u строят график в координатах (
|
|||||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 195; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.110.76 (0.009 с.) |

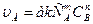 , то влияние температуры на скорость выражается через влияние температуры на k, поскольку концентрация от температуры практически не меняется. Опыт показывает, что при повышении температуры на 10 К скорость реакции возрастает в 2…4 раза (правило Вант-Гоффа). Для характеристики зависимости скорости химической реакции от температуры был выведен температурный коэффициент скорости реакции:
, то влияние температуры на скорость выражается через влияние температуры на k, поскольку концентрация от температуры практически не меняется. Опыт показывает, что при повышении температуры на 10 К скорость реакции возрастает в 2…4 раза (правило Вант-Гоффа). Для характеристики зависимости скорости химической реакции от температуры был выведен температурный коэффициент скорости реакции: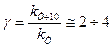 .
.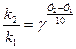 ,
,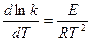 , (3.6)
, (3.6) >0 следовательно, ln k и k будут всегда возрастать с ростом Т.
>0 следовательно, ln k и k будут всегда возрастать с ростом Т. (при Р = const). Из рисунка 3.6 видно, что переход из состояния 1 в состояние 2 возможен при затрате энергии Е, а обратный переход возможен при затрате энергии Е´. Поскольку Е´ > Е, то энергетический барьер обратной реакции будет больше, чем прямой. Следовательно скорость обратной реакции будет меньше скорости прямой.
(при Р = const). Из рисунка 3.6 видно, что переход из состояния 1 в состояние 2 возможен при затрате энергии Е, а обратный переход возможен при затрате энергии Е´. Поскольку Е´ > Е, то энергетический барьер обратной реакции будет больше, чем прямой. Следовательно скорость обратной реакции будет меньше скорости прямой. , а в обратном направлении затрачивается такое же количество энергии, что выделяется в прямом.
, а в обратном направлении затрачивается такое же количество энергии, что выделяется в прямом. , получим
, получим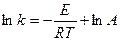 , (3.7)
, (3.7) .
.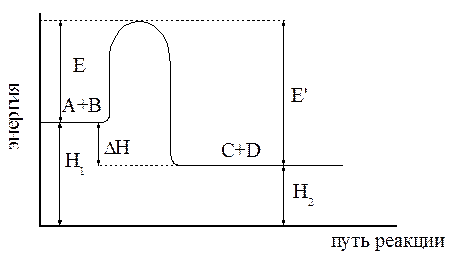
 от энергии, так называемая кривая распределения молекул по энергиям. Где dN – число молекул, обладающих энергиями от
от энергии, так называемая кривая распределения молекул по энергиям. Где dN – число молекул, обладающих энергиями от 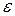 до
до  ; N0 – общее число молекул. Пусть
; N0 – общее число молекул. Пусть  - энергия, превышающая среднюю на энергию активации.
- энергия, превышающая среднюю на энергию активации.
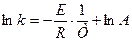 .
.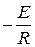
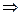


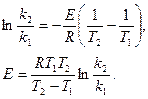
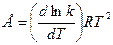 , используя зависимость
, используя зависимость 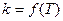 и
и 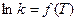 .
.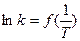 .
.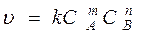 , согласно которому константа скорости и порядок реакции по ее компонентам остаются постоянными в течение всей реакции, а так же при изменении начальных концентраций реагентов.
, согласно которому константа скорости и порядок реакции по ее компонентам остаются постоянными в течение всей реакции, а так же при изменении начальных концентраций реагентов. .
. , а начальная концентрация B во всех опытах берется одинаковой. Тогда
, а начальная концентрация B во всех опытах берется одинаковой. Тогда , где
, где  ,
,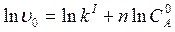 . (3.8)
. (3.8) ) с тангенсом угла наклона, равным порядку реакции, n. Для определения начальных скоростей получают начальные участки кинетических кривых, поскольку лишь в начале реакции сохраняется постоянство концентрации вещества В.
) с тангенсом угла наклона, равным порядку реакции, n. Для определения начальных скоростей получают начальные участки кинетических кривых, поскольку лишь в начале реакции сохраняется постоянство концентрации вещества В. ), которые соответствуют двум начальным концентрациям реагента (
), которые соответствуют двум начальным концентрациям реагента (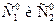 ), используя соотношение (3.8):
), используя соотношение (3.8):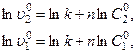
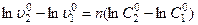 откуда
откуда  .
. ,
,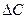 - изменение концентрации реагента за промежуток времени
- изменение концентрации реагента за промежуток времени  .
.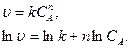
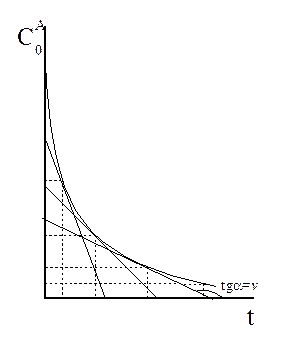

 ), согласно уравнению (3.8), и находят порядок, n (рисунок 3.10).
), согласно уравнению (3.8), и находят порядок, n (рисунок 3.10).


