
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дифференцирующие линейные цепиСодержание книги
Поиск на нашем сайте
Простейшая дифференцирующая цепочка представляет собой делитель напряжения, у которого роль верхнего плеча делителя выполняет конденсатор С (рис.2.5, а), с сопротивлением ZC = 1/wC. Вместе с источником сигнала и нагрузкой дифференцирующая цепочка примет вид (рис.2.5, б). Выходное напряжение такого делителя без учета внутреннего сопротивления источника сигнала описывается выражением:
Рисунок 2.5 − Дифференцирующая линейная цепочка
Анализ выражения (2.16) показывает, что при w = 0, ZC=¥, коэффициент передачи такого частотно-зависимого делителя напряжения КДН = 0,выходное напряжение Uвых будет равно нулю, но по мере роста частоты входного сигнала КДН начинает увеличиваться. На АЧХ (рис.2.6) это увеличение составляет 20 dB/дек.
Рисунок 2.6 – АЧХ дифференцирующей линейной цепочки
При частоте w = ¥, ZC становится равным нулю, т.е. верхнее сопротивление делителя превращается в закоротку, Uвых = Uвх. Такая цепочка получила название фильтра верхних частот (ФВЧ). ФВЧ предназначен для передачи без изменения сигналов высоких частот, а на нижних частотах обеспечивает затухание сигналов и опережение их по фазе относительно входных сигналов. Амплитудно-частотная и фазо-частотная характеристики такой цепи описываются уравнениями:
Фазовый сдвиг на частоте среза составляет +450 . А частота среза вычисляется по той же формуле, что и для интегрирующей цепи: fср=1/ 2 πRC. Как и для фильтра нижних частот, АЧХ фильтра верхних частот можно составить из двух асимптот (рис.2.6): 1. К (w) = 1 в области высоких частот, при f>>fср. 2. К (w) » wRC на низких частотах при f<<fср. Коэффициент передачи схемы пропорционален частоте входного сигнала, наклон АЧХ составляет 20 dB/дек. 3. Если f = fср, то K (w)= 1/ Рассмотрим физические процессы при воздействии на электрическую цепочку напряжением типа прямоугольного импульса. При нулевых начальных условиях (конденсатор разряжен) скачек напряжения на входе инициирует процесс заряда конденсатора по цепи:
Изменение выходного сигнала для этого случая при амплитуде входного импульса Umax в течение длительности импульса tи происходит по экспоненциальному закону
Переходные процессы для различных значений τ показаны на рис. 2.6, б. Очевидно, если соблюдается условие tи << τ, то RС -цепь передает импульс практически без искажений, поскольку за время прохождения импульса конденсатор зарядиться не успевает. Чем ближе значения tи и τ, тем большие искажения претерпевает импульс. Если tи >> τ, то RС -цепь работает как дифференцирующая с тем большей точностью дифференцирования, чем лучше соблюдается это условие. Разделительные цепи не должны пропускать постоянную составляющую входного напряжения, которая имеется в любой однополярной импульсной последовательности, тогда как переменная составляющая должна передаваться без заметных искажений. Отсюда необходимо выбирать постоянную времени τ разделительной цепи, значительно превышающую длительность импульса. Так, для относительного спада импульса менее 1% необходимо выбрать τ разделительной цепи, по крайней мере в 100 раз больше tu. Укорачивающие (в некоторых устройствах они выполняют функцию форсирующих) цепи применяются для формирования коротких разнополярных импульсов с длительностью, меньшей длительности входных импульсов. Длительность выходных импульсов при прямоугольном входном импульсе определяется только постоянной времени τ цепи, величина которой определяется исходя из требуемой длительности импульса.
При расчете разделительной цепи для устройства, передающего последовательность импульсов необходимо учитывать ряд особенностей. Для примера рассмотрим цепь, у которой τ >> tи. Пусть на такую разделительную цепь поступают однополярные прямоугольные импульсы длительностью tи спериодом следования Т (рис. 2.7).
Рисунок 2.7 – Однополярные прямоугольные импульсы
Пусть к приходу первого импульса напряжение на конденсаторе равно нулю: UC (0) = 0 (нулевые начальные условия). Физические процессы, которые происходят с приходом первого импульса, были уже рассмотрены (см. рис.2.6, а). По истечении времени первой паузы tn = Т − tи на вход поступает точно такой же второй импульс. Начальные условия для него будут ненулевыми, так как UC (T) ≠ 0, и за время длительности второго импульса напряжение на конденсаторе возрастает до большей величины, чем это было при первом импульсе. При этом амплитуда выходных импульсов уменьшается на величину UC, и появляются отрицательные импульсы. Наблюдается «сползание» импульсов в область отрицательных значений. Процесс установления режима работы RС - цепи будет завершенным, когда приращение заряда на обкладках конденсатора С за время импульса q (tи) станет равным уменьшению его за время паузы q (tп). При этом напряжение на конденсаторе изменяется относительно среднего значения Uср.
Полосовые фильтры
Интегрирующее и дифференцирующее звенья при воздействии на них непрерывными случайными сигналами ведут себя как, соответственно, фильтры нижних и верхних частот, АЧХ которых представлены на рис. 2.4 и 2.6. Последовательно соединив два этих фильтра, можно получить фильтр, пропускающий сигналы, лежащие в заданной полосе. Такой фильтр называют полосовым (рис. 2.8).
Рисунок 2.8 – Полосовой фильтр
Элементы R 1 и C 2 образуют фильтр нижних частот, а C 1 и
фазо-частотная характеристика
График АЧХ приведен на рис.2.4.2. Максимальный коэффициент усиления K(w) имеет место при wRC = 1, резонансная частота fр равна
Фазовый сдвиг на резонансной частоте равен нулю, а коэффициент передачи K р = 1/3.
Рисунок 2.9 – АЧХ полосового фільтра Как следует из рисунка, уменьшение и увеличение частоты входного сигнала относительно fр вызывает уменьшение коэффициента передачи вплоть до нуля. К недостаткам такого фильтра относят малый коэффициент передачи на резонансной частоте (1/3).
Зависимости К (w) и φ (w) от частоты имеют вид (рис. 2.11)
Рисунок 2.11 – АЧХ на частоте резонанса полосового фильтра
Недостатком моста Вина является низкий коэффициент передачи (1/3) и отсутствие общей точки между входом и выходом, что затрудняет съем сигнала с выхода фильтра.
Амплитудно и фазочастотные характеристики двойного
Рисунок 2.13 – АЧХ двойного Т-образного моста
Если необходимо получить лучшие характеристики фильтров по сравнению с однозвенными, например, более быстрое уменьшение коэффициента передачи фильтра, можно включить n фильтров нижних частот последовательно. Передаточная функция такой системы
где а 1, a 2,..., аn − действительные положительные коэффициенты, P=p/wcp − нормированная комплексная переменная. Уменьшение коэффициента передачи такого фильтра характеризуется величиной 20 дБ на каждую декаду. Корни передаточной функции (2.27) являются отрицательными и действительными, что отвечает характеристикам RС-фильтров n - го порядка. Передаточная функция фильтра нижних частот в общем виде может быть записана как
где С1,С2,...,Сn − положительные действительные коэффициенты. Порядок фильтра определяется максимальной степенью переменной P. Для реализации фильтра необходимо разложить полином знаменателя на множители. Если среди корней полинома есть комплексные, то выражение (2.27) не может быть использовано, а его следует записать в виде произведения сомножителей второго порядка:
где ai, bi − положительные действительные коэффициенты, причем для нечетных порядков полинома b 1 равен нулю. Такие многозвенные фильтры имеют достаточно сложные полиномиальные характеристики, для аппроксимации которых используют несколько типовых полиномов: Баттерворта, Чебышева, Бесселя. В соответствии с этими полиномами аппроксимируемые ими фильтры называются фильтрами Баттерворта, Чебышева, Бесселя. Фильтры Баттерворта обеспечивают длинный горизонтальный участок АЧХ (рис. 2.14, кривая 2) в полосе пропускания и резкий спад ее за частотой среза. Переходная характеристика такого фильтра при ступенчатом входном сигнале имеет колебательный характер, причем с увеличением порядка фильтра (числа звеньев) колебания усиливаются. Фильтры Чебышева имеют более круто спадающую характеристику за частотой среза, однако в полосе пропускания она не монотонна, а имеет волнообразный характер с постоянной амплитудой колебаний.
Рисунок 2.14 – АЧХ Фильтры Баттерворта
При заданном порядке фильтра более резкому спаду АЧХ за частотой среза соответствует большая неравномерность в полосе пропускания. Переходная характеристика h (t) является колебательной, причем с ростом порядка фильтра колебания увеличиваются. Колебательность h (t) фильтра Чебышева больше, чем фильтра Баттерворта. Фильтры Бесселя (кривая 1) имеют более пологий спад АЧХ по сравнению с фильтрами Баттерворта и Чебышева, однако обладают оптимальной переходной характеристикой. Переходный процесс на выходе этого фильтра при ступенчатом возмущении практически не имеет колебаний. Фазовый сдвиг выходного сигнала пропорционален частоте входного сигнала. Амплитудно-частотные характеристики трех рассмотренных фильтров нижних частот четвертого и десятого порядков показаны на рис. 2.14 и 2.15. Можно заметить, что характеристика фильтра Чебышева (кривая 3) имеет наиболее крутой спад для частот входного сигнала, превышающих частоту среза, но заметную неравномерность в полосе пропускания. Переходные процессы этих фильтров имеют большую амплитуду колебаний при ступенчатом входном сигнале.
Рисунок 2.15 − Амплитудно-частотные характеристики фильтров нижних частот десятого порядков
Переходный процесс для фильтра Бесселя практически не имеет колебаний. С помощью одной и той же схемы можно получить характеристики фильтра любого типа определенного порядка, изменяя лишь номиналы соответствующих резисторов и конденсаторов. Чтобы рассчитать схему конкретного фильтра, следует знать его частотные характеристики при заданном его порядке. Параметры элементов фильтра непосредственно связаны с коэффициентами аi и bi аппроксимирующей его полиномиальной функции, которые должны иметь строго определенные значения. Корни этих полиномов могут иметь сопряженные комплексные значения, что приводит к невозможности реализации такого фильтра с помощью пассивных RС-цепей. Для реализации фильтров с сопряженными комплексными корнями могут быть использованы LRC-фильтры. Однако для низких частот нужны большие индуктивности, которые сложны в изготовлении и обладают плохими электрическими характеристиками. Применения индуктивностей можно избежать, используя RС-схемы с активными элементами (например, операционными усилителями). Такие схемы называются активными фильтрами.
Используя логарифмическое представление, можно перейти от нижних частот к верхним, зеркально отобразив АЧХ относительно частоты среза, т.е. заменив wRС на 1/wRС. При этом частота среза остается без изменений, а K 0 переходит в K¥. Наряду с RC - фильтрами для обработки электрических сигналов можно использовать RLиRLC фильтры (рис. 2.16). Однако применение индуктивностей в фильтрах имеет ряд особенностей.
Рисунок 2.16 − RLиRLC фильтры
К сожалению, производство катушек индуктивности и импульсных трансформаторов не поддается микроминиатюризации, что исключает их широкое применение в современной микромощной РЭА. Кроме того, индуктивности создают вокруг себя переменное магнитное поле, что требует дополнительных мер по обеспечению помехоустойчивости РЭА. Однако в сильноточных цепях, например в фильтрах питания, где токи составляют от единиц до сотен ампер, RLфильтр успешно конкурирует с RC, для которого размеры и вес конденсаторов становятся непозволительно велики. Контрольные вопросы
1. Как изменяется форма напряжения на выходе дифференцирующей цепи, если изменять сопротивление, емкость цепи, длительность и период повторения прямоугольных импульсов на входе? 2. Запишите формулу для определения длительности импульса на выходе дифференцирующей цепи, если на ее вход воздействует импульс прямоугольной формы. 3. Объясните физические процессы, происходящие в дифференцирующей цепи при воздействии на нее прямоугольных импульсов напряжения. 4. Определите форму напряжения на выходе интегрирующей цепи, если ее входе импульс треугольной формы. 5. Изобразите форму напряжения на выходе дифференцирующей цепи при воздействии на ее вход последовательности прямоугольных импульсов, где длительность импульсов больше длительности паузы. 6. Определите форму напряжения на выходе дифференцирующей цепи, если на ее входе импульсы треугольной, трапецеидальной, пилообразной формы, импульсы с экспоненциальным фронтом и срезом. 7. Как изменяется реакция на выходе цепи при изменении длительности фронта, амплитуды пульса, постоянной времени цепи? 8. Как влияет на форму выходного импульса дифференцирующей цепи выходное сопротивление генератора импульсов? 9. Объясните физические процессы, происходящие в интегрирующей цепи при воздействии на ее вход прямоугольных импульсов. 10. Какой делитель напряжения обладает самой широкой полосой пропускания? 11. Как будет изменяться форма выходного сигнала интегрирующей цепи, если изменить сопротивление цепи, емкость, длительность и период повторения входных импульсов? 12. Как влияет на форму выходных импульсов RС-цепи сопротивление нагрузки, подключаемое параллельно конденсатору С, паразитная емкость, выходное сопротивление генератора импульсов? 13. Какая цепь вызывает искажение плоской вершины импульса? 14. Какие искажения формы прямоугольного импульса вызывает интегрирующая цепь. Электронные усилители
|
|||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 308; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.227.49.94 (0.008 с.) |

 . (2.16)
. (2.16) , (2.17)
, (2.17)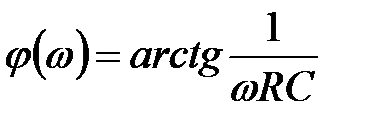 . (2.18)
. (2.18) , что соответствует затуханию на 3 дБ.
, что соответствует затуханию на 3 дБ.  (2.19)
(2.19) , (2.20)
, (2.20) (2.21)
(2.21) (2.22)
(2.22) , (2.23)
, (2.23) , при wRC ≠1. (2.24)
, при wRC ≠1. (2.24) , (2.25)
, (2.25) , при wRC ≠1. (2.26)
, при wRC ≠1. (2.26)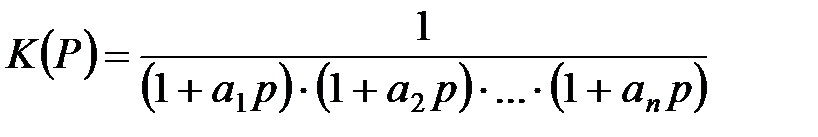 , (2.27)
, (2.27) , (2.28)
, (2.28)
 , (2.29)
, (2.29)


