
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Частотно-независимый делитель напряженияСодержание книги
Поиск на нашем сайте
Частотно-независимый делитель напряжения (ДН) предназначен для уменьшения напряжения источника сигнала до требуемой величины. ДН применяется для согласования входного каскада с источником сигнала по напряжению, для задания рабочей точки транзистора в усилителе, для формирования эталонного (чаще говорят «опорного») напряжения. Схема простейшего делителя напряжения приведена на рис.2.1.
Рисунок 2.1 – Схема простейшего делителя напряжения
В идеальном случае Rг = 0; Rн = ¥. Поэтому Uвх = Ег; Rвх = R1+ R2;
где К ДН − коэффициент передачи ДН.
Из выражения (2.1) видно, что выходное напряжение ДН может принимать любые значения от нуля до Ег. Величина UВЫХ не зависит от абсолютных значений R1 и R2, а зависит только от отношения (2.2). Амплитудно-частотная характеристика ДН представляет собой прямую, параллельную оси частот. При анализе реальных электронных схем, для исключения грубых ошибок, всегда необходимо учитывать электрические характеристики источника сигнала и нагрузки. Важнейшими из них являются: - величина и полярность э.д.с. источника сигнала; - внутреннее сопротивление источника сигнала (на рис. 2.1 – Rг); - АЧХ и ФЧХ источника сигнала; - сопротивление нагрузки (на рис. 2.1 – Rн); - значения паразитных емкости и индуктивности нагрузки и др. Из рисунка видно, что с учетом внутреннего сопротивления источника сигнала входное напряжение ДН равно:
Из чего следует, что только часть напряжения сигнала падает на ДН, а другая часть падает на внутреннем сопротивлении источника. И чем больше Rг относительно суммы R1+R2, тем большая часть сигнала падает на Rг, что снижает к.п.д. источника. Cчитаются приемлемыми потери на Rг, не превышающие 10%. Следовательно, зная Rг, можно определить граничное значение входного сопротивления делителя из неравенства
R1+R2³10Rг. (2.4) Очевидно, сумма сопротивлений R1+R2+Rг задает максимальное значение тока источника сигнала: Iгmax = Uг/R1+R2+Rг (без учета сопротивления нагрузки). Величина выходного напряжения ДН определяется из допустимого значения напряжения для нагрузки. Из рисунка видно, что Rн включается параллельно R2. Если Rн = ¥, выходное напряжение равно:
Однако в реальных устройствах Rн имеет конечное значение (для большинства электронных устройств Rн находится в интервале от 100 Ом до 1 МОм).
У многих электронных устройств (ЭУ) его входное сопротивление - переменная величина, которая, как правило, включает в себя переменное сопротивление перехода база-эмиттер транзистора. Значение сопротивления этого перехода зависит от величины и полярности входного напряжения и от его температуры. Поэтому даже для одного и того же устройства входное сопротивление может лежать в широких пределах. Rн для ДН может быть входным сопротивлением ЭУ. Это, в свою очередь, накладывает ограничения на значение R2. Чтобы величина параллельного соединения Rн и R2 не отличалась существенно от R2 достаточно выполнить условие неравенства
Rнмин ³10R2. (2.6)
Зная выходное сопротивление источника сигнала Rг и входное сопротивление Rн и задаваясь коэффициентом передачи делителя можно из (2.6) рассчитать сначала R 2, затем из (2.5) найти R 1. При расчете ДН также необходимо рассчитывать рассеиваемую мощность на резисторах и чувствительность схемы к разбросу параметров сопротивлений.
Рисунок 2.2 – Разновидности делителей напряжения
Важное место в электронике занимают делители напряжения, у которых верхнее или нижнее плечо образовано переменным сопротивлением. Если делитель запитать постоянным стабильным напряжением, и, скажем, в нижнем плече поставить сопротивление, величина которого завит от температуры, давления, влажности и пр. физических параметров (рис.2.3, а), то с выхода ДН можно снимать напряжение, пропорциональное температуре, давлению, влажности и т.д. Особое место занимают делители, у которых одно из сопротивлений зависит от частоты питающего напряжения. Они образуют большую группу разнообразных фильтров электрических сигналов.
Рисунок 2.3 – Делитель напряжение с переменным сопротивлением
Дальнейшее усовершенствование делителя напряжения привело к появлению измерительного моста, который состоит из двух делителей (рис. 2.3, б). В такой схеме можно снимать сигнал и между средней точкой и общим проводом, и между двумя средними точками. Во втором случае размах выходного сигнала при одинаковом изменении переменных сопротивлений удваивается. Усилители электрических сигналов также представляют собой делитель напряжения, роль переменного сопротивления в котором играет управляемый входным напряжением транзистор.
Интегрирующие линейные цепи
Простейшая интегрирующая цепочка представляет собой делитель напряжения, у которого роль нижнего плеча делителя выполняет конденсатор С (рис. 2.4).
Рисунок 2.4 – Интегрирующая линейная цепь
Замена нижнего сопротивления конденсатором радикально изменила частотные свойства делителя. Поскольку сопротивление конденсатора переменному току равно ZC = 1/wC, выражения (2.1) и (2.2) примут вид:
Анализ выражения (2.7) показывает, что при w = 0, ZC=¥, коэффициент передачи КДН =1,выходное напряжение Uвых будет равно Uвх, но по мере роста частоты входного сигнала КДН начинает снижаться. На АЧХ (рис.2.4, б) это снижение составляет 20 dB/дек. При частоте w = ¥, ZC становится равным нулю, т.е. конденсатор полностью шунтирует выходной сигнал, Uвых= 0. Эта особенность интегрирующих цепей получила широкое применение в электронных устройствах. Такая цепочка получила название фильтра нижних частот (ФНЧ). ФНЧ предназначен для передачи без изменения сигналов нижних частот, а на высоких частотах обеспечивает затухание сигналов и запаздывание их по фазе относительно входных сигналов. Такие свойства обеспечивает простейшая RС -цепь, изображенная на рис.2.4, а. Амплитудно-частотная характеристика такой цепи описывается уравнением:
а фазо-частотная φ (w) = − arctg wRC. (2.9) АЧХ и ФЧХ наиболее удобно представлять в логарифмическом масштабе. АЧХ для различных вариантов постоянных времени τ представлены на рис. 2.4, б. Граничная частота (частота среза) fср – это такая частота, при которой
Фазовый сдвиг φ на этой частоте составляет − 45°. Из выражения (2.11) вытекает, что чем меньше R и C, тем выше fср и тем шире полоса пропускания такой цепочки. Из рис. (2.4, б) видно, что АЧХ К (w) наиболее просто составить из двух асимптот: 1. К (w)= 1, что соответствует отсутствию затухания на нижних частотах f << fср, (K (w)= 0дБ) 2. На высоких частотах при f>>fср, (K (w) »1 /(wRC)) т. е. коэффициент усиления обратно пропорционален частоте, и при увеличении частоты в 10-раз K(w) также уменьшается в 10 раз, т. е. он уменьшается на 20 дБ на декаду. 3. K(w) = 1/ Цепь такой конфигурации (рис. 2.4, а) в электронной технике также называется интегрирующей, поскольку при соблюдении определенных соотношений между длительностью входного сигнала и параметром τ цепи позволяет получить на выходе интеграл от входного напряжения. Действительно, при R = 0 такая RС-цепь представляет собой идеальный интегратор тока:
Однако, поскольку в импульсной технике требуется интегрирование импульсов напряжения длительностью tи, можно искусственно создать источник тока с внутренним сопротивлением R. В этом случае уравнение (2.12) запишется в виде:
где первая составляющая определяет результат точного интегрирования, а вторая − погрешность интегрирования Duвых(t). В операторной форме уравнение (2.13) имеет вид
откуда видно, что рассматриваемая схема представляет собой инерционное звено первого порядка.
Если выполняется условие uвх (t) >>uвых (t), то интегралом от uвых (t) можно пренебречь и получить соотношения, описывающие идеализированный интегратор напряжения. Иначе говоря, фильтр нижних частот действительно можно считать интегрирующей цепью, выходное напряжение которой пропорционально интегралу входного напряжения. Функции интегрирующих цепей в устройствах импульсной техники могут быть различны. Такая цепочка может быть использована как фильтр нижних частот, сглаживающий фильтр постоянной составляющей (питающего напряжения), формирователь линейно изменяющегося напряжения, для расширения входных импульсов, для подавления коротких импульсных помех, паразитных обратных связей. Часто при анализе электронных схем приходится учитывать интегрирующие цепочки, образованные паразитными емкостями и сопротивлениями, которые могут существенно искажать форму импульсов. Случай передачи прямоугольного импульса напряжения наиболее часто встречается в схемах импульсной и цифровой техники. Рассмотрим физические процессы при воздействии на электрическую цепочку напряжением типа прямоугольного импульса. При нулевых начальных условиях (конденсатор разряжен) скачек напряжения на входе инициирует процесс заряда конденсатора по цепи: Ег – Rг – R – C – «земля» −Ег. Напряжение на конденсаторе (оно же – U вых) начнет нарастать по экспоненте. Как известно, начальный участок экспоненты близок к прямой. Если пренебречь внутренним сопротивлением источника сигнала, скорость нарастания UC определяется постоянной времени τзаряда = RC. Через время t ³ 5τ выходное напряжение практически станет равным Uвх. Это означает, что конденсатор полностью заряжен. По окончании импульса начинается процесс разряда конденсатора по цепи: верхняя обкладка конденсатора С – R – Rг − Ег – «земля» − нижняя обкладка С (окончание импульса нельзя рассматривать как «разрыв» в цепи источника сигнала). Таким образом, цепь разряда и цепь разряда – одна и та же. Следовательно, и постоянная времени разряда τразряда = τзаряда. Выходное напряжение Uвых спадает по такой же экспоненте, как и нарастало. Изменение выходного сигнала для этого случая при амплитуде входного импульса U maxв течении длительности импульса tи происходит по экспоненциальному закону
Переходные процессы для различных значений τ показаны на рис. 2.4, в. Очевидно, если соблюдается условие tи>>τ, то RС-цепь передает импульс практически без искажений. Чем ближе значения tи и τ, тем большие искажения претерпевает импульс. Если tи<<τ, то RС-цепь работает как интегрирующая с тем большей точностью интегрирования, чем лучше соблюдается это условие.
Можно заметить, что прямоугольный импульс, проходя через подобную RC-цепь, не только преобразуется по форме, но и растягивается по длительности.
|
||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 257; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.28.56 (0.008 с.) |

 , (2.1)
, (2.1)  , (2.2)
, (2.2) . (2.3)
. (2.3)
 . (2.5)
. (2.5) . (2.7)
. (2.7) , (2.8)
, (2.8)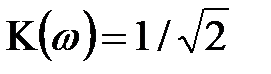 , т.e. изменяется на 3 дБ. Выражение для частоты среза fср получим, положив
, т.e. изменяется на 3 дБ. Выражение для частоты среза fср получим, положив , (2.10)
, (2.10)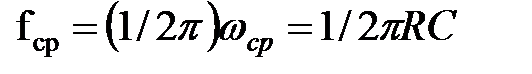 . (2.11)
. (2.11) , что соответствует затуханию на 3 дБ при f = fср.
, что соответствует затуханию на 3 дБ при f = fср. . (2.12)
. (2.12)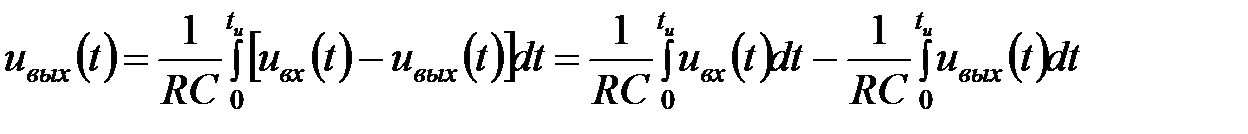 (2.13)
(2.13) , (2.14)
, (2.14) (2.15)
(2.15)


