
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Электронные элементы автоматикиСодержание книги
Поиск на нашем сайте
Учебное пособие
Утверждено редакционно-издательским советом университета, протокол № от
Харьков НТУ «ХПИ»
УДК ББК Г
Рецензенты:
Г.Ф. Кривуля, доктор техн. наук, профессор ХНУРЕ В.А. Маляренко, доктор. техн. наук, заслуженный деятель науки и техники Украины, профессор ХНУМГ им. О.М. Бекетова
У книзі розглядаються основи створення з напівпровідникових елементів (діоди, біполярні і польові транзистори, тиристори) різних функціональних вузлів аналогової техніки (підсилювачі, ключі, тригери). Викладено принципи з схематичної реалізації та дані методи розрахунку. Аналізуються статистичні, частотні та імпульсні характеристики пристроїв, наводяться еквівалентні схеми. Призначено для студентів технічних ВНЗ, а також може бути корисним для викладачів ВНЗ та інженерно-технічних працівників.
Іл. 121. Бібліогр. 27 найм.
Гапон А.И. Г Электронные элементы автоматики:учеб. пособие / А.И. Гапон, И.Г. Либерг, В.А. Крылова – Х.: НТУ «ХПИ», 2015. – 232с. – На русском языке
ISBN
В книге рассматриваются основы создания из полупроводниковых элементов (диоды, биполярные и полевые транзисторы, тиристоры) различных функциональных узлов аналоговой техники (усилители, ключи, триггеры). Изложены принципы их схемотехнической реализации и даны методы расчета. Анализируются статистические, частотные и импульсные характеристики устройств, приводятся эквивалентные схемы. Предназначено для студентов технических вузов, а также может быть полезным для преподавателей вузов и инженерно-технических работников.
Ил. 121. Библиогр. 27 назв.
УДК ББК
ISBN © А.И. Гапон, И.Г. Либерг, В.А. Крылова, 2015 СПИСОК ОСНОВНЫХ СОКРАЩЕНИЙ
Введение
Одним из главных факторов, обеспечивающих развитие всех отраслей производства, является комплексная автоматизация производственных процессов на основе последних достижений электронной техники. Особенно возрасла роль электроники с развитием микросхемотехники, которая позволяет существенно уменьшить габаритные размеры, массу, автоматизировать процесс изготовления электронных устройств, значительно повысить надежность электронных систем автоматики и упрвления. К электронным устройствам автоматики предъявляются высокие требования, так как современная электронная аппаратура должна обеспечивать надежность работы сложнейших систем автоматического управления и контроля. Современный этап развития радиоэлектронной аппаратуры характеризуется все более широким применением интегральных схем высокой функциональной сложности. Это требует нового подхода к написанию современных учебников и учебных пособий радиоэлектронного направления. Роль электронных устройств автоматики и управления особенно возрастает в настоящее время в связи с широким применением микропроцессорной техники для переработки информационных сигналов. Область использования интегральных микросхем непрерывно расширяется, они выполняют все более сложные функции включают в себя большее число отдельных электронных элементов. Независимо от степени сложности микросхем выполняемых ими функций основу их структуру составляют элементарные схемы, физические принципы и особенности, работы которых наиболее просто и эффективно проявляются при моделировании микросхем с помощью отдельных дискретных электронных и электрических элементов. В учебнике изложены принципы построения и характеристики современных элементов и устройств электронных систем автоматики и управления, предназначенных для формирования, генериррвания и обработки информационных сигналов. Особое внимание уделено дискретным и цифровым устройствам, а также устройствам преобразования аналоговых и цифровых сигналов. Рассматриваются внешние характеристики различных электронных схем и описывающие их математические и схемные модели, приведен анализ работа как системы, состоящей из более простых элементов. Многочисленные примеры схемотехнической реализации устройств автоматического управления, анализ их работы и необходимые расчетные формулы, описания физических процессов, составляющих сущность функционирования устройств, развернутый справочный материал, а также избранный стиль изложения материала – популярный, должны сделать книгу интересной и доступной для широкого круга читателей. Книга адресована как студентам, специализирующихся в области физики, информатики и инженерных наук, так и практическим работникам, которые желают пополнить свои знания в области физики электронных цифровых элементах автоматики и микроэлектроники. В пределах ограниченных объемом одной книги, невозможно отразить схемотехнику всех существующих элементов электроники и автоматики. Эту задачу могли бы решить только соответствующее многотомное издание. Поэтому в этой книге с позиции теории и анализа раскрыты основы и общие приёмы проектирования базовых электронных элементов автоматики: простейшие электрические цепи, усилители, генераторы и формирователи электрических сигнавлов, выполненные на дискретных элементах, простейших интегральных схемах, интегральных схемах более высокой степени сложности. При этом основное внимание уделяется принципам построения и особенностям работы типовых электронных устройств, из которых можно составлять схемы практической сложности. Электрические сигналы 1.1. Термины и определения Сигнал − это физический носитель сообщения о каких-либо событиях, состояниях объекта, командах управления и т. п. Сигнал имеет две стороны: содержание и форму. Содержание определяется сообщением (информацией). Форма сигнала определяется характером изменения его параметров, в соответствии с информацией, которая подлежит передаче или хранению. Выбор той или иной формы представления информации называется кодированием и зависит от способа ее дальнейшей обработки. Обратная операция − выявление закодированной в сигнале информации − называется декодированием. Наряду с сигналами в исследованиях электронных устройств широко применяют воздействия −сигналы специального вида. Их подбирают так, чтобы нужные характеристики устройств получались наиболее просто (чаще всего это воздействия вида единичного скачка, либо дельта-функция). В рассматриваемых электронных цепях носителями информации являются электрические колебания. Процесс изменения параметров электрических колебаний принято называть модуляцией. Модуляцияможет быть выполнена различными способами. Если сообщение передается за счет непрерывного изменения параметра электрических колебаний, то говорят о непрерывной, или аналоговой, модуляции. При этом переносчиком информации (информативным параметром колебаний) могут быть амплитуда, частота, фаза или их комбинация.На рис. 1.1 приведены наиболее употребительные в автоматике сигналы для передачи непрерывных величин. Это могут быть напряжение или ток с медленноменяющимся уровнем и изменяющимся направлением (рис 1.1, а),либо гармонические колебания с изменяющейся амплитудой (AM) (рис 1.1,б), частотой (ЧМ) или фазой (ФМ), (рис 1.1, в), или с тем и другим одновременно (АФМ) (рис 1.1, г). Амплитудно-фазовая модуляция характерна для устройств автоматики, где значение входного воздействия определяет амплитуду гармонических колебаний, а изменение знака этого воздействия на противоположный меняет на 180° фазу колебаний. Синусоидальные колебания высокой, так называемой несущей, частоты играют роль переносчика информации. Передаваемый низкочастотный сигнал заложен в изменениях какого-либо параметра колебаний несущей частоты. Обратное преобразование − отделение сигнала от его переносчика называют демодуляцией или детектированием
Рисунок 1.1 − Сигналы для передачи непрерывных величин:
В качестве переносчика сигнала можно использовать не только постоянный (медленно-меняющийся) или синусоидальный ток. Поскольку В.А. Котельниковым [1] было показано, что для большинства непрерывных функций достаточно передать определенный ряд их мгновенных значений, чтобы на приемном конце системы связи можно было восстановить первоначальную функцию х(t) с наперед заданной точностью, для передачи сообщения можно также использовать периодические последовательности импульсов, обычно прямоугольной формы (рис. 1.2). Применяют амплитудно-импульсную модуляцию (АИМ) (рис.1.2, в), частотно-импульсную модуляцию (ЧИМ) (рис. 1.2, е), фазо-импульсную модуляцию (ФИМ) (рис. 1.2, г), широтно-импульсную модуляцию (ШИМ) (рис. 1.2, д). Здесь исходная информация передается за счет модуляции длительности импульсов tи при постоянной частоте следования импульсов.
Рисунок 1.2 − Периодическая последовательность прямоугольных импульсов
Как правило, модуляция-демодуляция используется там, где необходимо через один физический канал передавать одновременно несколько сообщений, т.е. осуществить «уплотнение канала». Таким образом, например, можно по одной паре проводов передать телефонный разговор нескольких пар абонентов, или информацию в систему управления от нескольких датчиков. При выборе типа модуляции необходимо учитывать как достоинства, так и недостатки, присущие каждому типу. Так амплитудная модуляция (АМ), которая широко используется, например, для вещательных станций в диапазонах длинных, средних и коротких волн, а также в трехпрограммной ретрансляционной радиосети отличается простотой реализации устройств и передатчика и приемника (генератора несущей частоты, модулятора, демодулятора, усилителя). Сигналы, прошедшие процедуру амплитудной модуляции можно смешивать и передавать в один общий канал связи, а в приемнике выделить из пришедшей смеси свой сигнал с помощью частотного фильтра, и затем демодулировать его. Но такой способ передачи информации отличается низкой помехоустойчивостью. На полезный сигнал легко накладываются помехи от атмосферных электрических разрядов, промышленных электрических сетей. Кроме того, качество приема сильно зависит от свойств проводящей среды (атмосферы или проводной линии), которые изменяют амплитуду принимаемого сигнала, и могут иметь сильные колебания, например, суточной или годовой периодичности. Частотная модуляция по помехоустойчивости значительно превосходит АМ, поскольку частоту принимаемого сигнала невозможно изменить колебаниями электрических и магнитных свойств проводящей среды. Но требования к точности работы передающей и приемной аппаратуры гораздо выше, что влечет повышение сложности и удорожание аппаратуры. ЧМ используется в УКВ (ФМ) диапазоне радиовещания и в телевидении. Фазовая модуляция позволяет еще больше уплотнить канал, поскольку несущие частоты передатчиков требуется разносить на значительно меньшую величину. Однако ФМ требует еще большей точности и стабильности аппаратуры. Кроме того ФМ уже «чувствует» скорость взаимного перемещения приемника и передатчика (эффект Доплера). Импульсная модуляция обладает рядом преимуществ, важнейшее из которых – экономичность. Если в аналоговой модуляции усилительные элементы практически все время работают в активном режиме, рассеивая в виде тепла до 50% энергии источника питания, то в режиме импульсной модуляции транзисторы работают в режиме ключа. Особенность этого режима заключается в том, что усилительный элемент (транзистор) большую часть времени находится либо в режиме отсечки, когда ток через него практически равен нулю, либо в режиме насыщения, когда напряжение на открытом транзисторе составляет десятые доли вольт. И в том и в другом случае доля мощности, рассеиваемая на транзисторных ключах не превышает 10% от мощности, потребляемой устройством от источника питания. Переход к импульсным системам позволяет простыми аппаратными средствами достичь уплотнения канала за счет введения, так называемого релейного режима связи. Для этого все N непрерывных сигналов подвергаются, например, амплитудно-импульсной модуляции. Затем в канал циклически посылается по одному импульсу от 1, 2, …, N источника сигнала последовательно. В канале образуется смесь импульсов, «принадлежащих» разным источникам. Чтобы восстановить на приемной стороне исходную информацию необходимо выбирать из канала «свои» импульсы в такой же последовательности, в какой они посылались (что требует соответствующей синхронизации работы всей системы), и подвергнуть их демодуляции. Особо необходимо отметить, что нарушение порядка выборки «своих» импульсов приводит к полному хаосу на принимающей стороне. Эта особенность может использоваться для «засекречивания» информации. Система частотно-импульсной модуляции обладает значительно большей помехоустойчивостью, но не допускает вышеописанного способа уплотнения канала. Фазо-импульсная модуляция лишена недостатков АИМ и ЧИМ, но требует очень точной синхронизации и высокой стабильности работы передающей и принимающей аппаратуры. Широтно-импульсная модуляция не имеет прототипа в аналоговой модуляции. Благодаря простоте реализации и высокой помехоустойчивости ШИМ получила широкое распространение в устройствах автоматики. Заметим, что в ряде систем автоматики передаваемые импульсы могут иметь высокочастотное заполнение. Сначала непрерывный сигнал подвергается, например, широтно-импульсной модуляции, а затем полученным видеоимпульсом модулируют высокочастотный гармонический сигнал, т.е. используется комбинация импульсной и аналоговой модуляции. Сообщение может быть также передано в виде кода, т.е. составленных по определенным правилам комбинаций дискретных сигналов (импульсов). В этом случае передаваемая информация не зависит от частоты, амплитуды и длительности импульсов. Наконец, сообщение может быть передано в цифровой форме, когда оно описывается упорядоченной совокупностью цифр с конечным (заранее выбранным) числом разрядов. В свою очередь, каждая цифра может быть закодирована определенной комбинацией импульсов. При кодировании передаваемая информация не зависит от частоты, амплитуды и длительности импульсов. Процесс кодирования неразрывно связан с преобразованием непрерывных величин в дискретные. Такое преобразование основывается на операциях дискретизации (квантования по времени), квантования по уровню и совокупности этих операций − комбинированному квантованию. Дискретизация, или квантование по времени, представляет собой преобразование непрерывного сигнала х (t)(рис. 1.3 ) в последовательность мгновенных значений этого сигнала хд (kT),соответствующих определенным, обычно равноотстоящим, или переменным отрезкам времени Т. Промежуток времени между двумя соседними моментами дискретизации называется шагом дискретизации или шагом квантования по времени.
Рисунок 1.3 – Дискретизация по времени
Шаг квантования Т выбирается таким образом, чтобы дискретная функция по возможности точно отражала непрерывную функцию. Иначе говоря, чтобы при квантовании как можно меньше терялась информация, содержащаяся в непрерывной функции. Согласно теореме Котельникова, функция времени х (t), не содержащая составляющих частоты выше f Гц, полностью определяется своими значениями в моменты времени, отстоящими друг от друга на 1/2 f секунд. И если полезный сигнал х (t)не содержит частот выше f, то, после квантования с шагом Т = 1/2 f, можно быть уверенным, что дискретная функция точно отобразит непрерывную функцию, т. е. потери информации при квантовании не произойдет, т. е.
где k =1, 2, …, n.
Квантование по уровню − это преобразование непрерывно изменяющейся величины в ступенчато изменяющуюся с заданными постоянными или переменными размерами ступеней (рис. 1.4). Ступенью квантования, или шагом квантования по уровню DХ, называется разность между двумя соседними заданными значениями квантованной величины.
Рисунок 1.4 – Квантование по уровню
Число разрешенных уровней квантования т определяется максимальным уровнем сигнала Х maх и шагом квантования по уровню DХ по формуле:
т = Х maх / DХ. (1.2)
При комбинированном квантовании непрерывный сигнал x (t)квантуется по времени и по уровню, т.е. функция непрерывного сигнала заменяется дискретными значениями в моменты времени, отстоящими друг от друга на шаг квантования по времени Т, их амплитуды определяются ближайшими уровнями квантования. Восстановление квантованного сигнала получается с погрешностью, которая определяется разностью между значениями квантованных дискретных импульсов и функцией непрерывного сигнала в точках отсчета. Погрешность квантования, или шум квантования, принято приближенно оценивать мощностью шума квантования σ 2= DU 2/12. Дискретное кодирование непосредственно используется в дельта-модуляции (ДМ) и импульсно-кодовой модуляции (ИКМ). При ДМ непрерывный исходный сигнал x (t)аппроксимируется следящим ступенчатым сигналом G (t) (рис. 1.5). Степень соответствия функций x (t)и G (t) определяется значениями шагов квантования по времени Т и по уровню DХ. В соответствии с функцией ступенчатого сигнала G (t) в моменты ее скачкообразного изменения получают модулированный сигнал х дм в виде одиночных импульсов (постоянной длительности и амплитуды) положительной или отрицательной полярности в соответствии с направлением изменения функции G (t ). Импульсы отражают знак разности между текущей выборкой и ее прогнозированным значением, в качестве которого берется квантованное значение предшествующей выборки. Таким образом, при ДМ значение сообщения в каждой точке кодируется одноразрядным двоичным кодом. При ИКМ непрерывный сигнал х (t)предварительно квантуется по времени и по уровню, а затем каждому дискретному значению уровня сигнала присваивается соответствующая кодовая комбинация. Таким образом, исходное сообщение передается кодовыми комбинациями, соответствующими дискретным значениям, которые отражают непрерывный сигнал х (t). Количество единичных элементов кодовой комбинации п определяется основанием кода и количеством уровней квантования T. Так как, для ИКМ обычно используется двоичный код, то
п = log2m. (1.3)
Величина шага квантования по времени Т выбирается в соответствии с теоремой Котельникова, а количество уровней квантования т− необходимой степенью точности воспроизведения сигнала с учетом того, что значение п должно быть целым числом. Примером является ИКМ с использованием трехразрядного двоичного кода п = 3, где наличие импульса соответствует числу 1, а отсутствие − 0. Модулируемый непрерывный сигнал х (t)разбит на 2 n = 23 = 8 уровней. Каждому уровню соответствует свой двоичный код. На временной оси этот код отражается комбинацией из трех импульсов, каждый из которых в соответствии с занимаемой позицией на одном отрезке квантования Т имеет свой «вес»: 2°, 21 или 22. Наличие на данном шаге квантования импульсов с тем или иным весом определяет уровень квантования. Например, при наличии всех трех импульсов (двоичный код 111) уровень квантования равен 7.
Рисунок 1.5 – Дельта-модуляция
Выбирая метод дискретизации, необходимо учитывать особенности последующей передачи информации. Так, при дискретизации по времени канал связи легко мультиплексировать. Но канал будет периодически задействоваться, даже если никакой новой информации о состоянии объекта передаваться и не будет. Например, если измерять температуру объекта, которая в силу неизменности внешних условий на длительное время застабилизировалась, то многократные сообщения о температуре объекта ничего нового содержать не будут. С другой стороны, при квантовании по уровню достигается высокая экономичность устройства, хотя канал мультиплексировать намного труднее, и длительное «молчание» в этом случае можно спутать с отказом датчика или передающей аппаратуры. К характеристикам, с помощью которых обычно описываются электрические сигналы, относят динамический диапазон, время установления и ширина спектра сигнала. Динамическим диапазоном называют отношение наибольшей мгновенной (так называемой пиковой) мощности сигнала к его наименьшей (пороговой) мощности. Помимо сигналов, несущих нужную информацию, из окружающего пространства поступают посторонние электромагнитные сигналы, так называемые шумы и помехи, которые подавляют, маскируют полезный сигнал. Для удовлетворительного приема сообщений необходимо иметь возможность различать полезный сигнал на фоне помех и шумов, что диктует ограничения по наименьшей (пороговой) мощности полезного сигнала. Говорят о необходимом отношении сигнал-помеха, точнее − отношении средних мощностей сигнала и помехи. Необходимо повышать его за счет повышения энергии передаваемого сигнала и снижения уровня помехи, хотя чрезмерное увеличение мощности сигнала может привести к искажению его формы, а следовательно, и содержащейся в нем информации из-за ограниченной выходной мощности систем передачи. Появление таких искажений ставит предел наибольшей (пиковой) мощности сигнала. Оценка по времени установления, т. е. времени, в течение которого сигнал (с заданной точностью) достигает установившегося значения, необходима для суждения об искажениях, которые могут возникнуть из-за инерционности реальных датчиков, устройств передачи и приема сигналов. Подобные оценки получают двояким способом: заданием либо функции времени (временной характеристики), описывающей реальный процесс, либо ряда гармонических колебаний, т, е. спектра, который есть функция частоты. Оба представления равносильны и взаимно дополняют друг друга, а переход от одного к другому осуществляется с помощью прямого и обратного преобразований Фурье и Лапласа. Например, назначение всякого фильтра состоит в том, чтобы пропустить колебания одних частот и задержать колебания других частот. Поэтому свойства фильтра принято описывать с помощью спектральных представлений. Если разработчика интересуют искажения формы импульсов в цифровых схемах преобразования или передачи импульсов, то их удобно представить функциями времени. Таким образом, выбор способа описания системы зависит не столько от ее устройства, сколько от ее назначения.
Спектр сигнала
Предположим, что сигнал представляет собой воздействие в виде периодической функции времени х (t)с периодом Т = 1/ f, которую можно представить рядом Фурье:
где w = 2 pf 0; j 1, j 2, j 3 … − начальные фазы отдельных гармоник; Х1m, Х2m, Х3т,... − амплитуды отдельных гармоник:
Коэффициенты Фурье
Смысл формулы (1.4) состоит в том, что любая периодическая функция х (t)может быть представлена суммой синусоидальных колебаний с частотами, кратными основной частоте w, и с соответствующими амплитудами и начальными фазами. Отдельные слагаемые суммы (1.4) называются гармониками. Колебания основной частоты w 1 называют первой гармоникой, колебание с частотой w 2 − второй гармоникой и т. д. Постоянная составляющая
представляет собой среднее значение функции х (t). Совокупность величин Xkm называется спектром амплитуд; совокупность величин jk − спектром фаз. Чаще всего интересуются только спектром амплитуд и называют его для краткости просто спектром. Графически спектр изображают в координатах Cm, w (рис. 1.6). Длины вертикальных отрезков представляют собой амплитуды соответствующих гармоник; эти отрезки называют спектральными линиями, а сам спектр − линейчатым. В общем случае сумма (1.4) является бесконечным рядом. Но в действительности для всех сигналов число членов ряда, а следовательно, и число спектральных линий конечно, так как амплитуды гармоник, начиная с некоторого номера, становятся настолько малы, что ими можно пренебречь, не нарушая смысла сообщения. Таким образом, сигналы в системе управления и связи практически всегда представляются функциями с ограниченным спектром. Интервал частот, в котором размещается ограниченный спектр, называется шириной спектра. Ограничение спектра производят, исходя из допустимого искажения сигнала, так, чтобы не потерять содержащуюся в нем информацию.
Рисунок 1.6 – Спектр сигнала
В качестве примера рассмотрим амплитудно- модулированный сигнал
в котором х (t)описывается выражением (1.4). Обычно частота w нес на один - два порядка превышает высшую гармонику nw 1 сигнала x (t), поэтому говорят, что амплитуда несущих колебаний медленно меняется в соответствии с сигналом, а высокочастотные колебания являются переносчиком информации. Например, сигнал медленноменяющегося постоянного тока x (t)не может пройти через емкостную цепь, но легко может быть передан в нагрузку посредством амплитудной модуляции с последующей демодуляцией его. Как видно из (1.9), амплитудная модуляция осуществляется в результате нелинейногопреобразования сигнала − умножения гармонического колебания с постоянной амплитудой U 0 и сигнала х (t). В результате получается негармоническое колебание, имеющее сложный спектр. Чтобы представить его, упростим задачу, положив x (t)= cos Ω t. После подстановки х (t)в выражение (1.9) и перемножения функций получим
Иначе говоря, AM-колебание содержит три составляющие: колебание несущей частоты При частотной модуляции (ЧМ) амплитуда несущих колебаний постоянна, а приращение, пропорциональное х (t), получает частота несущих колебаний wнес = w0 + Dw x (t); при фазовой модуляции фаза колебаний φ = φ0 + Dφ x (t). (Здесь Dw и Dφ − частотное и фазовое отклонения, которые определяют глубину модуляции и выбираются по усмотрению проектировщика). Форма напряжения сигнала несущей с ЧМ приведена ранее, на рис. 1.2. Аналогичным будет и сигнал с ФМ. Модулирующая функция х (t)изменяется по треугольному закону (рис. 1.2). ФМ можно рассматривать как разновидность ЧМ и наоборот. Ширина спектра ЧМ-колебаний может быть определена как 2 Dw и называется также полосой качания,так как в процессе модуляции частота может принимать любое мгновенное значение в интервале w0 ± Dw. При AM ширина спектра не зависит от интенсивности модулирующего сигнала, а при ЧМ - прямо пропорциональна амплитуде модулирующих колебаний.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 134; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.88.18 (0.011 с.) |

 (1.1)
(1.1) , (1.4)
, (1.4) . (1.5)
. (1.5) ; (1.6)
; (1.6) . (1.7)
. (1.7)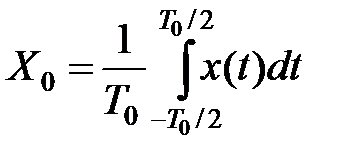 (1.8)
(1.8)

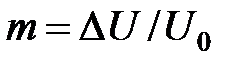 , (1.9)
, (1.9) . (1.10)
. (1.10)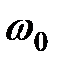 и два колебания с частотами
и два колебания с частотами  ± Ω, которые называются боковыми частотами. Спектр АМ-колебаний состоит из трех линий (рис. 1.6). В общем случае при AM ширина спектра равна удвоенной ширине спектра модулирующей функции (точнее, удвоенной высшей частоте этого спектра). Амплитуда боковых частот пропорциональна
± Ω, которые называются боковыми частотами. Спектр АМ-колебаний состоит из трех линий (рис. 1.6). В общем случае при AM ширина спектра равна удвоенной ширине спектра модулирующей функции (точнее, удвоенной высшей частоте этого спектра). Амплитуда боковых частот пропорциональна  , т. е. глубине модуляции; при отсутствии модуляции боковых частот нет, а при наиболее глубокой модуляции амплитуды боковых частот равны половине амплитуды несущей.
, т. е. глубине модуляции; при отсутствии модуляции боковых частот нет, а при наиболее глубокой модуляции амплитуды боковых частот равны половине амплитуды несущей.


