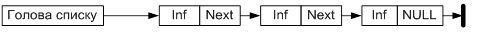Однонаправлений лінійний список.

Зв’язний список (linked list) — це структура даних, у якій об’єкти розташовані у лінійному порядку. Однак, на відміну від масиву, у якому цей порядок визначається індексами, порядок у зв’язному списку визначається вказівниками (покажчиками) на кожен об’єкт.

На рисунку, поданому нижче, наведено структуру однозв’язного списку. Кожний список повинен мати особливий елемент, який називається покажчиком на початок списку, або головою списку.

Двонаправлений лінійний список.

Проте, оброблення однозв’язного списку не завжди є зручним, оскільки відсутня можливість просування в протилежну сторону. Таку можливість забезпечує двох-зв’язний список, кожний елемент якого містить два покажчики: на наступний і попередній елементи списку.

Основні поняття мультисписків.

Для того, щоб при вибірці кожної підмножини не виконувати повний перегляд з відсіванням записів, які до необхідної підмножини не відносяться, в кожний запис включаються додаткові поля посилань, кожне з яких зв’язує в лінійний список елементи відповідної підмножини. В результаті виходить багато-зв’язковий список або мультисписок, кожний елемент якого може входити одночасно в декілька однозв’язних списків.

 

Стрічка як структура даних.

Стрічка – це лінійно впорядкована послідовність символів, які належать до скінченої множини символів, яка називається алфавітом.

Стрічки мають наступні важливі властивості:

· їхня довжина, як правило, змінна, хоч алфавіт фіксований;

· звичайне звернення до символів стрічки йде з будь-якого одного боку послідовності (важлива впорядкованість послідовності, а не її індексація);

· метою доступу до стрічки є на окремий її елемент, а ланцюжок символів.

Базовими операціями над стрічками є:

· визначення довжини стрічки;

· присвоєння стрічки;

· конкатенація (зчеплення) стрічок;

· виділення підстрічки;

· пошук входження.

Зв’язне представлення даних.

Оскільки елементи динамічної структури розташовуються за не передбачуваними адресами пам’яті, адресу елемента такої структури не можна обчислити за адресою початкового або попереднього елемента. Для встановлення зв’язку між елементами динамічної структури використовуються покажчики, через які встановлюються явні зв’язки між елементами. Таке представлення даних в пам’яті називається зв’язним. Елемент динамічної структури складається з двох полів:

· інформаційного поля або поля даних, в якому містяться ті дані, заради яких і створюється структура;

· поле зв’язку, в якому міститься один або декілька покажчиків, які зв’язують даний елемент з іншими елементами структури.

Коли зв’язне представлення даних використовується для вирішення прикладної задачі, для кінцевого користувача „видимим” робиться тільки вміст інформаційного поля, а поле зв’язку використовується тільки програмістом-розробником.

Переваги зв’язного представлення даних:

· можливість забезпечення значної змінності структур;

· розмір структури обмежується тільки доступним об’ємом машинної пам’яті;

· при зміні логічної послідовності елементів структури потрібно виконати не переміщення даних в пам’яті, а тільки корекцію покажчиків.

Разом з тим зв’язне представлення не позбавлене й недоліків, основні з яких:

· робота з покажчиками вимагає більш високої кваліфікації від програміста;

· на поля зв’язку витрачається додаткова пам’ять;

доступ до елементів зв’язної структури може бути менш ефективним за часом.

Представлення графа як структури даних.

Граф – це складна нелінійна багато-зв’язна динамічна структура, що відображає властивості і зв’язки складного об’єкту.

Ця багато-зв’язна структура має наступні властивості:

· на кожний елемент (вузол, вершину) може бути довільна кількість посилань;

· кожний елемент може мати зв’язок з будь-якою кількістю інших елементів;

· кожний зв’язок (ребро, дуга) може мати напрям і вагу.

Існує два основні методи представлення графів в пам’яті комп’ютера: матричний і зв’язними нелінійними списками.

Дерево як структура даних.

Дерево – це граф, який характеризується наступними властивостями:

· Існує єдиний елемент (вузол або вершина), на який не посилається ніякий інший елемент, – він називається коренем.

· Починаючи з кореня і слідуючи по певному ланцюжку покажчиків, що містяться в елементах, можна здійснити доступ до будь-якого елемента структури.

· На кожний елемент, крім кореня, є єдине посилання, тобто кожний елемент адресується єдиним покажчиком.

29. Алгоритм перетворення дерева в бінарне.

Правило побудови бінарного дерева з будь-якого дерева:

1. В кожному вузлі залишити тільки гілку до старшого сина;

2. З’єднати горизонтальними ребрами всіх братів одного батька;

3. Таким чином перебудувати дерево за правилом:

лівий син – вершина, розташована під даною;

правий син – вершина, розташована праворуч від даної (тобто на одному ярусі з нею).

4. Розвернути дерево так, щоб усі вертикальні гілки відображали лівих синів, а горизонтальні – правих.

У результаті перетворення будь-якого дерева, в бінарне, виходить дерево у вигляді лівого піддерева, підвішеного до кореня.

30. Представлення дерев у пам’яті.

Представити m -арне дерево в пам’яті комп’ютера складно, так як кожен елемент дерева повинен містити стільки покажчиків, скільки ребер, виходить з вузла. Це приведе до підвищеної витрати пам’яті, різноманітності початкових елементів і ускладнить алгоритми обробки дерева. Тому m -арні дерева, ліс необхідно привести до бінарних для економії пам’яті і спрощенню алгоритмів. Усі вузли бінарного дерева представляються в пам’яті однотипними елементами з двома покажчиками, крім того, операції над бінарними деревами виконуються просто і ефективно.

Дерева можна представляти за допомогою зв’язних списків і масивів (або послідовних списків).

Частіше всього використовується зв’язне представлення дерев, так як воно дуже сильно нагадує логічне. Зв’язне зберігання полягає в тому, що задається зв’язок від батька до синів. В бінарному дереві є два покажчики, тому зручно вузол представити у вигляді структури в якій left – покажчик на ліве піддерево, right – покажчик на праве піддерево, inf – містить інформацію, яка зв’язана з вершиною і має наперед визначений тип – data.

31. Операції над деревами.

Над деревами визначені наступні основні операції:

1) Пошук вузла із заданим ключем.

2) Додавання нового вузла.

3) Видалення вузла (піддерева).

4) Обхід дерева в певному порядку:

Низхідний обхід;

Змішаний обхід;

Висхідний обхід.

32. Алгоритми обходу дерева.

Схемно алгоритм обходу бінарного дерева відповідно до низхідного способу може виглядати таким чином:

1. В якості чергової вершини взяти корінь дерева. Перейти до пункту 2.

2. Провести обробку чергової вершини відповідно до вимог задачі. Перейти до пункту 3.

3.а) Якщо чергова вершина має обидві гілки, то в якості нової вершини вибрати ту вершину, на яку посилається ліва гілка, а вершину, на яку посилається права гілка, занести в стек; перейти до пункту 2;

3.б) якщо чергова вершина є кінцевою, то вибрати в якості нової чергової вершини вершину із стека, якщо він не порожній, і перейти до пункту 2; якщо ж стек порожній, то це означає, що обхід всього дерева закінчений, перейти до пункту 4;

3.в) якщо чергова вершина має тільки одну гілку, то в якості чергової вершини вибрати ту вершину, на яку ця гілка вказує, перейти до пункту 2.

4. Кінець алгоритму.

Алгоритм істотно спрощується при використовуванні рекурсії. Так, низхідний обхід можна описати таким чином:

1). Обробка кореневої вершини;

2). Низхідний обхід лівого піддерева;

3). Низхідний обхід правого піддерева.

Змішаний обхід можна описати таким чином:

1) Спуститися по лівій гілці із запам’ятовуванням вершин в стеку;

2) Якщо стек порожній те перейти до п.5;

3) Вибрати вершину із стеку і обробити дані вершини;

4) Якщо вершина має правого сина, то перейти до нього; перейти до п.1.

5) Кінець алгоритму.

Рекурсивний змішаний обхід описується таким чином:

1) Змішаний обхід лівого піддерева;

2) Обробка кореневої вершини;

3) Змішаний обхід правого піддерева.

Алгоритм висхідного обходу можна представити таким чином:

1) Спуститися по лівій гілці із запам’ятовуванням вершини в стеку як 1-й вид стекових записів;

2) Якщо стек порожній, то перейти до п.5;

3) Вибрати вершину із стека, якщо це перший вид стекових записів, то повернути його в стек як 2-й вид стекових записів; перейти до правого сина; перейти до п.1, інакше перейти до п.4;

4) Обробити дані вершини і перейти до п.2;

5) Кінець алгоритму.

Рекурсивний змішаний обхід описується таким чином:

1). Висхідний обхід лівого піддерева;

2). Висхідний обхід правого піддерева;

3). Обробка кореневої вершини.