
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Принципи формалізації алгоритмів.Содержание книги
Поиск на нашем сайте
Покрокове проектування алгоритмів. 35. Основні характеристики алгоритмів. 36. Поняття складності алгоритму. Ефективність алгоритмів. Правила аналізу складності алгоритмів. Постановка задачі сортування. 40. Класифікація алгоритмів сортування.
41. Сортування вибіркою. Сортування вибором — простий алгоритм сортування лінійного масиву, на основі вставок. Має ефективність n 2, що робить його неефективним при сортування великих масивів, і в цілому, менш ефективним за подібний алгоритм сортування включенням. Сортування вибором вирізняється більшою простотою, ніж сортування включенням, і в деяких випадках, вищою продуктивністю. Алгоритм працює таким чином:
42. Сортування включенням. Цей метод – „дослівна” реалізації стратегії включення. Порядок алгоритму сортування простим включенням – Сортування вставкою (включенням) — простий алгоритм сортування на основі порівнянь. Має цілу низку переваг:
Сортування розподілом. 44. Сортування злиттям. В основі цього способу сортування лежить злиття двох упорядкованих ділянок масиву в одну впорядковану ділянку іншого масиву. Злиття двох упорядкованих послідовностей можна порівняти з перебудовою двох колон солдатів, вишикуваних за зростом, в одну, де вони також розташовуються за зростом. Якщо цим процесом керує офіцер, то він порівнює зріст солдатів, перших у своїх колонах і вказує, якому з них треба ставати останнім у нову колону, а кому залишатися першим у своїй. Так він вчиняє, поки одна з колон не вичерпається — тоді решта іншої колони додається до нової. Принципи рандомізації. Постановка задачі пошуку. 47. Послідовний пошук. Найпростішим методом пошуку елемента, який знаходиться в неврегульованому наборі даних, за значенням його ключа є послідовний перегляд кожного елемента набору, який продовжується до тих пір, поки не буде знайдений потрібний елемент. Якщо переглянуто весь набір, і елемент не знайдений – значить, шуканий ключ відсутній в наборі. Цей метод ще називають методом повного перебору. 48. Бінарний пошук. Іншим, відносно простим, методом доступу до елемента є метод бінарного (дихотомічного) пошуку, який виконується в явно впорядкованій послідовності елементів. Оскільки шуканий елемент швидше за все знаходиться „десь в середині”, перевіряють саме середній елемент: a[N/2]==key? Якщо це так, то знайдено те, що потрібно. Якщо a[N/2]<key, то значення i=N/2 є замалим і шуканий елемент знаходиться „праворуч”, а якщо a[N/2]>key, то „ліворуч”, тобто на позиціях 0…i. Для того, щоб знайти потрібний запис в таблиці, у гіршому випадку потрібно log2(N) порівнянь. Це значно краще, ніж при послідовному пошуку. 49. Пошук методом інтерполяції. Якщо немає ніякої додаткової інформації про значення ключів, крім факту їхнього впорядкування, то можна припустити, що значення key збільшуються від a[0] до a[N-1] більш-менш „рівномірно”. Це означає, що значення середнього елементу a[N/2] буде близьким до середнього арифметичного між найбільшим та найменшим значенням. Але, якщо шукане значення key відрізняється від вказаного, то є деякий сенс для перевірки брати не середній елемент, а „середньо-пропорційний”. Вираз для поточного значення i одержано з пропорційності відрізків:
В середньому цей алгоритм має працювати швидше за бінарний пошук, але у найгіршому випадку буде працювати набагато довше. 50. Пошук методом „золотого перерізу”. Деякий ефект дає використання так званого „золотого перерізу”. Це число
Доданій корінь Згідно цього алгоритму відрізок слід ділити не навпіл, як у бінарному алгоритмі, а на відрізки, пропорційні 51. Алгоритми пошуку послідовностей. КМП-пошук дає справжній виграш тільки тоді, коли невдачі передувала деяка кількість збігів. Лише у цьому випадку слово зсовується більше ніж на одиницю. На жаль, це швидше виняток, ніж правило: збіги зустрічаються значно рідше, ніж незбіги. Тому виграш від практичного використання КМП-стратегії в більшості випадків пошуку в звичайних текстах досить незначний. Метод, який запропонували Р. Боуєр і Д. Мур в 1975 р., не тільки покращує обробку самого поганого випадку, але й дає виграш в проміжних ситуаціях. БМ-пошук базується на незвичних міркуваннях – порівняння символів починається з кінця слова, а не з початку. Як і у випадку КМП-пошуку, слово перед фактичним пошуком трансформується в деяку таблицю. Нехай для кожного символу x із алфавіту величина dx – відстань від самого правого в слові входження x до правого кінця слова. Уявимо, що виявлена розбіжність між словом і текстом. У цьому випадку слово відразу ж можна зсунути праворуч на dpM-1 позицій, тобто на кількість позицій, швидше за все більше одиниці. Якщо символ, який не збігся, тексту в слові взагалі не зустрічається, то зсув стає навіть більшим, а саме зсовувати можна на довжину всього слова. Хешування даних.
|
||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 409; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.227.72.27 (0.006 с.) |

 , якщо враховувати тільки операції порівняння. Але сортування вимагає ще й в середньому
, якщо враховувати тільки операції порівняння. Але сортування вимагає ще й в середньому  переміщень, що робить її в такому варіанті значне менш ефективною, ніж сортування вибіркою.
переміщень, що робить її в такому варіанті значне менш ефективною, ніж сортування вибіркою.
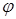 , що має властивість:
, що має властивість:
 і є золотим перерізом.
і є золотим перерізом.


