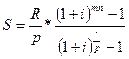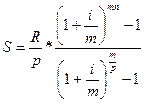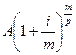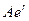Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Номинальная ставка процента - это текущая рыночная ставка, не учитывающая уровень инфляции.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Реальная ставка процента - это номинальная ставка за вычетом ожидаемых (предполагаемых) темпов инфляции. Например, номинальная годовая ставка процента составляет 11%, ожидаемый темп инфляции 8 % в год, реальная ставка процента составит (11 - 8) = 3%. Различие между номинальной и реальной процентной ставкой приобретает смысл только в условиях инфляции (повышения общего уровня цен) или дефляции (снижения общего уровня цен). Так, например, возможен такой вариант представления кредита, когда банк получает проценты сразу при выдаче кредита, т.е. сумма займа выдается с дисконтом. Дисконт в данном случае представляет собой разницу между суммой, обозначенной заемщиком в заявке, и суммой, выданной банком. Реальная или эффективная ставка процентов измеряет ту доходность, которую банк получает в целом за год с учетом дополнительных условий предоставления кредита. Сумма кредита, выдаваемая заемщику, при авансовых процентах зависит от требуемой клиенту суммы и номинальной процентной ставки и определяется из отношения:
Сумма кредита = Требуемая заемщику сумма / (1,0 – Номинальная ставка)
Очень часто при выдаче кредита банки требуют от клиента поддерживать на депозитном счете компенсационный (не снижающийся) остаток, равный определенному проценту от выданной клиенту ссуды. Размер компенсационного остатка, как правило, указывается в процентах от суммы кредита. Реальная ставка = Номинальная процентная ставка / (1,0 – Доля компенсационного остатка)
Формула наращенной суммы связывает функциональной зависимостью четыре параметра: 1) первоначальную сумму долга или вклада; 2) срок долга или вклада; 3) процентную ставку; 4) наращенную сумму.
В практике определения суммы процентных денег используется и такой вариант, когда база для начисления процентов не остается постоянной, а увеличивается с течением времени. Такая ситуация имеет место в связи с капитализацией процентов, т.е. в том случае, когда проценты не выплачиваются сразу после их начисления, а присоединяются к основной сумме долга и на вновь полученную сумму начисляются проценты. В таком случае проценты за весь период начисляются по постоянной сложной ставке. На основании сопоставления наращенных сумм при использовании простых и сложных процентных ставок можно сделать следующие выводы: 1) при одинаковой величине процентной ставки расхождение в размере множителя наращения возрастает с увеличением продолжительности периода пользования ссудой. Таким образом, при краткосрочном кредитовании банку или другому кредитору более выгодно использовать простые процентные ставки, так как возрастает величина процентного дохода. 2) при одинаковом периоде кредитования величина множители наращения зависит от вида и размера процентной ставки. Чем больше процентная ставка, тем больше выгоды кредитору приносит использование сложных процентных ставок. При долгосрочных кредитных операциях также возможно требование к клиенту о наличии компенсационного остатка и удержания комиссионных. Сложную процентную ставку банки, как правило, используют при долгосрочных операциях. В табл.1 представлены формулы финансовых расчетов при использовании простой и сложной процентных ставок.
Таблица 1. Формулы финансовых расчетов
Учетные ставки широко используются банками при операциях с денежными обязательствами (векселями). Вексель простой - безусловное долговое обязательство установленной формы, выражающее обязательство векселедателя уплатить определенную денежную сумму кредитору (векселедержателю) в определенный срок и в определенном месте. Простой вексель выписывается заемщиком. Владелец векселя с помощью его учета может получить деньги ранее указанного в векселе срока, но в размере меньше той суммы, которая указана на нем, т.е. владелец векселя реализует его с дисконтом. Дисконтом называется разность между номинальной стоимостью долгового обязательства и суммой, полученной владельцем векселя в результате его учета в финансовом учреждении. В этом случае базой начисления процентных денег является сумма погашения долга, т.е. по существу наращенная сумма S. Величина дисконта D за год будет равна произведению Sd, а за п периодов величине Snd, где d - учетная ставка. Учетная ставка равна отношению дисконта к наращенной сумме, т.е. d = (S - Р) / S. Тогда формула для расчета величины Р будет записана так:
Р= S - D = S – Snd = S* (1 - nd),
где n - продолжительность срока в годах от момента учета до даты уплаты по векселю, т.е. срок, фактически оставшийся до погашения векселя на момент его приобретения. В этой формуле величину (1 - nd)называют дисконтным множителем. В данном случае речь идет уже не о математическом, а о банковском дисконтировании. Процесс дисконтирования имеет место и тогда, когда проценты с наращенной суммы S удерживают непосредственно при выдаче ссуды (авансовые проценты).
Поскольку покупательная способность денег снижается в условиях инфляции, происходит обесценивание денежных доходов. Поэтому при помещении денег на депозит вкладчик должен сопоставит номинальную процентную ставку по депозиту с величиной индекса потребительских цен. Аналогичная проблема возникает у банка при оценке доходов от кредитной операции. При выдаче кредитов банк стремится обеспечить реальную доходность своих активных операций. Обозначим Наращенная сумма за год при отсутствии инфляции составляет величину:
S = Р(1 + i).
Эквивалент этой суммы в условиях инфляции (S/) составит:
Величину S/ можно представить, использовав в множителе наращения процентную ставку, учитывающую инфляцию, т.е. Приравняв два возможных представления У, получим:
откуда
Формула наглядно демонстрирует влияние инфляции на номинальную ставку процентов: при одном и том же уровне реальной доходности для банка номинальная ставка будет тем больше, чем выше уровень инфляции. Пусть требуемая банку доходность по кредитной операции, измеряемая простой процентной ставкой, составляет 10%, а уровень инфляции - 12% в год. Тогда при заключении кредитного соглашения банк должен учесть инфляционную составляющую. Чтобы обеспечить реальную доходность 10% по кредиту, выдаваемому на год, номинальная ставка в условиях двенадцатипроцентной инфляции должна составить:
i' = 0,10 + 0,12 + 0,10 * 0,12 = 0,232, т.е. 23,2%.
Наращенная сумма за год в условиях инфляции составит:
где i – реальная доходность по данному кредиту; τ – уровень инфляции за весь срок, на который предоставлен кредит. Учет инфляции необходим не только для расчета реальной процентной ставки, но и для определения реального дохода в результате финансовой операции. Если на определенный период динамика цен характеризуется индексом потребительских цен, то реальная наращенная сумма, оценивающая покупательскую способность денег. Таким образом, если темп прироста цен (инфляция) равен процентной ставке, то реального наращения первоначальной суммы не произойдет, а в случае если инфляция больше процентной ставки, то реальная наращенная сумма может оказаться меньше первоначальной.
Ситуационные задачи для самостоятельного решения
1. Какую сумму необходимо положить в банк на 128 дней под 7% годовых, чтобы получить 80 тыс. руб.? 2. Депозит в 500 дол. открыт на три года под 5% годовых (ставка простая процентная). В конце второго года банк увеличивает процентную ставку для сберегательных счетов до 6%. Какая сумма будет получена клиентом через три года: а) если ставка по депозиту фиксированная; б) если ставка по депозиту меняющаяся? 3. Рассчитайте величину процентов по кредиту размером 50 тыс. руб. сроком на полгода, если процентная ставка составляет 18% и а) проценты простые; б) проценты начисляются ежеквартально. 4. Заемщику для приобретения оборудования требуется иметь в наличии 50 тыс. евро, для чего он оформляет в банке кредит на год. Банк предоставляет кредит под 12%, взимая авансовые проценты. Чему равна сумма процентов и сумма кредита? 5. В банк был помещен капитал под 12% годовых. По истечении 240 дней его величина составила 575 тыс. руб. Определите величину помещенного в банк капитала и сумму начисленных процентов (расчет произвести по методу 365/365). 6. Клиент обратился в банк за кредитом в сумме 800 тыс. руб. на срок 90 дней. Банк согласен предоставить кредит по простой процентной ставке 20% годовых. Определите сумму, подлежащую возврату. 7. Если коэффициент дисконтирования для одного года равен 0,88, то чему равна процентная ставка, на основе которой рассчитан коэффициент дисконтирования? 8. В момент открытия депозита была внесена сумма 1250 евро. Через полгода на счете было 1280 евро. Чему равен коэффициент дисконтирования и величина процентной ставки? 9. Фирма планирует получение кредита на сумму 2 млн. руб. На какой срок фирма может взять кредит с тем, чтобы подлежащая возврату сумма не превысила 2,1 млн. руб.? Банк использует простую процентную ставку - 20% годовых. 10. Клиент открыл депозит в размере 1500 евро сроком на два годовой процентной ставке 6%. В конце первого года банк поднимает процентную ставку по депозитам до 6,5%. Какая сумма будет на депозите через два года? 11. Фирма приобретает оборудование стоимостью 2,5 млн. руб. и обращается в банк с целью получения кредита на эту сумму сроком на 8 месяцев. Банк предлагает два варианта представления кредита: 1) номинальная процентная ставка 16%, погашение основной суммы долга и процентов по нему в конце срока, комиссионные составляют суммы кредита; 2) номинальная процентная ставка 15%, проценты авансовые, а остальная сумма долга погашается в конце срока. Сравните реальную доходность банка по двум предложенным вариантам. Какой вариант выгоднее заемщику и почему? 12. Через 120 дней с момента подписания кредитного договора заемщик должен вернуть 750 тыс. руб. Процентная ставка по кредиту составляет 18%. Чему равна первоначальная сумма долга? 13. Под какую процентную ставку был выдан кредит размером 800 тыс. руб. на срок 200 дней, если наращенная сумма составила 865,75 тыс. руб.? 14. Чему равен коэффициент наращения и сумма процента если кредит был выдан на срок три месяца в размере 120 тыс. руб., а заемщик обязан вернуть 132 тыс. руб.? 15. Кредит на сумму 30 тыс. евро выдан на два года. Какую сумму должен вернуть заемщик, если процентная ставка по кредиту была установлена в размере 12%? 16. Депозит в размере 400 тыс. руб. был открыт на три года. По окончании срока депозита клиент получил 532,4 тыс. руб. Чему равна сложная процентная ставка по депозиту? 17. Депозит размером 500 тыс. руб. открыт на два года. Какая сумма будет возвращена клиенту, если по сложной процентной ставке по депозиту начислялось 10%? Какова будет реальная покупательская способность денег, полученных клиентом, если уровень инфляции ставил в первый год 11,5%; во второй год 9,5%? 18. Сравните суммы процентов по кредиту в 1 млн. руб. на срок четыре месяца в двух банках, если известно, что в первом банке проценты начисляются ежемесячно, а во втором - идет непрерывное начисление процентов. Номинальная процентная ставка по кредиту одинаковая в двух банках и составляет 18%. 19. Депозит в размере 350 тыс. руб. открыт на два года. Начисление сложных процентов осуществляется по процентной ставке в следующем размере: в первый год - 8%; во второй год - 8,5%. Определите сумму на депозите через два года и размер процентов, полученных вкладчиком. 20. Ссуда в размере 400 тыс. руб. выдана на полгода. Сравните результаты наращения при номинальной ставке 18%, если проценты начисляются: а) по простой процентной ставке; б) по сложной процентной ставке. 21. Определите сложную процентную ставку по кредиту размере 12 млн.руб. на срок два года, если заемщик при единовременном погашении основного долга и процентов по нему выплатил банку 1 млн. 699 тыс. руб. 22. На какую сумму следует открыть депозит, чтобы через полтора года счете вкладчика было 400 тыс. руб., если банк предлагает по депозитам на этот срок сложную процентную ставку 10% годовых? 23. Банк стремится обеспечить реальную доходность по краткосрочным рублевым кредитам в размере 4%. Какой должна быть номинальная ставка по кредиту, выдаваемому на год, если инфляции составляет 11%?
МОДЕЛИ ФИНАНСОВЫХ ПОТОКОВ
В настоящее время функционирование хозяйствующих субъектов среднего размера осложняется, с одной стороны, усилением конкуренции со стороны крупных организаций. С другой стороны, выросли потребности рынка покупателей, изменилось их отношение к качеству и цене товаров, продуктов и услуг. В таких условиях первые вынуждены искать новые, неценовые, формы эффективной конкуренции, связанные с качеством обслуживания, отраслевой специализацией, использованием новых технологий и т. д. Вполне очевидно, что финансовое благополучие любой коммерческой структуры непосредственно связано с устойчивостью получения доходов. В этой связи неизбежно усиливается внимание к доходам, получаемым от управления активами и пассивами. В сложившихся условиях выживаемость средних коммерческих структур связана с получением ими конкурентных преимуществ путем создания сбалансированной системы управления финансовыми потоками. Экономическая эффективность деятельности организации основывается на наличии удачной рыночной стратегии, максимально полного и эффективного использования финансовых ресурсов, минимизации комплекса рисков. Все эти задачи и призвана решить система управления финансовыми потоками, базирующаяся на своевременном получении и анализе аналитической информации и принятии адекватных управленческих решений. На современном этапе развития экономики России одной из важнейших проблем, стоящих перед отечественными компаниями, является проблема эффективного и гибкого механизма управления финансовыми потоками. В современной отечественной экономике наличие необходимого уровня прибыльности компании не всегда является залогом ее успешного развития. Отсутствие достаточного объема оборотных средств и эффективного управления финансовыми потоками приводят к ухудшению финансовой устойчивости, снижению деловой активности, что, в свою очередь, может стать предпосылкой серьезного финансового кризиса хозяйствующего субъекта. Эффективное и рациональное управление потоками денежных средств и их эквивалентов способствует достижению финансовой устойчивости, прибыльности и положительной динамики развития компании. В условиях постоянно изменяющейся экономической ситуации достижение данной цели невозможно без использования теоретических подходов и практических разработок в области управления финансовыми потоками. Непрерывный процесс движения денежных средств во времени представляет собой денежный поток. Это понятие является агрегированным, включает в себя различные виды денежных потоков, обслуживающих хозяйственную деятельность. Как правило, финансовая деятельность предприятий характеризуется множеством распределенных во времени платежей и поступлений денежных средств. К таким финансовым операциям относят оплату поставщикам за приобретаемое сырье, материалы, топливо, электроэнергию, выплату налогов, расходы на оплату труда работников, выплату дивидендов, поступление денежных средств за поставленную потребителям продукцию и услуги, продажу имущества и др. Аналогичным образом можно рассмотреть поступление и расходы денежных средств у физических лиц: оплата жилищно-коммунальных услуг, расходы на образование, медицинское обслуживание и т.д., получение заработной платы, процентов по вкладам и дивидендов по акциям и др. Последовательный ряд выплат называют потоком платежей. В целом ряде случаев платежи осуществляются через равные промежутки времени. Например, ежемесячное погашение основного долга и процентов по нему, выплата процентов по облигациям, оплата за тепло-и электроэнергию и др. Серию периодических платежей в установленные сроки за определенный период времени называют финансовой рентой, и ли аннуитетом.
Ренты различаются между собой по ряду признаков: - по продолжительности периода ренты (интервала времени между последовательными платежами) выделяют ренты годовые и р -срочные (р - число платежей в году); - по числу отдельных платежей различают ренты с конечным числом платежей и бесконечные (вечные ренты); - по размерам платежей ренты могут быть с постоянными (равными) платежами и с переменными (неравными) платежами; - по моменту выплат различают обычные ренты (ренты постнумерандо) и ренты пренумерандо. Если платежи осуществляются в конце периода, то такую ренту называют обычной, или рентой постнумерандо; если же выплаты производятся в начале каждого периода, то ренту называют пренумерандо. Наиболее распространенными являются обычные ренты (ренты постнумерандо); - числу раз начисления процентов в году. Начисление процентов может производиться один раз в год или несколько раз в год (т раз). В практической деятельности зарубежных и российских банков часто число платежей в году по основной сумме долга равно числу начислений процентов в течение года, т.е. т = р. Общим для всех финансовых рент свойством является равенство интервалов времени, через которые производятся платежи. В количественном анализе финансовых рент обычно решаются следующие задачи: 1) характеристика будущей стоимости (наращенной суммы) всех выплат с начисленными на них процентами. Наращенная сумма определяется, например, при оценке накопленной задолженности, при определении суммы на депозите по окончании срока ренты и др.; 2) оценка современной (приведенной) стоимости всех выплат на протяжении срока ренты. Необходимость определения современной стоимости возникает в анализе инвестиционных проектов, разработке плана погашения кредита, определении текущей стоимости облигаций и др. Для решения двух сформулированных выше задач анализа финансовой ренты необходимо знать следующие основные параметры: 1) величину каждого отдельного платежа; 2) срок ренты, т.е. время от начала финансовой ренты до конца последнего ее периода; 3) процентную ставку, используемую при наращении или дисконтировании платежей; 4) период ренты, который представляет собой временной интервал между двумя последовательными платежами. К числу дополнительных условий, определяющих величину будущей стоимости ренты, относится также число платежей в году, число раз начислений процентов в году и момент платежа. Будущая стоимость (наращенная сумма) всего потока платежей определяется суммированием будущей стоимости каждой выплаты. Рассмотрим определение наращенной суммы для постоянных годовых и р -срочных рент. Для определения величины наращенной суммы постоянной финансовой ренты необходимо знать следующие основные параметры: 1) величину годового платежа; 2) срок ренты; 3) процентную ставку, используемую при наращении платежей; 4) период ренты. В табл. 2 приведены формулы для определения наращенной стоимости постоянной финансовой ренты для различных сочетаний таких дополнительных условий, как число платежей в году, количество раз начислений процентов в году, момент платежа. Обозначения: R - годовой платеж; i - годовая процентная ставка; n - срок ренты; p - количество равных платежей в году; m - количество раз начислений процентов в году; r - непрерывная процентная ставка. Таблица 2. Формулы для определения стоимости финансовой ренты
Дисконтирование денежных потоков - это приведение стоимости потоков платежей, выполненных в разные моменты времени, к стоимости на текущий момент времени. Это делается, например, при экономической оценке эффективности инвестиций или при оценке бизнеса. Дисконтирование отражает тот экономический факт, что сумма денег, которой мы располагаем в настоящий момент, имеет б о льшую реальную стоимость, чем равная ей сумма, которая появится в будущем. Это обусловлено несколькими причинами, например: Имеющаяся сумма может принести прибыль, например, будучи положена на депозит в банке. Покупательная способность имеющейся суммы будет уменьшаться из-за инфляции. Всегда есть риск неполучения предполагаемой суммы. Очень часто в контрактах финансового характера предусматривают не отдельные разовые платежи, а серию платежей, распределенных во времени. Примерами могут быть регулярные выплаты с целью погашения долгосрочного кредита вместе с начисленными на него процентами, периодические взносы на расчетный счет, на котором формируется некоторый фонд различного назначения (инвестиционный, пенсионный, страховой, резервный, накопительный и т.д.), дивиденды, выплачиваемые по ценным бумагам, выплаты пенсий из пенсионного фонда и пр. Ряд последовательных выплат и поступлений называют потоком платежей. Выплаты представляются отрицательными величинами, а поступления - положительными. Обобщающими характеристиками потока платежей являются наращенная сумма и современная величина. Каждая из этих характеристик является числом.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-15; просмотров: 2089; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.181.250 (0.016 с.) |




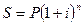
 *…
*… 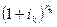

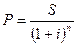




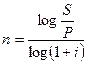


 уровень инфляции, выраженный в долях единицы. Если известен индекс потребительских цен
уровень инфляции, выраженный в долях единицы. Если известен индекс потребительских цен  , то
, то  . При выдаче кредитов банк стремится обеспечить реальную доходность своих активных операций.
. При выдаче кредитов банк стремится обеспечить реальную доходность своих активных операций. .
. , где
, где  - процентная ставка, обеспечивающая требуемую эффективность кредитной операции при уровне инфляции
- процентная ставка, обеспечивающая требуемую эффективность кредитной операции при уровне инфляции 
 .
. ,
,