
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
В13 Модели межотраслевого баланса. Межотраслевой баланс в стоимостной формеСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Имеется n отраслей производства. Согласно статистическим данным известно, сколько продукции каждой отрасли используется в других отраслях в качестве исходных материалов или комплектующих, а также, сколько этой продукции остается для конечного использования. Все эти данные записываются в виде таблицы, в которой: – каждая строка таблицы соответствует одной из отраслей, выступающей как производитель определенного вида продукции. Для простоты предполагается, что каждая отрасль производит только один вид продукции. – первые n столбцов таблицы соответствуют тем же отраслям, которые теперь уже выступают в роли потребителей продукции других отраслей, используемой для организации своего производства (промежуточное потребление); – в предпоследнем столбце таблицы содержится информация о той части продукции отрасли, которая осталась для конечного использования; – в последнем столбце таблицы записывается общий объем всей про- изведенной отраслью продукции (валовой объем), равный сумме промежуточного и конечного потребления. В каждой отрасли кроме сырья и исходных материалов для организации производства расходуются и другие ресурсы: изнашивается оборудование, оплачивается труд работников, делаются налоговые отчисления. Все эти и некоторые другие расходы (к которым относят и прибыль, и полученные субсидии (со знаком минус)) образуют добавленную стоимость, которая обычно выражается в общих для всех отраслей денежных единицах. Причину отнесения прибыли к расходам можно прокомментировать следующим образом. По известной формуле Следовательно, наше предположение о том, что прибыль входит одним из слагаемых в расходы не нарушает основного баланса.
Добавленная стоимость компенсируется производителям путем оплаты потребителями стоимости продукции по определенным ценам. Поскольку здесь имеется ввиду только конечный спрос, то суммарную добавленную стоимость L записывают не в последний столбец (в который записывалась сумма по всем предыдущим строкам), а в столбец конечного спроса. Зная величину Обозначим через Оказывается, если добавленная стоимость во всех отраслях известна, то величины Действительно, сумма доходов i-й отрасли, полученных от промежуточного и конечного использования ее продукции, равна
В матричном виде эти равенства можно записать в виде:
Если вектор l считается известным, вектор стоимостей p можно найти по формуле:
Матрица Из формулы (15.1) получим, что
Таким образом, совокупная добавленная стоимость равна совокупному конечному спросу в стоимостной форме. Для таблицы 15.1 это означает, что L является не только суммой всех чисел в строке добавленной стоимости, но и суммой всех чисел в столбце конечного спроса. Формально баланс в стоимостной форме отличается от баланса в натуральном выражении только тем, что в первом случае все данные в балансе выражаются в одних и тех же единицах измерения, тогда как во втором случае в каждой строке баланса может быть своя единица измерения количества продукции. Поэтому над данными баланса в стоимостной форме мы можем совершать те же операции, что и над данными баланса в натуральной форме. Пусть Тогда элементы матрицы прямых производственных затрат в стоимостной форме будут вычисляться по формуле: Определим В частности, если предположить, что во всех отраслях есть дополни- тельные расходы, т.е. все Рассмотренная модель межотраслевого баланса носит название модели Леонтьева.
|
||||
|
Последнее изменение этой страницы: 2016-07-14; просмотров: 430; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.10.75 (0.008 с.) |

 получаем, что
получаем, что 

 добавленной стоимости в j-й отрасли, определим
добавленной стоимости в j-й отрасли, определим  – добавленную стоимость единицы продукции
– добавленную стоимость единицы продукции  измеряется в денежных единицах за единицу продукции j -й отрасли).
измеряется в денежных единицах за единицу продукции j -й отрасли). стоимость продукции в i-й отрасли. Умножив данные в i-й строке на соответствующую стоимость
стоимость продукции в i-й отрасли. Умножив данные в i-й строке на соответствующую стоимость  получим баланс в стоимостной форме (все данные в этой таблице 15.2 выражаются в общей для всех отраслей денежной форме):
получим баланс в стоимостной форме (все данные в этой таблице 15.2 выражаются в общей для всех отраслей денежной форме): определяются однозначно (исходя из требования о равенстве доходов и расходов всех отраслей).
определяются однозначно (исходя из требования о равенстве доходов и расходов всех отраслей). Расходы этой же отрасли можно вычислить, найдя сумму по j-му столбцу таблицы 15.1. Приравняем найденные величины (напомним, что прибыль учитывается в числе расходов в составе добавленной стоимости). Получим:
Расходы этой же отрасли можно вычислить, найдя сумму по j-му столбцу таблицы 15.1. Приравняем найденные величины (напомним, что прибыль учитывается в числе расходов в составе добавленной стоимости). Получим:



 получается из матрицы
получается из матрицы  транспонированием, поэтому обратные матрицы для них существуют одновременно и если
транспонированием, поэтому обратные матрицы для них существуют одновременно и если 
 следовательно,
следовательно,
 – валовый выпуск в i-й отрасли в стоимостной форме;
– валовый выпуск в i-й отрасли в стоимостной форме;  – объем конечного потребления в i -й отрасли в стоимостной форме;
– объем конечного потребления в i -й отрасли в стоимостной форме;  – объем продукции i -й отрасли, использованной в j –й отрасли, в стоимостной форме.
– объем продукции i -й отрасли, использованной в j –й отрасли, в стоимостной форме.
 – добавленную стоимость единицы (в стоимостном смысле) продукции j-й отрасли. Аналогично формуле (13.1) получаем:
– добавленную стоимость единицы (в стоимостном смысле) продукции j-й отрасли. Аналогично формуле (13.1) получаем: 
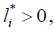 то получаем, что
то получаем, что 



