В8 Модели теории игр. Осн. понятия теории игр. Решение матричных игр в чистых стратегиях

Игра - упрощенная модель конфликтной ситуации. Игра ведется по определенным правилам. Суть игры в том, что каждый из ее участников принимает такие решения, которые, как он полагает, могут обеспечить ему наилучший результат (исход). Исход игры – это значение некоторой функции, называемой функцией выигрыша (платежной функцией). Эта функция задается либо таблицей, либо аналитическим выражением. Если сумма выигрышей игроков равна нулю, то игру называют игрой с нулевой суммой. Если в игре участвуют 2 игрока, то ее называют парной. В качестве игрока может выступать как отдельное лицо, так и группа лиц, объединенных общей целью. Каждый игрок в ходе развивающейся конфликтной ситуации выбирает образ своих действий самостоятельно, имея лишь общее представление о множестве допустимых ответных решений партнера. Поэтому ни 1 из игроков не может полностью контролировать положение, так что как одному и другому игроку решение приходится принимать в условиях неопределенности. Непременным остается только стремление игроков использовать любую ошибку партнера в своих интересах. Игры, в которых оба участника, действуя в строгом соответствии с правилами, в равной мере сознательно стремятся добиться наилучшего для себя результата, наз-т стратегическими.

В экон. практике приходится моделировать ситуации, придавая им игровую схему, в которых один из участников безразличен к рез-ту игры. Такие игры наз-т играми с природой, понимая под термином "природа" всю совокупность внешних обстоятельств, в которых сознательному игроку приходится принимать решение. В играх с природой степень неопределенности при принятии решения сознательным игроком возрастает. Объясняется это тем, что если в стратегических играх каждый из участников постоянно ожидает наихудшего для себя ответного действия партнера.

Пусть игроки и располагают конечным числом возможных действий – чистых стратегий. Обозначим их соответственно А_1..,А_m и В_1.., Вn. Игрок А может выбирать любую чистую стратегию А_i (i=1,m), в ответ на которую игрок B может выбрать любую свою чистую стратегию B_j (j=1,n). Если игра состоит только из личных ходов пары стратегий (A_i,B_j) однозначно определяет результат a_ij – выигрыш игрока A. При этом проигрыш игрока B составляет a_ij. Если известны значения a_ij – вы-

игрыша для каждой пары (A_i,B_j) чистых стратегий, можно составить матрицу выигрышей игрока A (проигрышей игрока B) (табл.1). Ее наз-т платежной.

Таб.1

 

В таб.1 приведены числа a_i – минимально возможный выигрыш игрока A, применяющего стратегию А_i (i=1,m), B_J= max a_ij – максимально возможный проигрыш игрока B, если он пользуется стратегией B_j (j=1,n).

Число наз-т нижней чистой ценой игры (максимином), а соответствующую ему чистую стратегию –A⁰_i – максиминной. Число 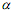показывает, какой минимальный гарантированный выигрыш может получить игрок A, правильно применяя свои чистые стратегии при любых действиях игрока B. Число наз- т верхней чистой ценой игры (минимаксом), а соответствующую чистую стратегию B⁰_j – минимаксной. Число 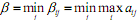показывает, какой минимальный гарантированный проигрыш может быть у игрока B при правильном выборе им своих чистых стратегий независимо от действий игрока A. Т.О., правильно используя свои чистые стратегии, игрок A обеспечит себе выигрыш не меньше, а игрок B в результате правильного применения своих чистых стратегий не позволит игроку A выиграть больше, чем 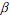. Ясно, что 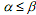. Если 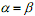, то говорят, что игра имеет седловую точку в чистых стратегиях и чистую цену игры . Пару чистых стратегий A_i и B_j,соответствующих 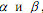, наз-т седловой точкой матричной игры, а элемент 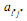платежной матрицы, стоящий на пересечении 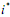-й строки и 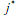-гo столбца, – седловым элементом платежной матрицы. Он одновременно является минимальным в своей строке и максимальным в своем столбце, т.е. 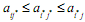. Стратегии 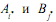, образующие седловую точку, являются оптимальными. Тройку наз-т решением игры. Для игр без седловых точек оптимальные стратегии игроков находятся в области смешанных стратегий.