
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Система аксіом евклідової геометрії Г.Вейля.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
В останні десятиріччя при розгляданні питань пов’язаних з обґрунтуванням геометрії все більшу перевагу надають аксіоматиці Вейля. Цю аксіоматику називають також точково-векторною, оскільки в ній основними неозначуваними поняттями є точки і вектори. Система аксіом Вейля описує основні шість понять, два з яких – точки і вектори – називаються основними об’єктами. Поняття «додавання векторів», «множення вектора на число», «скалярний добуток векторів» і «відкладання вектора від точки» називаються основними відношеннями. Аксіоми Вейля розподіляються на п’ять груп. Причому аксіоми перших трьох і перших чотирьох груп складають відповідно аксіоматику афінного і евклідового простору. Сукупності усіх точок і векторів позначаються відповідно символами АКСІОМИ ДОДАВАННЯ ВЕКТОРІВ Перша група аксіом описує відображення j1: Операція додавання векторів задовольняє наступним аксіомам: 1/ Додавання векторів комутативне: для довільних двох векторів
2/ Додавання векторів асоціативне: для " трьох векторів ( (( 3/ Існує такий вектор (для " 4/ Для " вектора (для " Вектор 1.2 АКСІОМИ МНОЖЕННЯ ВЕКТОРА НА ДІЙСНЕ ЧИСЛО Друга група аксіом описує відображення j2: 1/ Операція j2 дистрибутивна відносно додавання векторів: для " векторів l( (для " 2/ Операція j2 дистрибутивна відносно додавання чисел: для " вектора (l+m) (для " 3/ Операція асоціативна: для довільного вектора (для " 4/ Операція множення вектора 1´ Аксіоми 1-2 дозволяють визначити поняття векторного простору. Векторним простором над полем дійсних чисел Векторний простір є математичною структурою ( Нагадаємо поняття ізоморфізму векторних просторів
" двох векторів
Із означення випливає, що 1/ тотожне відображення Перш ніж перейти до формулювання аксіом розмірності нагадаємо ряд понять із курсу алгебри. Система векторів Вектор l1 У випадку лінійної залежності системи векторів x1,x2,...,xk нульовий вектор може бути представлений у вигляді нетривіальної комбінації векто-рів, у випадку ж лінійної незалежності - тільки у вигляді тривіальної. АКСІОМИ РОЗМІРНОСТІ. 1. Існують три лінійно незалежних вектори l1 2. Будь-які чотири вектори (для довільних (l1 ( Аксіоми 1-3 дозволяють ввести поняття тривимірного простору. Векторний простір Щоб одержати аксіоматику n-вимірного векторного простору над полем 1´. Існує n лінійно незалежних векторів: 2´. Будь-яка система. що містить n+1 вектор лінійно залежна. Множина Кожна система n лінійно незалежних векторів простору 1.4 АКСІОМИ СКАЛЯРНОГО ДОБУТКУ ВЕКТОРІВ. Четверта група аксіом описує відображення j3: 2/ Скалярний добуток векторів лінійний: для " трьох векторів дійсних чисел l,m виконується рівність ( (для " (" Аксіоми груп 1-4 дозволяють ввести поняття евклідового векторного простору і ізоморфізму таких просторів. Векторний простір Два евклідові векторні простори що зберігає операцію скалярного множення векторів. Якщо Відмітимо, що евклідів векторний простір є структурою ( ____ |
cos j= ¾¾¾¾¾. |
Із курсу алгебри відомо, що для " |
Скалярний добуток двох векторів x,y, скалярний квадрат вектора і ко-синус кута між двома векторами в ортонормованому базисі виражаються відповідно формулами:
cos j= ¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾, (1.6) √
де
1.5 АКСІОМИ ВІДКЛАДАННЯ ВЕКТОРІВ. Ця група аксіом описує операцію відкладання векторів j4: Операція відкладання j4 визначається слідуючими аксіомами: 1/ для кожної фіксованої точки А Є
мал. 1
2/ Для " трьох точок
|
||||
|
Последнее изменение этой страницы: 2016-07-11; просмотров: 622; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.172.190 (0.008 с.) |

 і
і 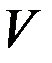 .
. ,
,  третій вектор j1(
третій вектор j1( справедлива рівність:
справедлива рівність: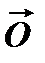 , що для " вектора
, що для " вектора  ) (
) ( ®
®  векторного простору V на векторний простір
векторного простору V на векторний простір 1,
1, 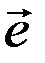 2,
2,  3:
3: ,
,  ,
,  ,
, 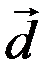 лінійно залежні:
лінійно залежні: ),
), ¹
¹  1,
1,  1
1  1+
1+  ,
,  Є
Є  , де
, де  справедлива рівність
справедлива рівність  =
=  (аксіома трикутника) (мал.2).
(аксіома трикутника) (мал.2).


