
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теорема про існування та єдиність площі многокутника
Визначимо площу многокутника, таким чином: S= де O-будь-яка точка в площині многокутника. Теорема 1.2.6. (Про існування і єдиність площі многокутника) Для множини многокутників М і множини дійсних додатних R+ чисел існує єдине відображення S:M®R+, за допомогою якого будь-якому многокутнику можна поставити у відповідність число S=1/2 × яке задовольнятиме аксіомам вимірювання площ. Доведення. І.Покажемо, що коли ми задамо відображення S множини многокутників на множину дійсних додатних чисел, задане формулою (1.2.7), то воно буде задовольняти трьом метричним аксіомам вимірювання площ. 1. Нехай маємо два конгруентні многокутники М1 і М2: М1 Завжди існує рух, за допомогою якого ми можемо відобразити многокутник М1 на многокутник М2 d(M1)=M2, В силу збереження скалярних добутків маємо право стверджувати, що буде виконуватись рівність: S(M1)=S(M2). 2. Доведемо, що також буде виконуватись аксіома 2. Якщо многокутник розбити ламаною на складові частини,то S(M)=S(M1)+S(M2). В правій частині цієї рівності деякі доданки будуть повторювати доданки з суми S(M), але з'являться нові доданки за допомогою ортів ламаної поділу. Суми S(M1) i S(M2) будуть повторювати доданки з суми S(M) i до них додаються доданки: добутки відрізків ламаної на відповідні орти. Орти зовнішніх нормалей для ланок ламаної будуть взаємно протилежними векторами, отже числа, що представляють собою добутки відрізків ламаної на відповідні орти, в сумі дорівнюють нулю. Таким чином, S(M)=S(M1)+S(M2).
3. Нехай візьмемо квадрат із стороною, рівною 1. Точка О співпадає з центром квадрата, точки Мі - середини сторін. Позначимо через Si=
Отже, Si=1/2
Таких чисел Si буде 4. Значить, число S=1/2×4×1/2=1. Таким чином, аксіома 3 виконується. Відображення S задовольняє метричним аксіомам вимірювання площ многокутників. ІІ. Покажемо, що це відображення єдине. Доведення проведемо методом від супротивного. Припустимо, що таких відображень існує два: нехай це S i K. Коли задано будь-який многокутник М, ми можемо розбити його на скінченну кількість трикутників: S(M)= Оскільки раніше було доведено, що при існуванні відображення S площа будь-якого трикутника дорівнює 1/2 добутку основи на висоту, то користуючись цим і порівнюючи дві рівності (1.2.8), можна стверджувати, що праві частини рівні. Отже, рівні і ліві частини, тобто S(M)=K(M). Звідси випливає, що відображення S єдине.
Означення та властивості рівновеликих і рівноскладених многокутників. Означення. Два многокутники, які мають рівні площі, називаються рівновеликими. Означення. Два многокутники називаються рівноскладеними, якщо їх можна розкласти на однакову кількість попарно конгруентних многокутників. Твердження 2.1.1. Поняття рівновеликості многокутників є відношенням еквівалентності. 1. S(M)=S(M). 2. S(M1)=S(M2) => S(M2)=S(M1). 3. S(M1)=S(M2), S(M2)=S(M3) => S(M1)=S(M3). Всі аксіоми виконуються, оскільки вони мають місце для дійсних додатніх чисел. Наслідок. Якщо маємо два многокутники М1 і М2, які розбиті на однакову кількість попарно конгруентних трикутників, то площі многокутників рівні. S(M1)=S(M2). Твердження 2.1.2. Поняття рівноскладеності многокутників є відношенням еквівалентності. Доведення. Повинно виконуватись три умови. Позначимо через w-відношення рівноскладеності. 1. М w M - рефлексивність випливає з означення. 2. М1 w M2 => M2 w M1- симетричність слідує з означення.
3. M1 w M2, M2 w M3 => M1 w M3 -транзитивність. Доведення (транзитивності відношення рівноскладеності). Нехай М1 w М2. Це означає, що існує скінченна система многокутників m1, m2,..., mn, на які або відповідно їм конгруентні можна розкласти як многокутник М1, так і многокутник М2, тобто
Маємо, що М2 w M3. Це означає, що існує деяка відмінна від попередньої скінченна система многокутників р1, р2,..., рn, на які або відповідно їм конгруентні можна розкласти многокутники М2 і М3.
Щоб довести рівноскладеність многокутників М1wM3, нам потрібно довести існування спільної системи многокутників розкладу для многокутників М1 і М3. Нехай на многокутнику М2 нанесені обидві вище розглянуті системи розкладу:
Розглянемо перетин многокутників у різних системах. Це або порожня множина, або точка, або відрізок, або система відрізків, або многокутник. Розглянемо загальний випадок, коли в перетині ми отримали многокутник, тобто
При зміні індекса і многокутники М утворюють многокутник рj
Отримали, що М1 і М3 розбиваються на однакову кількість конгруентних многокутників. Комбінуючи розклад на многокутники одним чином, отримаємо многокутник М1, а іншим - многокутник М3. Звідси випливає, що М1 w М3.
|
||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-11; просмотров: 514; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.14.70.203 (0.018 с.) |
 i (i=1,..., к). На сторонах многокутника виберемо довільні точки М1, М2,..., Мк і при точках Мі побудуємо зовнішні перпендикуляри і орти променів [Mi Xi). Позначимо їх через
i (i=1,..., к). На сторонах многокутника виберемо довільні точки М1, М2,..., Мк і при точках Мі побудуємо зовнішні перпендикуляри і орти променів [Mi Xi). Позначимо їх через  i і назвемо
i і назвемо 



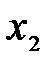








 i (
i (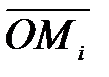 ,
,  ,
, М2, М1
М2, М1  S(M1), M2
S(M1), M2  =
=  , тобто відповідні Їх сторони конгруентні:. Рух евклідового простору завжди супроводжується векторним простором. При цьому ортогональному перетворенні образом будь-якого
, тобто відповідні Їх сторони конгруентні:. Рух евклідового простору завжди супроводжується векторним простором. При цьому ортогональному перетворенні образом будь-якого  буде
буде  , тобто d(
, тобто d( )=
)= 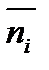 )=
)=  . Ортогональне перетворення володіє властивістю, що скалярний добуток зберігається: (
. Ортогональне перетворення володіє властивістю, що скалярний добуток зберігається: ( )=(
)=(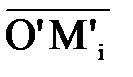 ,
,  ). Точка Мi лежить на стороні многокутника М1, точка Мi' лежить на стороні многокутника М2.
). Точка Мi лежить на стороні многокутника М1, точка Мi' лежить на стороні многокутника М2. , де
, де  =1, (
=1, (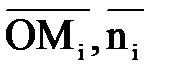 )=1/2,
)=1/2,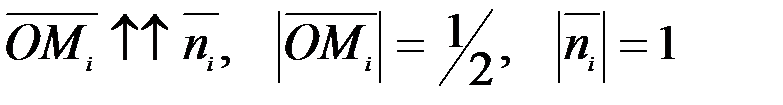 .
.
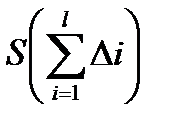 ,
, 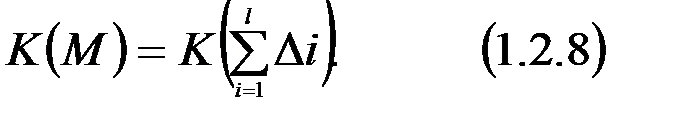 .
. (2.1.1)
(2.1.1) . (2.1.2)
. (2.1.2) . (2.1.3)
. (2.1.3) . При зміні індекса j многокутники Мij утворюють многокутник m'i, тобто
. При зміні індекса j многокутники Мij утворюють многокутник m'i, тобто
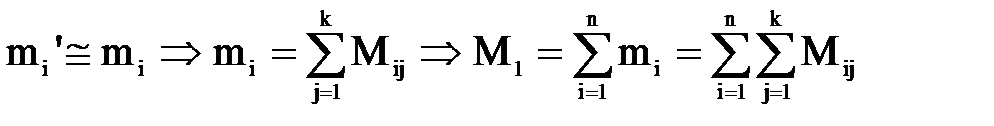 (2.1.4)
(2.1.4)
 . (2.1.5)
. (2.1.5)


